[HNOI2011]括号修复

【出处】

HNOI2011Day1

【题目描述】

给定一个长度为N的由“(”和“)”组成的字符串和M个操作。

要求实现四个操作：

1、统一：将[a,b]之间的所有括号改成c（“(”或“)”）

2、翻转：将[a,b]之间的字符串翻转

3、改变：将[a,b]之间的‘(’变成‘)’

4、询问：询问[a,b]之间的字符串至少要改变多少位才能变成合法的括号序列。

N,M≤100000

【算法分析】

此题非常巧妙，可以成功转化成类似最大连续子序列的求解方式，并运用Splay进行维护。

对于一个已知的括号，我们该如何求出询问的答案？

比如）（（（））（（这样一个，我们把符合的一层层去掉，就变成了）（（（，那么很显然答案是3。并且易得，所有的字符串化简后必是))...)((...(的形式（或全是)或(），答案就是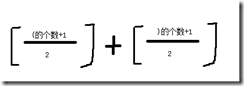。关键就是如何求出个数来。考虑左起的），我们发现，当一个字符串）））））（））中有了一个(，就相当于连续的(减少了1。如果我们把（看成+1，）看成-1，那么答案就是从最左边开始连续最小的一段。同样的从右边可算出（。即我们把原串的（看成+1，）看成-1，问题就变成了求左起连续最小一段和右起连续最大一段。

由于还涉及到修改，我们考虑用Splay动态维护，首先要维护基本的五个：father,left,right,size,s（这个元素的值）。涉及到翻转，所以我们维护四个答案需要的信息：xl,xr,yl,yr,sum，表示左起、右起最多的+1个数，左起、右起最多的-1个数，子树和，且这里xl,xr,yl,yr>=0,sum可正可负。

对于统一，记一个sa标志，表示该子树所有元素都变为这一个。

对于翻转，记一个rev标志，表示该子树是否翻转。

对于改变，记一个en标志，表示该子树是否改变。

并且三者都需要下传标记。下传时s,xl,xr,yl,yr,sum都需维护。统一比较简单，翻转要交换xl和xr，yl和yr，改变要交换xl和yl，xr和yr。而rev还需将左右子树对换（序列的顺序改变）。

每次对于提取区间(a,b)，分情况讨论。

1、整个区间——区间对应为根

2、(1,x)——x+1旋到根，区间对应为根的左子树

3、(x,n)——x-1旋到根，区间对应为根的右子树

4、(x,y)——x-1旋到根，接着y+1旋到根的右子树，区间对应为根的右子树的左子树

每次操作提取出来区间对应的子树节点后进行操作，并将到根的路径上的节点再维护一下。

问题到这似乎已经完美解决了。

但是，我们要注意到一个极其棘手的问题，如果一个节点同时存在统一，翻转，改变，先传哪一个？首先，翻转是没有问题的，先翻转再统一，或先统一再翻转都一样，先翻转再改变，或先改变再翻转也都一样，我们不妨把它的顺序放在第一位。然而先统一再改变与先改变再统一却会出问题的，两者会有不一样的结果，到底哪个在前？只能视标记的最初时间而定。统一的时间早则先统一，否则先改变。于是我们马上想到记录一个标记时间，下传时，将标记时间一同下传即可。但是这样做仍是会出问题的。为什么？

我们对一个节点（开始什么标记也没有）进行三次操作（假设中间不下传）：改变，统一，改变。那么我们会发现，原本我们记录的boolean类型的en两次操作后变成了false，而统一符号仍然在，我们下次要下传时，子树的标记就完全不对了。为什么？因为我们之前考虑的是两次改变等价于没改，但是如果中间有统一标志，那么其实就是不等价了。

解决这一问题的方法可以是，先把改变放在前，统一放在后。那么我们只需特判一种情况：先统一，再改变，而这种情况出现的条件是在先改变下传标记时，有统一标记且统一标记的时间比当前改变下传标记早，那么我们就只需将改变记为false，将统一变为其相反数，并维护即可。也即强制使统一标记的时间大于改变下传标记时间。至此问题解决的主要过程已清晰可见了。

空间复杂度O(N)。建树O(N)，单次询问O(logN)，总时间复杂度O(N+MlogN)。

 

 

 

 

 

 

const
	maxn=100000;
var
	n,m,i,j,k,p,x,y,root,tmp:longint;c:char;str:string;
	rev,en:array[0..maxn] of boolean;
	l,r,fa,sum,s,size,sa,xl,xr,yl,yr,satime,entime:array[0..maxn] of longint;
function reads:string;
begin
	reads:='';
	repeat
		read(c);
		if c=' ' then break;
		reads:=reads+c;
	until eoln;
end;

function readn:longint;
begin
	readn:=0;
	repeat
		read(c);
		if c=' ' then break;
		readn:=readn*10+ord(c)-ord('0');
	until eoln;
end;
function max(a,b:longint):longint;
begin
	if a>b then exit(a) else exit(b);
end;
procedure prev(i:longint);
begin
	rev[i]:=not rev[i];
	tmp:=xl[i];xl[i]:=xr[i];xr[i]:=tmp;
	tmp:=yl[i];yl[i]:=yr[i];yr[i]:=tmp;
	tmp:=l[i];l[i]:=r[i];r[i]:=tmp;
end;
procedure psa(i,t,time:longint);
begin
    satime[i]:=time;
    sa[i]:=t;
	s[i]:=t;
	sum[i]:=t*size[i];
	if t=1 then begin xl[i]:=sum[i];xr[i]:=sum[i];yl[i]:=0;yr[i]:=0;end
	else begin xl[i]:=0;xr[i]:=0;yl[i]:=-sum[i];yr[i]:=-sum[i];end;
end;

procedure pen(i,time:longint);
begin
	if (satime[i]>0)and(satime[i]<time) then
    begin
		en[i]:=false;
        psa(i,-sa[i],time);
        exit;
   end;

        entime[i]:=time;
        en[i]:=not en[i];
    s[i]:=-s[i];
    sum[i]:=-sum[i];
	tmp:=xl[i];xl[i]:=yl[i];yl[i]:=tmp;
	tmp:=xr[i];xr[i]:=yr[i];yr[i]:=tmp;
end;

procedure pup(i:longint);
begin
	size[i]:=size[l[i]]+size[r[i]]+1;
	sum[i]:=sum[l[i]]+sum[r[i]]+s[i];
	xl[i]:=max(max(xl[l[i]],sum[l[i]]+s[i]+xl[r[i]]),0);
	xr[i]:=max(max(xr[r[i]],sum[r[i]]+s[i]+xr[l[i]]),0);
	yl[i]:=max(max(yl[l[i]],-sum[l[i]]-s[i]+yl[r[i]]),0);
	yr[i]:=max(max(yr[r[i]],-sum[r[i]]-s[i]+yr[l[i]]),0);
end;
procedure pdown(i:longint);
begin
    if rev[i] then
    begin
		if l[i]>0 then prev(l[i]);
		if r[i]>0 then prev(r[i]);
		rev[i]:=false;
    end;

     if en[i] then
     begin
		pen(l[i],entime[i]);
        pen(r[i],entime[i]);
		en[i]:=false;
		entime[i]:=0;
     end;

    if sa[i]<>0 then
	begin
		if l[i]>0 then psa(l[i],sa[i],satime[i]);
		if r[i]>0 then psa(r[i],sa[i],satime[i]);
		sa[i]:=0;
		satime[i]:=0;
	end;
end;
procedure left(i:longint);
var x,y:longint;
begin
	x:=r[i];
	y:=l[x];
	r[i]:=y;
	if y>0 then fa[y]:=i;
	if fa[i]>0 then
		if l[fa[i]]=i then l[fa[i]]:=x else r[fa[i]]:=x;
	fa[x]:=fa[i];
	l[x]:=i;
	fa[i]:=x;
	pup(i);
	if i=root then root:=x;
end;

procedure right(i:longint);
var x,y:longint;
begin
	x:=l[i];
	y:=r[x];
	l[i]:=y;
	if y>0 then fa[y]:=i;
	if fa[i]>0 then
		if l[fa[i]]=i then l[fa[i]]:=x else r[fa[i]]:=x;
	fa[x]:=fa[i];
	r[x]:=i;
	fa[i]:=x;
	pup(i);
	if i=root then root:=x;
end;

procedure splay(x,f:longint);
var y,z:longint;
begin
	pdown(x);
	while fa[x]<>f do
	begin
		y:=fa[x];
		z:=fa[y];
                if z>0 then pdown(z);
                if y>0 then pdown(y);
		if z=f then
			if l[y]=x then right(y) else left(y)
			else
			if l[z]=y then
				if l[y]=x then begin right(z);right(y);end
						  else begin left(y);right(z);end
					  else
				if l[y]=x then begin right(y);left(z);end
						  else begin left(z);left(y);end;
        end;
        pup(x);
end;

procedure sel(x,f:longint);
var t:longint;
begin
	t:=root;
	repeat
		pdown(t);
		if x=size[l[t]]+1 then break
		else
		if x<size[l[t]]+1 then t:=l[t]
		else begin dec(x,size[l[t]]+1);t:=r[t];end;
	until false;
	splay(t,f);
end;

function tiqu(x,y:longint):longint;
begin
	if x=1 then
		if y=n then exit(root)
			   else begin sel(y+1,0);exit(l[root]);end
		   else
	if y=n then begin sel(x-1,0);exit(r[root]);end
		   else begin sel(x-1,0);sel(y+1,root);exit(l[r[root]]);end;
end;

procedure build(x,y,f,t:longint);
begin
	if f=0 then root:=(x+y) div 2
	else
	if t=0 then l[f]:=(x+y) div 2 else r[f]:=(x+y) div 2;
	fa[(x+y) div 2]:=f;
	if x<=(x+y) div 2-1 then build(x,(x+y) div 2-1,(x+y) div 2,0);
	if (x+y) div 2+1<=y then build((x+y) div 2+1,y,(x+y) div 2,1);
	pup((x+y) div 2);
end;

procedure print(i:longint);
begin
        pdown(i);
        if l[i]>0 then print(l[i]);
        if s[i]=1 then write('(') else write(')');
        if r[i]>0 then print(r[i]);
        pup(i);
end;
function check:boolean;
var i:longint;
begin
        for i:=1 to n do
        if (xl[i]<0)or(xr[i]<0)or(yl[i]<0)or(yr[i]<0) then exit(false);
        exit(true);
end;

begin
		assign(input,'Brackets.in');
		assign(output,'Brackets.out');
		reset(input);rewrite(output);

		readln(n,m);
		for i:=1 to n do
		begin
			read(c);
			if c='(' then s[i]:=1 else s[i]:=-1;
		end;
		readln;

		build(1,n,0,0);

		for i:=1 to m do
		begin
			str:=reads;
			x:=readn;
			y:=readn;
			p:=tiqu(x,y);
			if str='Query' then
			begin
				writeln((yl[p]+1) div 2+(xr[p]+1) div 2);
			end
			else
			if str='Replace' then
			begin
				read(c);
				if c='(' then psa(p,1,i) else psa(p,-1,i);
				while fa[p]>0 do begin pup(fa[p]);p:=fa[p];end;
			end
			else
			if str='Swap' then
			begin
				prev(p);
				while fa[p]>0 do begin pup(fa[p]);p:=fa[p];end;
			end
			else
			if str='Invert' then
			begin
                pen(p,i);
				while fa[p]>0 do begin pup(fa[p]);p:=fa[p];end;
			end;
			readln;

            //print(root);
            //writeln;
            //if not check then writeln('no');
		end;
        close(input);close(output);
end.