Faster R-CNN边框回归方法的几点思考

最近重新看了Faster R-CNN系列论文，对其中边框回归的目标和损失函数的设计思路有了新的认识，这里记录一下。

对于边框回归问题，假设我们已经得到了预测框\((P_{x},P_{y},P_{w},P_{h})\),即一个预测框中心点坐标和它的长宽，在Faster R-CNN中，有两个东西可以看成是预测框，第一个是RPN中的Anchor，第二个是RPN预测得到的候选框。有了预测框，如何得到真实的目标框\((G_{x},G_{y},G_{w},G_{h})\)呢？一种直观的思路就是寻找一个映射关系，使得预测框映射的结果\(\hat{G}\)尽可能接近真实框。论文作者采用了平移加缩放的思路。

首先对中心点进行平移：

\(\hat{G}_{x}=P_{w}t_{x}+P_{x}\)

\(\hat{G}_{y}=P_{h}t_{y}+P_{y}\)

再做尺度变换：

\(\hat{G}_{w}=P_{w}e^{t_{w}}\)

\(\hat{G}_{h}=P_{h}e^{t_{h}}\)

这里，加上指数e的原因是需要保证缩放系数大于0

因此回归就是学习上述的四个t值，即

\(t_{x}=(G_{x}-P_{x})/P_{w}\)

\(t_{y}=(G_{y}-P_{y})/P_{h}\)

\(t_{w}=log(G_{w}-P_{w})\)

\(t_{h}=log(G_{h}-P_{h})\)

• 疑问一：

  为什么这里要用\(P_{w}t_{x}\)的形式而不是直接用一个变量\(O_{x}\)表示平移量（等价于为什么需要除以\(P_{w}\)），主要原因就在于需要保持尺度不变性。如下图所示，假如图片中有两个大小不一样的人，网络需要能将他们都判断为人，则其对应特征\(\phi_{1}=\phi_{2}\),如果我们直接学习坐标差值，以x坐标为例，学习到的映射分别为\(t_{x1}=f(\phi_{1})=x_{1}-p_{1}\)和\(t_{x2}=f(\phi_{2})=x_{2}-p_{2}\)，很明显两者的值不相等，也就是同一个x对应不同的y，这显然不满足函数定义。

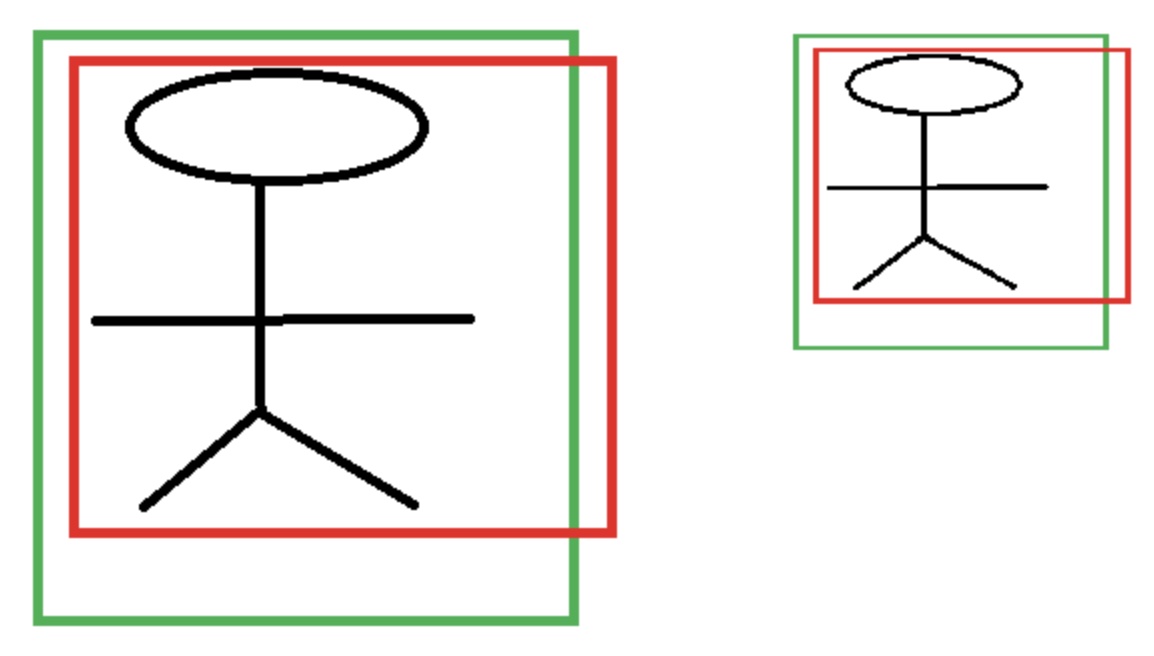
• 疑问二：

  为什么对w、h回归需要加上log？因为需要保证缩放系数大于0加了指数e，那么反过来推导就需要变为log。

参考：

https://blog.csdn.net/zijin0802034/article/details/77685438

https://www.cnblogs.com/dudumiaomiao/p/6560841.html

https://blog.csdn.net/u013803065/article/details/88607226

https://www.cnblogs.com/hotsnow/p/9951046.html

https://zhuanlan.zhihu.com/p/70557171