后缀数组学习笔记

\(\texttt{Introduction}\)

\(\texttt{DP}\) 题刷不动，补以前的题发现题题不会，所以来学习新算法充实大脑。

\(\texttt{SA}\) 码量小，应用广，思路妙，是难得一见的好字符串算法！

\(\texttt{Description}\)

给你一个长度为 \(n\) 的字符串，要你对他的所有后缀进行排序，输出每一个后缀的排名。

\(\texttt{Solution}\)

后缀数组的经典实现方法为倍增法，主要利用的原理是将一个字符串拆成两个关键字再进行比较，为了后文方便描述，我们先将各个数组的含义做一个定义。

• \(\texttt{sa}(i)\) 表示排名为 \(i\) 的后缀的起始位置

• \(\texttt{rk}(i)\) 表示起始位置为 \(i\) 的后缀的排名

对于这两个数组，显然存在 \(\texttt{sa}(\texttt{rk}(i))=\texttt{rk}(\texttt{sa}(i))=i\)，这就是下面做法中这两个数组互相转化的原理。

我们首先将问题特殊化，考虑每个后缀如果都只有一个字符的话，那么我们可以直接对他排序，得到排名。

这时候如果存在两个字符，我们可以将这两个字符视作两个关键字，那么这时候就是双关键字了 \((\texttt{rk}(i),\texttt{rk}(i+1))\)。

这样子的话会存在一个问题，我们是无法对直接对 \(\texttt{rk}\) 数组进行排序的，这时候 \(\texttt{sa}\) 数组的作用就体现出来了：

\(\texttt{sa}(x)\) 与 \(\texttt{sa}(y)\) 需要交换，就是当 \((\texttt{rk}(\texttt{sa(x)}),\texttt{rk}(\texttt{sa(x)+1})>(\texttt{rk}(\texttt{sa(y)}),\texttt{rk}(\texttt{sa(y)+1}))\)。

那么这个时候就可以排序了，然后 \(\texttt{rk}\) 也可以通过与 \(\texttt{sa}\) 的关系求出。

然后我们考虑如果存在长度为 \(2^k\)，那么也可以通过类似的方法从 \(2^{k-1}\) 的 \(\texttt{rk}\) 数组中得到，这个时候我们的复杂度是 \(\mathcal O(n\log^2 n)\)，不够优秀。

目前的代码是这样的：

 scanf("%s",S+1);n=strlen(S+1);
 for (i=1;i<=n;i++) sa[i]=i;
 for (i=1;i<=n;i++) rk[i]=S[i]-'a'+1;len=0;
 	sort(sa+1,sa+n+1,cmp);
 	for (i=1;i<=n;i++) lst[i]=rk[i];tot=0;
 	for (i=1;i<=n;i++)
 	    if ((lst[sa[i]]==lst[sa[i-1]])&&(lst[sa[i]+len]==lst[sa[i-1]+len])) rk[sa[i]]=tot;
 	    else rk[sa[i]]=++tot;
 for (len=1;len<=n;len<<=1){
    sort(sa+1,sa+n+1,cmp);
 	for (i=1;i<=n;i++) lst[i]=rk[i];tot=0;
 	for (i=1;i<=n;i++)
 	    if ((lst[sa[i]]==lst[sa[i-1]])&&(lst[sa[i]+len]==lst[sa[i-1]+len])) rk[sa[i]]=tot;
 	    else rk[sa[i]]=++tot;
 }
  for (i=1;i<=n;i++) printf("%d ",sa[i]);puts("");

如何优化到 \(\mathcal O(n\log n)\)？

我们注意到这道题的值域不是很大（与 \(n\) 几乎相等）,这时候应该想到计数排序，但是有一个问题就是计数排序是单关键字的，而这里是双关键字的，那么是否可以将计数排序进行拓展？

必然是可以的，这种排序叫做基数排序，复杂度是 \(\mathcal O(kn+\sum_{i=1}^{k} w_i)\)，其中 \(k\) 是关键字的个数，我们会发现在后缀数组需要的排序下，这种排序是要快于快排的。

那么基数排序又应该如何实现呢？

我们首先将数列按照第二关键字排序，然后按第一关键字排序的时候，如果相同保持原来的顺序不动，这就是双关键字时的实现方式，然后每一个关键字排序都用一个计数排序维护就可以了。

那么这个时候的代码是这样的：

void sort(int l,int r){
	tot=0;
	for (i=n;i>n-len;i--) B[++tot]=i;
	for (i=1;i<=n;i++)
	    if (sa[i]>len) B[++tot]=sa[i]-len;
	for (i=1;i<=max(n,250);i++) fre[i]=0;
	for (i=1;i<=n;i++) fre[rk[B[i]]]++;
	for (i=1;i<=max(n,250);i++) fre[i]=fre[i-1]+fre[i];
	for (i=n;i>=1;i--) sa[fre[rk[B[i]]]--]=B[i];
}
int main()
{
 scanf("%s",S+1);n=strlen(S+1);
 for (i=1;i<=n;i++) sa[i]=i;
 for (i=1;i<=n;i++) rk[i]=S[i];len=0;
 sort(1,n);
 for (i=1;i<=n;i++) lst[i]=rk[i];tot=0;
 for (i=1;i<=n;i++)
   if ((lst[sa[i]]==lst[sa[i-1]])&&(lst[sa[i]+len]==lst[sa[i-1]+len])) rk[sa[i]]=tot;
   else rk[sa[i]]=++tot;
 for (len=1;len<=n;len<<=1){
    sort(1,n);
 	for (i=1;i<=n;i++) lst[i]=rk[i];tot=0;
 	for (i=1;i<=n;i++)
 	    if ((lst[sa[i]]==lst[sa[i-1]])&&(lst[sa[i]+len]==lst[sa[i-1]+len])) rk[sa[i]]=tot;
 	    else rk[sa[i]]=++tot;
 }
  for (i=1;i<=n;i++) printf("%d ",sa[i]);puts("");
 return 0;
}

\(\texttt{Extra}\)

后缀数组还有一个东西叫做 \(\texttt{Height}\) 数组，这个东西又是干什么的呢？

还是先上定义：

• \(\texttt{LCP}(i,j)\) 表示后缀 \(i\) 和后缀 \(j\) 的最长公共前缀

• \(\texttt{Height}(i)=\texttt{LCP}(\texttt{sa}(i),\texttt{sa}(i-1))\)

我们有一个结论：\(\texttt{Height}(\texttt{rk}(i))\ge\texttt{Height}(\texttt{rk}(i-1))-1\)

$\texttt{Proof}$

咕咕咕

然后暴力做就好了呀。

神奇的习题

P4070 [SDOI2016]生成魔咒

动态加字符，询问本质不同子串个数

如果单次询问，就是求 \(\texttt{Height}\) 数组的和，而这里是往后面动态加点，这样子会导致每一个后缀的排名都有可能移动不止一位，显然是不优的，那么我们考虑将字符串倒置，那么这样子每次操作就是往最前面加点。

我们考虑快速算出这个新后缀的排名，好像可以用 \(\texttt{set}\) 解决，就是考虑把首位和除首位外的后缀的排名弄成一个二元组，然后 \(\texttt{set}\) 就可以找到他第一个符合条件的位置，但是我们知道了新的排名，怎么更新 \(\texttt{Height}\) 数组呢？

\(\color{black}{\texttt{E}}\color{red}{\texttt{ricQian}}\) 曾经说过，正着不好做，我们就倒着做，但是这道题显然不能倒着做，删点肯定更加麻烦，但是我们可以把所有点先全部加进去，求出 \(\texttt{sa}\)，那么在之后的运算中，其实 \(\texttt{sa}\) 的值虽然会改变，他是他们的相对大小是一定不会改变的，然后好像就可以做了？

\(\color{black}{\texttt{E}}\color{red}{\texttt{ricQian}}\) 又告诉了我，不要局限于 \(\texttt{Height}\) 数组的改变，我们考虑加进这个数会产生什么样的贡献，采用正难则反的策略，我们求出他的前驱和后继，那么这个点和这两个点的 \(\texttt{LCP}\) 的 \(\max\) 就是重复出现过的，那么总数减去这个多余的就好了。

for (now=1;now<=n;now++){
    G.insert(rk[n-now+1]);
    it=G.find(rk[n-now+1]);up=-1;
    if (it!=G.begin()){
         it--;
         int lft=*it;
         up=max(up,find(lft+1,rk[n-now+1]));
    }it=G.find(rk[n-now+1]);it++;
    if (it!=G.end()){
    	int rit=*it;
    	up=max(up,find(rk[n-now+1]+1,rit));
	}
	if (up==-1) ans=1;
	else ans+=now-up;
	printf("%lld\n",ans);
}

P1117 [NOI2016] 优秀的拆分

给定一个字符串 \(\texttt{S}\),问每个子串拆分成 \(\texttt{A+A+B+B}\) 形式的方案的总和

一道题耗了我 \(\texttt{6}\) 个小时，最后还是只能看题解，我只能说为什么这道题是紫题？

我们假设这次做的长度为 \(\texttt{len}\)，考虑到 \(\texttt{len}\) 的位置恰好是第一的长度为 \(\texttt{len}\) 的子串的结尾，那么我们考虑从这个点开始每 \(\texttt{len}\) 个设一个关键点。

而这个时候就是本题最难的部分了，证明不难，但是想到这个结论十分的困难啊！

我们考虑计算相邻两个关键点的 \(\texttt{LCP}\) 和 \(\texttt{LCS}\)，下面一张图，会解释所有：

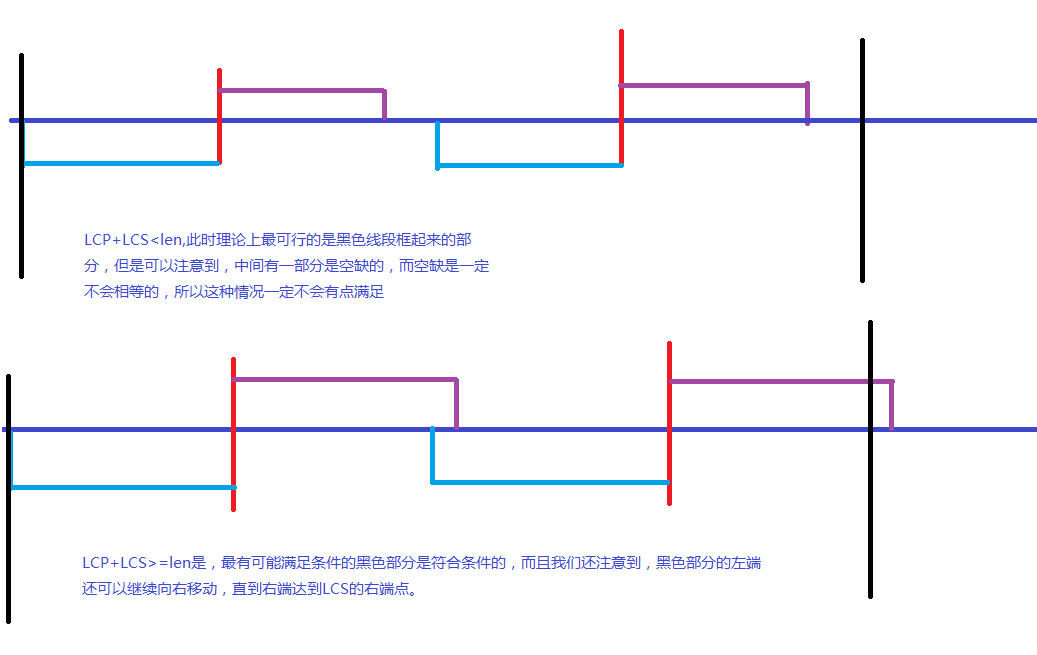
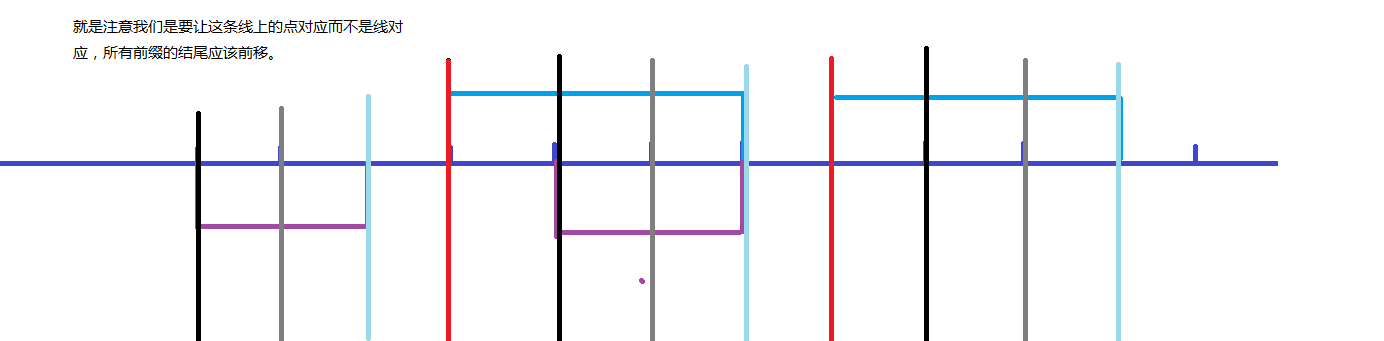
但是不是只要理解了这张图就好了，实现过程中还是有无数的细节，\(\texttt{LCP}\) 自然是简单的，但是这个 \(\texttt{LCS}\) 就会产生一个细节，还是看图：

但是给了 \(\texttt{95}\) 分暴力分是好的

总共用了 \(\texttt{10}\) 个小时以上在这道【】【】题上

$\texttt{Code}$

#include<bits/stdc++.h>
using namespace std;
inline long long read()
{
  long long x=0,f=1;char ch=getchar();
  while(!isdigit(ch)&&ch!='-')ch=getchar();
  if(ch=='-')f=-1,ch=getchar();
  while(isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
  return x*f;
}
int st1[1001010][22],st2[1001010][22];
char S[1001010];
long long G1,G2,G,st,ed,tot,rk1[1001010],rk2[1001010],k,lg[1001010],lft,rit,tn,ans,mn,j,lst[1001010],n,i,pre[1001010],suf[1001010],B[1001010],fre[1001010],sa[1001010],rk[1001010],len,K,H[1001010],a[1001010];
void sort(int l,int r){tot=0;
	for (int i=n;i>n-len;i--) B[++tot]=i;
	for (i=1;i<=n;i++)
	    if (sa[i]>len) B[++tot]=sa[i]-len;
	for (i=1;i<=n;i++) fre[rk[B[i]]]++;
	for (i=1;i<=max(n,(long long)444);i++) fre[i]=fre[i-1]+fre[i];
	for (i=n;i>=1;i--) sa[fre[rk[B[i]]]--]=B[i];
	for (i=0;i<=max(n,(long long)444);i++) fre[i]=0;
}void Remake(){
	for (i=1;i<=n;i++) lst[i]=rk[i];tot=0;
	for (i=1;i<=n;i++)
	    if ((lst[sa[i]]==lst[sa[i-1]])&&((lst[sa[i]+len]==lst[sa[i-1]+len]))) rk[sa[i]]=tot;
	    else rk[sa[i]]=++tot;
}
int find1(int l,int r){int len=lg[r-l+1];return min(st1[l][len],st1[r-(1<<len)+1][len]);}
int find2(int l,int r){int len=lg[r-l+1];return min(st2[l][len],st2[r-(1<<len)+1][len]);}
void solve(int opt){n=tn;
    memset(lst,0,sizeof(lst));//memset(rk,0,sizeof(rk));memset(sa,0,sizeof(sa));
	for (i=1;i<=n;i++) sa[i]=i,rk[i]=S[i];
	len=0;
	sort(1,n);Remake();
    for (len=1;len<=n;len<<=1) sort(1,n),Remake();
	K=0;S[n+1]='&';
    for (i=1;i<=n;i++){
      	if (rk[i]==0) continue;if (K) K--;
	    while ((S[sa[rk[i]]+K]==S[sa[rk[i]-1]+K])&&(K<=n)) K++;H[rk[i]]=K;
        }
    if (opt==1){
    	for (i=1;i<=n;i++) st1[i][0]=H[i],rk1[i]=rk[i];
    	for (j=1;j<=lg[n];j++)
    	    for (i=1;i<=n-(1<<j)+1;i++)
    	         st1[i][j]=min(st1[i][j-1],st1[i+(1<<(j-1))][j-1]);
    	return ;
	}
	for (i=1;i<=n;i++) st2[i][0]=H[i],rk2[i]=rk[i];
	for (j=1;j<=lg[n];j++)
	    for (i=1;i<=n-(1<<j)+1;i++)
	         st2[i][j]=min(st2[i][j-1],st2[i+(1<<(j-1))][j-1]);
}
void Main(){
	scanf("%s",S+1);n=strlen(S+1);tn=n;
	for (i=2;i<=n;i++) lg[i]=lg[i>>1]+1;
	solve(1);
	for (i=1;i<=n/2;i++) swap(S[i],S[n-i+1]);solve(-1);
	for (len=1;len<=n;len++)
	    for (st=len;st+len<=n;st+=len){
	   	    ed=st+len;lft=rk1[st];rit=rk1[ed];if (lft>rit) swap(lft,rit);G1=find1(lft+1,rit);
	   	    lft=rk2[n-st+2];rit=rk2[n-ed+2];if (lft>rit) swap(lft,rit);G2=find2(lft+1,rit);
	   	    G1=min(G1,len);G2=min(G2,len-1);
	   	    if (G1+G2>=len){
	   	    	G=G1+G2-len+1;
				   suf[st-G2]++;suf[st-G2+G]--;pre[ed+G1-G]++;pre[ed+G1]--;
			   }
	   }
	for (i=1;i<=n;i++) pre[i]=pre[i-1]+pre[i],suf[i]=suf[i-1]+suf[i];
	ans=0;  
	for (i=2;i<n;i++) ans=ans+pre[i]*suf[i+1];
	for (i=0;i<=n+1;i++) pre[i]=suf[i]=0;
	printf("%lld\n",ans);
	return; 
}
int main()
{
	for (int Testing=read();Testing;Testing--) Main();
return 0;
}