线段树——区间覆盖理解

本人正在写树剖，结果线段树不会维护了，还是太菜了，然后就卡了半天。。。

这里以我卡的那题为解释

题目在此

这道题思路我自认为还是很板的，

• 操作1：安装的话就是输出本点深度减去它到根有几个1，再把这个点到根的链都变为1

• 操作2：删除就是先输出子树有多少个1，再全删了

我一直在想把每个节点都标为 \(1\) 和 \(0\) ，但被一堆树搞晕了，不知道怎么用线段树去维护权值，一直在想节点怎么维护子树

信息，忘了线段树具体是怎么运作的了，只能说太唐了我。

实际上这就是一个线段树区间覆盖，而线段树是根据节点的 \(dfs\) 序维护的，也就是最下面一层的节点就是每一个原树上的点

所以 \(1\) 的个数就是节点维护区间的长度，而这每一个节点维护的信息对应的实际上就是原树上的一段链，他们维护的区间与

原树是一一对应的，所以在求区间和时，就是把区间分成几部分，去找每一部分对应的区间求和即可

各位要是有些迷糊的话可以用下面两个图对应一下

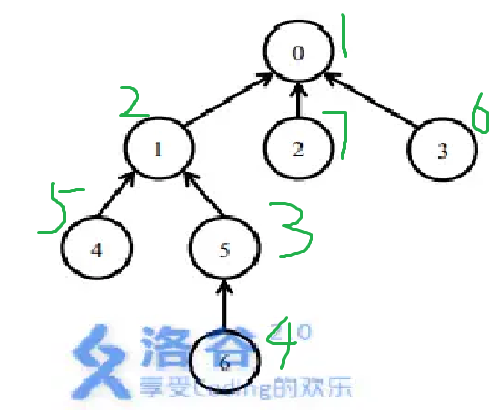
这个图对应的线段树应该是

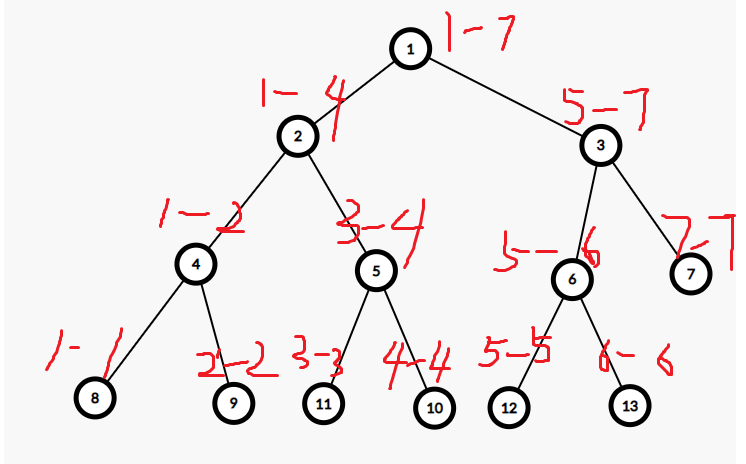
（字有点丑，不要在意那些细节）

假设我们先安装 \(4\) 那么线段树上 \(8,9,12\) 节点变为 \(1\) 然后向上更新，那么我们再安装一个 \(6\) 时查询区间为

\(1-4\) 但由于更新, \(2\) 节点的值就变为 \(2\) ,所以查询结果就是 \(2\) 了，这是因为线段树上来维护树剖，会把一条

链分成几部分来求，求的是不同重链的和，也就是上述的样例，它会先求 \(5-5\) ，再求 \(1-2\) ，而不是直接求 \(1-5\)

这也是线段树不能直接求链的原因，而第二个样例是因为，\(0-1-5-6\)，这条链本身就是一条重链，它之前被其他链的值

影响过（证明肯定之前有节点跳到并可以跳到这条链上），这两条链到根一定是有重叠的部分的（不然影响不到），所以

也就是说有其他节点安装是把这条重链上的部分点影响了，所以查到值直接返回就是答案

solution

#include<bits/stdc++.h>
#define lid id<<1
#define rid id<<1|1 
const int maxn=1e6+10;
const int inf=0x7f7f7f7f;
using namespace std;
int n,t,a[maxn<<2];
struct tree{int l,r,lazy,sum;}m[maxn<<4]; 
int tot,head[maxn<<1],to[maxn<<2],nxt[maxn<<2];
int size[maxn],wson[maxn],fa[maxn],dep[maxn],top[maxn];
int dfn[maxn],pre[maxn],cnt=0;
int mod,root;
void add(int x,int y)
{
	to[++tot]=y;nxt[tot]=head[x];head[x]=tot;
}
void addm(int x,int y)
{
	add(x,y),add(y,x);
}
void dfs1(int u,int f)
{
	size[u]=1;
	for(int i=head[u];i;i=nxt[i])
	{
		int y=to[i];
		if(y==f)continue;
		dep[y]=dep[u]+1;
		fa[y]=u;
		dfs1(y,u);
		size[u]+=size[y];
		if(size[y]>size[wson[u]])wson[u]=y;
	}
}
void dfs2(int u,int topfa)
{
	dfn[u]=++cnt;
	pre[cnt]=u;
	top[u]=topfa;
	if(wson[u])dfs2(wson[u],topfa);
	for(int i=head[u];i;i=nxt[i])
	{
		int y=to[i];
		if(y==fa[u]||y==wson[u])continue;
		dfs2(y,y);	
	}
}
inline void up(int id)
{
	m[id].sum=m[lid].sum+m[rid].sum;
}
inline void down(int id,int l,int r,int mid)
{
	if(m[id].lazy<0)return ;	
	m[lid].lazy=m[rid].lazy=m[id].lazy;
	if(m[id].lazy==0) m[lid].sum=m[rid].sum=0;
	else m[lid].sum=mid-l+1,m[rid].sum=r-mid;
	m[id].lazy=-1;
}
void build(int id,int l,int r)
{
	m[id].l=l;
	m[id].r=r;
	if(l==r){m[id].lazy=-1;return;};	
	int mid=(l+r)>>1;
	build(lid,l,mid);
	build(rid,mid+1,r);
} 
int querysum(int id,int s,int tt,int y)
{
	int l=m[id].l,r=m[id].r,ans=0;
//	cout<<id<<" "<<l<<" "<<r<<" "<<m[id].sum<<endl; 
	if(s<=l&&r<=tt)
	{
		ans=m[id].sum;
		m[id].lazy=y;
		m[id].sum=(r-l+1)*y;
		return ans;
	}
	int mid=(l+r)>>1;
	down(id,l,r,mid);
	if(s<=mid)ans+=querysum(lid,s,tt,y);
	if(tt>mid)ans+=querysum(rid,s,tt,y);
	up(id);
//	cout<<"up: "<<id<<" "<<l<<" "<<r<<" "<<m[id].sum<<endl;
	return ans;
} 
int qsum(int x,int y)
{
	int ans=0;
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		ans+=querysum(1,dfn[top[x]],dfn[x],1);
		x=fa[top[x]];
	}
	if(dep[x]<dep[y])swap(x,y);
	ans+=querysum(1,dfn[y],dfn[x],1);
	return ans;
}
int main()
{
	scanf("%d",&n);
	for(int i=2;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		x++;
		addm(i,x);
	}
	dfs1(1,0);
	dfs2(1,1);
	build(1,1,n);
	scanf("%d",&t);
	char ss[10];
	int x,y,z;
//	for(int i=1;i<=n;i++)
//		cout<<dfn[i]<<" "; 
	while(t--)
	{
		cin>>ss+1;
		if(ss[1]=='i')
		{
			scanf("%d",&x);
			x++;
			int ans=qsum(1,x);
//			cout<<ans<<endl;
			printf("%d\n",dep[x]+1-ans);
		}
		else
		{
			scanf("%d",&x);
			x++;
			printf("%d\n",querysum(1,dfn[x],dfn[x]+size[x]-1,0));
		}
	}
	return 0;
}