分类回归树（Classification and Regression Tree，CART）

在构建回归树时，主要有两种不同的树：
  • 回归树(Regression Tree)，其每个叶节点是单个值
  • 模型树(Model Tree)，其每个叶节点是一个线性方程
  • 分类树(Classification Tree)
　　在进行树的左右子树划分时，有一个很重要的量，即给定的值，特征值大于这个给定的值的属于一个子树，小于这个给定的值的属于另一个子树。
　　这个给定的值的选取的原则是使得划分后的子树中的“混乱程度”降低。如何定义这个混乱程度是设计CART算法的一个关键的地方。
　　在ID3算法中我们使用的信息熵和信息增益的概念。信息熵就代表了数据集的紊乱程度。
　　对于连续型的问题，我们可以使用方差的概念来表达混乱程度，方差越大，越紊乱。所以我们要找到使得切分之后的方差最小的划分方式。
 
 对于ID3 & C4.5 & CART：
　　用信息增益率来选择属性。ID3选择属性用的是子树的信息增益，这里可以用很多方法来定义信息，ID3使用的是熵（entropy， 熵是一种不纯度度量准则），也就是熵的变化值，
　　C4.5用的是信息增益率。CART分类树和C4.5都是由ID3衍生而来。CART最优属性是用GINI系数来选择的。注意CART是二分树，也就是二叉树。
 
CART算法的重要基础包含以下三个方面： 
　　（1）二分(Binary Split)：在每次判断过程中，都是对观察变量进行二分。 
　　CART算法采用一种二分递归分割的技术，算法总是将当前样本集分割为两个子样本集，使得生成的决策树的每个非叶结点都只有两个分枝。因此CART算法生成的决策树是结构简洁的二叉树。因此CART算法适用于样本特征的取值为是或非的场景，对于连续特征的处理则与C4.5算法相似。 
　　（2）单变量分割(Split Based on One Variable)：每次最优划分都是针对单个变量。 
　　（3）剪枝策略：CART算法的关键点，也是整个Tree-Based算法的关键步骤。 
　　剪枝过程特别重要，所以在最优决策树生成过程中占有重要地位。有研究表明，剪枝过程的重要性要比树生成过程更为重要，对于不同的划分标准生成的最大树(Maximum Tree)，在剪枝之后都能够保留最重要的属性划分，差别不大。反而是剪枝方法对于最优树的生成更为关键。
CART回归树和模型树 
当数据拥有众多特征并且特征之间关系十分复杂时，构建全局模型的想法就显得太难了，也略显笨拙。而且，实际生活中很多问题都是非线性的，不可能使用全局线性模型来拟合任何数据。一种可行的方法是将数据集切分成很多份易建模的数据，然后利用线性回归技术来建模。如果首次切分后仍然难以拟合线性模型就继续切分。在这种切分方式下，树结构和回归法就相当有用。 
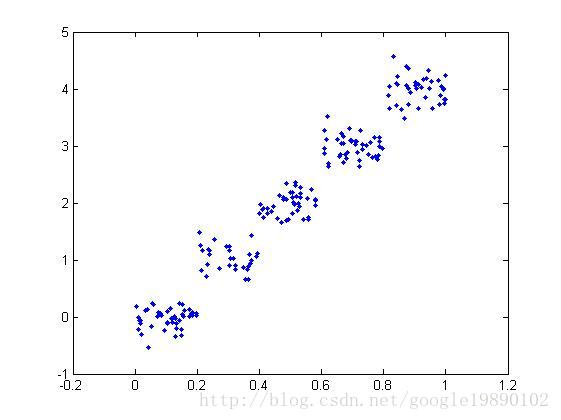
回归树与分类树的思路类似，但叶节点的数据类型不是离散型，而是连续型，对CART稍作修改就可以处理回归问题。CART算法用于回归时根据叶子是具体指还是另外的机器学习模型又可以分为回归树和模型树。但无论是回归树还是模型树，其适用场景都是：标签值是连续分布的，但又是可以划分群落的，群落之间是有比较鲜明的区别的，即每个群落内部是相似的连续分布，群落之间分布确是不同的。所以回归树和模型树既算回归，也称得上分类。 
回归是为了处理预测值是连续分布的情景，其返回值应该是一个具体预测值。回归树的叶子是一个个具体的值，从预测值连续这个意义上严格来说，回归树不能称之为“回归算法”。因为回归树返回的是“一团”数据的均值，而不是具体的、连续的预测值（即训练数据的标签值虽然是连续的，但回归树的预测值却只能是离散的）。所以回归树其实也可以算为“分类”算法，其适用场景要具备“物以类聚”的特点，即特征值的组合会使标签属于某一个“群落”，群落之间会有相对鲜明的“鸿沟”。如人的风格是一个连续分布，但是却又能“群分”成文艺、普通和2B三个群落，利用回归树可以判断一个人是文艺还是2B，但却不能度量其有多文艺或者多2B。所以，利用回归树可以将复杂的训练数据划分成一个个相对简单的群落，群落上可以再利用别的机器学习模型再学习。 
模型树的叶子是一个个机器学习模型，如线性回归模型，所以更称的上是“回归”算法。利用模型树就可以度量一个人的文艺值了。 

 

GBDT 梯度boosting决策树 注意它和 AdaBoosting区别还是挺大的。ada是每次迭代都会将样本的权重修改一下，之前预测错误的权重up  预测正确的down。而GBDT，每次迭代所产生的树都是根据之前的残差来构建的。可以理解为残差是它每次迭代的预测值y
 Gradient Boost与传统的Boost的区别是，每一次的计算是为了减少上一次的残差(residual)，而为了消除残差，我们可以在残差减少的梯度(Gradient)方向上建立一个新的模型。所以说，在Gradient Boost中，每个新的模型的简历是为了使得之前模型的残差往梯度方向减少，与传统Boost对正确、错误的样本进行加权有着很大的区别。