损失函数总结

　　损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是指经验风险损失函数加上正则项。通常表示为如下：（整个式子表示的意思是找到使目标函数最小时的θ值。）

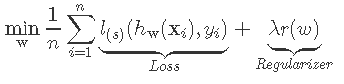
$$\lambda = \frac{1}{C}$$

一、分类损失函数

1.二分类损失函数

$y \in \{-1,+1\}$

Loss$l(h_w(X_i,yi))$	代表算法	说明
1.Hing-Loss $$max\left[1-h_{\mathbf{w}}(\mathbf{x}_{i})y_{i},0\right]^{p}$$	标准SVM(p=1) (Differentiable) Squared Hingeless SVM (p=2)	当用于标准SVM时，损失函数表示线性分隔符与其中任一类中的最近点之间的边距长度。 只有在p = 2时处处可导。
2.Log-Loss $$log(1+e^{-h_{\mathbf{w}}(\mathbf{x}_{i})y_{i}})$$	Logistic回归	机器学习中最受欢迎的损失功能之一，因为它能输出概率
3.Exponential Loss  $$e^{-h_{\mathbf{w}}(\mathbf{x}_{i})y_i}$$	Adaboost	错误预测的丢失随着值的增加呈指数增长$$-h_w(x_i)y_i$$
4.Zero-One Loss  $$\delta(\textrm{sign}(h_{\mathbf{w}}(\mathbf{x}_{i}))\neq y_{i})$$	实际分类损失	不连续，不容易优化

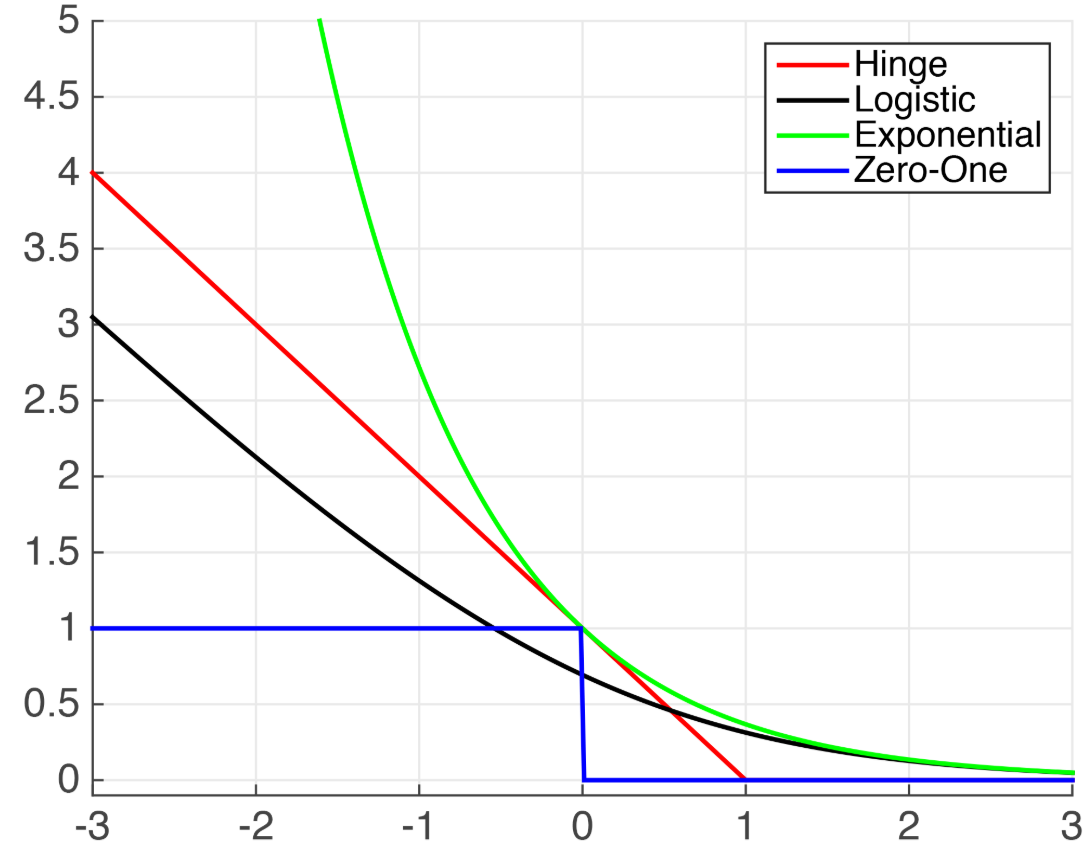
横坐标：$h(X_i)y_i$ |  纵坐标：损失值

 

关于损失函数的补充说明：

• 当$z\rightarrow-\infty$，log-loss和hinge loss会逐渐平行
• 指数损失和hinge损失大于Zero-one 损失的上界
• Zero-one 损失当预测正确的时候为0，预测错误时为1

1.1 hinge loss

1.2 log loss

（1）log loss的一阶二阶导数

损失函数：$y\ln\left(p\right)+\left(1-y\right)\ln\left(1-p\right)$

$p = \dfrac{1}{(1 + e^{-x})}$

$\frac{\partial f}{\partial p}=\frac{p-y}{\left(1-p\right)p}$

$\frac{\partial p}{\partial x}=p(1-p)$

$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial p}\frac{\partial p}{\partial x}=p-y$

$\frac{\partial^2 f}{\partial x^2}=\frac{\partial}{\partial x}(\frac{\partial f}{\partial x})=\frac{\partial}{\partial x}(p-y)=\frac{\partial p}{\partial x}=p(1-p)$

（2）logloss与交叉熵的等价性

 

 

1.3 exponential loss

1.4 zero-one loss

 

 

二、回归损失函数

Loss $\ell(h_{\mathbf{w}}(\mathbf{x}_i,y_i))$	说明
1.Squared Loss $$(h(\mathbf{x}_{i})-y_{i})^{2}$$	也被称为均分误差| 二次损失 | L2损失 | 普通最小二乘法(OLS) | Mean Square Error, Quadratic Loss, L2 Loss 优点：处处可导 缺点：对异常值敏感
2.Absolut Loss $$|h(\mathbf{x}_{i})-y_{i}|$$	优点：对噪音不敏感 缺点：0点不可导
3.Huber Loss $\frac{1}{2}\left(h(\mathbf{x}_{i})-y_{i}\right)^{2}$  if $|h(\mathbf{x}_{i})-y_{i}|<\delta$ otherwise $$\delta(|h(\mathbf{x}_{i})-y_{i}|-\frac{\delta}{2})$$	平滑绝对损失 优点：结合了平方损失和绝对损失；一阶可导 当损失很小时采用平方损失，当损失很大时采用绝对损失
4.fair loss $$c^2(\frac{|x|}{c}-ln(\frac{|x|}{c}+1))$$
5.Log-Cosh Loss $$log(cosh(h(\mathbf{x}_{i})-y_{i}))$$ $$cosh(x)=\frac{e^{x}+e^{-x}}{2}$$	优点：与Huber损失类似，但处处二阶可导 缺点：对于误差很大的预测，其梯度和hessian是恒定的
6.Quantile Loss（分位数损失）	优点：基于Quantile Loss的回归模型可以提供合理的预测区间，即使是对于具有非常数方差或非正态分布的残差

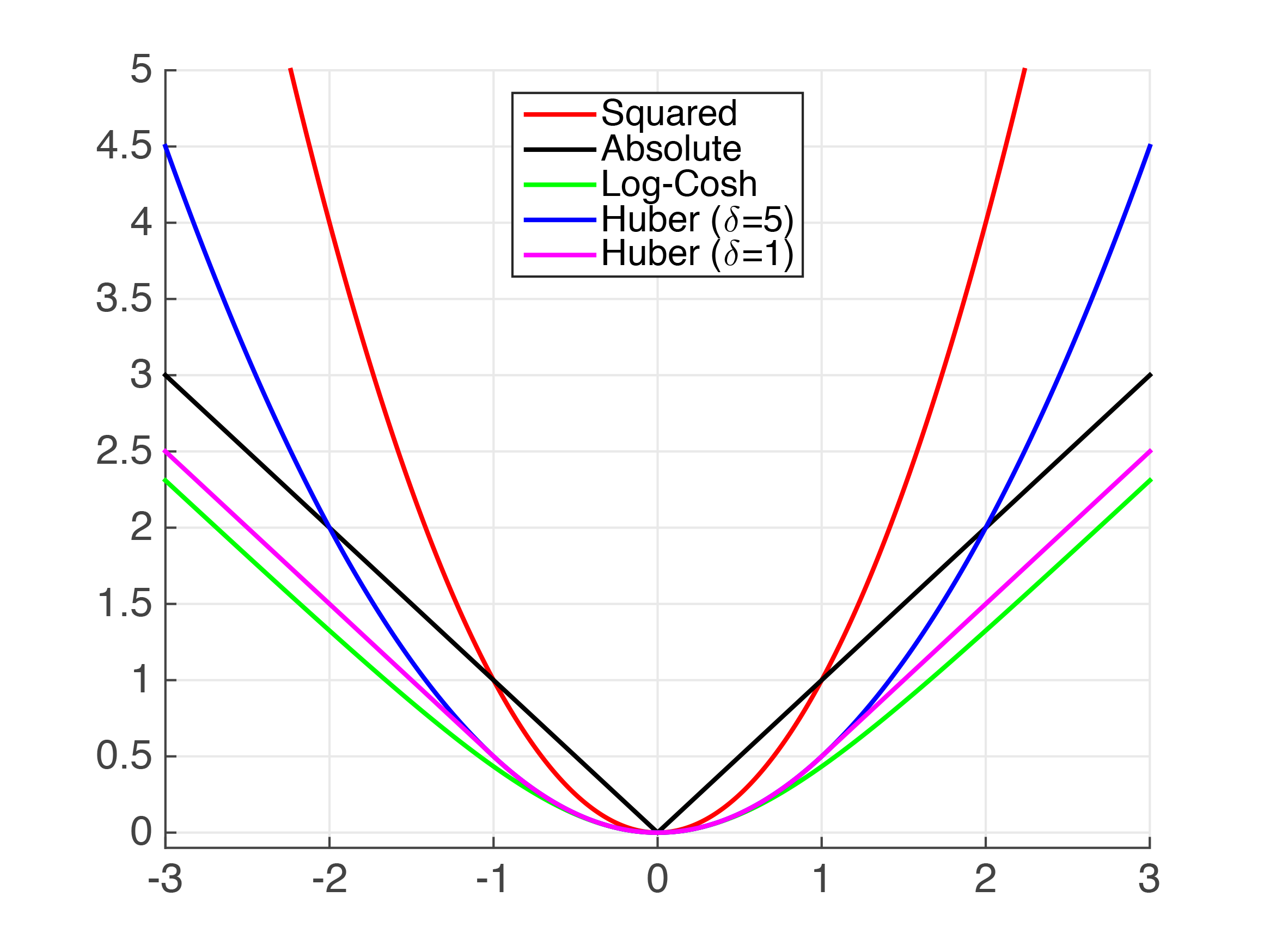
横坐标：$h(\mathbf{x}_{i})y_{i}$ 或者预测的'error' | 纵坐标：损失值

（1）MSE与MAE

直观来说，我们可以像这样考虑：对所有的观测数据，如果我们只给一个预测结果来最小化MSE，那么该预测值应该是所有目标值的均值。但是如果我们试图最小化MAE，那么这个预测就是所有目标值的中位数。我们知道中位数对于离群点比平均值更鲁棒，这使得MAE比MSE更加鲁棒。 如果离群点是会影响业务、而且是应该被检测到的异常值，那么我们应该使用MSE。另一方面，如果我们认为离群点仅仅代表数据损坏，那么我们应该选择MAE作为损失。

具体实现：

mae和mse的损失值

# 1.调用sklearn
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error

# 2.自定义
def mae_metric(y_true, y_pred):
    return 'mae', np.mean(np.abs(y_true - y_pred)), False

def mse_metric(y_true, y_pred):
    return 'mse', np.mean((y_true - y_pred) ** 2), False　

mae和mse的一阶导数和二阶导数：

def mae_loss(y_true, y_pred):
    x = y_pred - y_true
    grad = np.sign(x)
    hess = np.zeros_like(x)
    return grad, hess # 一阶，二阶导数


def mse_loss(y_true, y_pred):
    x = y_pred - y_true
    grad = x
    hess = np.ones_like(x)
    return grad, hess # 一阶，二阶导数

mae和fair loss、huber loss结合

def mae_fair_metric(y_true, y_pred, fair_c):
    # 损失值
    x = y_pred - y_true
    tmp = np.abs(x) / fair_c
    fair = fair_c ** 2 * (tmp - np.log(tmp + 1))
    mae = np.abs(x)
    return 'mae_fair%d' % fair_c, np.mean(0.5 * fair + 0.5 * mae), False

def mae_huber_metric(y_true, y_pred, huber_delta):
    # 损失值
    x = y_pred - y_true
    huber = pseudo_huber_metric(y_true, y_pred, huber_delta)[1]
    mae = np.abs(x)
    return 'mae_huber%d' % huber_delta, np.mean(0.5 * huber + 0.5 * mae), False

def mae_fair_loss(y_true, y_pred, fair_c):
　　# 返回一阶、二阶导数
    grad_mae, hess_mae = mae_loss(y_true, y_pred)
    grad_fair, hess_fair = fair_loss(y_true, y_pred, fair_c)
    grad = 0.5 * grad_mae + 0.5 * grad_fair
    hess = 0.5 * hess_mae + 0.5 * hess_fair
    return grad, hess

def mae_huber_loss(y_true, y_pred, huber_delta):
　　# 返回一阶、二阶导数
    grad_mae, hess_mae = mae_loss(y_true, y_pred)
    grad_huber, hess_huber = pseudo_huber_loss(y_true, y_pred, huber_delta)
    grad = 0.5 * grad_mae + 0.5 * grad_huber
    hess = 0.5 * hess_mae + 0.5 * hess_huber
    return grad, hess

（2）Huber loss 平滑的平均绝对误差

　　可能会出现这样的情况，即任何一种损失函数都不能给出理想的预测。例如，如果我们数据中90％的观测数据的真实目标值是150，其余10％的真实目标值在0-30之间。那么，一个以MAE为损失的模型可能对所有观测数据都预测为150，而忽略10％的离群情况，因为它会尝试去接近中值。同样地，以MSE为损失的模型会给出许多范围在0到30的预测，因为它被离群点弄糊涂了。这两种结果在许多业务中都是不可取的。

　　Huber Loss对数据离群点的敏感度低于平方误差损失。它在0处也可导。基本上它是绝对误差，当误差很小时，误差是二次形式的。误差何时需要变成二次形式取决于一个超参数，(delta)，该超参数可以进行微调。当 ? ~ 0时， Huber Loss接近MAE，当 ? ~ ∞（很大的数）时，Huber Loss接近MSE。

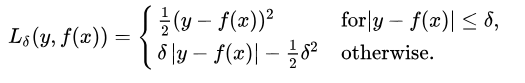
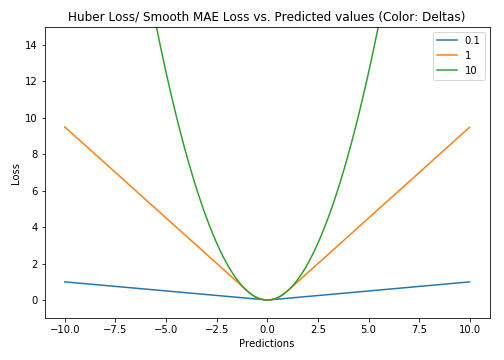
横坐标：预测值 | 纵坐标：Huber loss

　　delta的选择非常重要，因为它决定了你认为什么数据是离群点。大于delta的残差用L1最小化（对较大的离群点较不敏感），而小于delta的残差则可以“很合适地”用L2最小化。

为什么使用Huber Loss？

　　使用MAE训练神经网络的一个大问题是经常会遇到很大的梯度，使用梯度下降时可能导致训练结束时错过最小值。对于MSE，梯度会随着损失接近最小值而降低，从而使其更加精确。

　　在这种情况下，Huber Loss可能会非常有用，因为它会使最小值附近弯曲，从而降低梯度。另外它比MSE对异常值更鲁棒。因此，它结合了MSE和MAE的优良特性。但是，Huber Loss的问题是我们可能需要迭代地训练超参数delta。

具体实现：

def sm_mae(true, pred, delta):
   """
   true: array of true values    
   pred: array of predicted values

   returns: smoothed mean absolute error loss
   """
   loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2))
   return np.sum(loss)

pseudo huber loss:

def pseudo_huber_metric(y_true, y_pred, delta):
    # 损失值
    x = y_pred - y_true
    return 'huber%d' % delta, np.mean(delta ** 2 * (np.sqrt((x / delta) ** 2 + 1) - 1)), False

def pseudo_huber_loss(y_true, y_pred, delta):
　　 # 一阶、二阶导数
    x = y_pred - y_true
    scale = 1 + (x / delta) ** 2
    scale_sqrt = np.sqrt(scale)
    grad = x / scale_sqrt
    hess = 1 / (scale * scale_sqrt)
    return grad, hess

（3）fair loss

来自solution in the Kaggle Allstate Challenge.

def fair_loss(y_true, y_pred, faic_c):
    x = y_pred - y_true
    grad = faic_c * x / (np.abs(x) + faic_c)
    hess = faic_c ** 2 / (np.abs(x) + faic_c) ** 2
    return grad, hess

fair loss和huber loss结合

def fair_huber_loss(y_true, y_pred, fair_c, huber_delta):
    grad_fair, hess_fair = fair_loss(y_true, y_pred, fair_c)
    grad_huber, hess_huber = pseudo_huber_loss(y_true, y_pred, huber_delta)
    grad = 0.5 * grad_fair + 0.5 * grad_huber
    hess = 0.5 * hess_fair + 0.5 * hess_huber
    return grad, hess

（4）Log-Cosh loss

　　Log-cosh是用于回归任务的另一种损失函数，它比L2更加平滑。Log-cosh是预测误差的双曲余弦的对数。

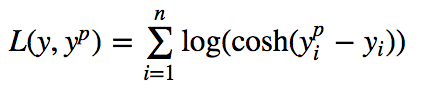
优点： log(cosh(x))对于小的x来说，其大约等于 (x ** 2) / 2，而对于大的x来说，其大约等于 abs(x) - log(2)。这意味着'logcosh'的作用大部分与均方误差一样，但不会受到偶尔出现的极端不正确预测的强烈影响。它具有Huber Loss的所有优点，和Huber Loss不同之处在于，其处处二次可导。

为什么我们需要二阶导数？

许多机器学习模型的实现（如XGBoost）使用牛顿方法来寻找最优解，这就是为什么需要二阶导数（Hessian）的原因。对于像XGBoost这样的机器学习框架，二阶可导函数更有利。

 但Log-chsh Loss并不完美。它仍然存在梯度和Hessian问题，对于误差很大的预测，其梯度和hessian是恒定的。因此会导致XGBoost中没有分裂。

具体实现：

def logcosh(true, pred):
   loss = np.log(np.cosh(pred - true))
   return np.sum(loss)

（5）Quantile Loss（分位数损失）

　　当我们有兴趣预测一个区间而不仅仅是预测一个点时，Quantile Loss函数就很有用。最小二乘回归的预测区间是基于这样一个假设：残差（y - y_hat）在独立变量的值之间具有不变的方差。我们不能相信线性回归模型，因为它违反了这一假设。当然，我们也不能仅仅认为这种情况一般使用非线性函数或基于树的模型就可以更好地建模，而简单地抛弃拟合线性回归模型作为基线的想法。这时，Quantile Loss就派上用场了。因为基于Quantile Loss的回归模型可以提供合理的预测区间，即使是对于具有非常数方差或非正态分布的残差亦是如此。

具体实现：参考这里

举例：

Regression prediction intervals with XGBOOST 不考虑异常值带来的损失，只考虑一定区间内数据的损失。

 

 

 

 

 

 

 

 

 

参考文献：

【1】机器学习中的损失函数 （着重比较：hinge loss vs softmax loss）

【2】机器学习中的基本问题——log损失与交叉熵的等价性

【3】Empirical Risk Minimization

【4】到底该如何选择损失函数？