518. Coin Change 2
原题链接
题目描述
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2]
输出:0
解释:只用面额 2 的硬币不能凑成总金额 3 。
示例 3:
输入:amount = 10, coins = [10]
输出:1
问题分析
先看leetcode官方给的一种 解法
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] += dp[i - coin];
}
}
return dp[amount];
}
}
这种解法给人一种似懂非懂的感觉,反正我一直没记住,到底是应该把 for (int coin : coins) 循环写在外边,还是应该把 for (int i = 0; i <= amount; i++) 循环写在外边。其实你回去试,会发现这两种写法答案不一样,只有上面这种把 for (int coin : coins) 循环写在外边的才是正确的做法。
这里不去解释为什么两种写法不一样,详细解释可见这里👉 零钱兑换II和爬楼梯问题到底有什么不同?
我们从形式上看,这个问题是用dp来做的,这里是一个二层循环,传统的dp问题如果用到的是二层循环,一般是二维dp,但是这却只用了一个一维数组,让人不清楚这到底是一维dp还是二维dp。
于是下面我给出一个更好理解的解法,至少我个人是觉得比上面leetcode官方代码好理解。先看我的代码:
class Solution {
public:
int change(int amount, vector<int>& coins) {
int n = coins.size();
vector<vector<int>> dp(n, vector<int>(amount + 1, 0)); //dp[i][j] 表示可用硬币为 0...i 时,能组成金额j的可能数
//初始化边界条件
//当需要凑出金额为0,其实这里不能说无法凑出,其实每个硬币都不选也是一种方案,题目里并没有说一定要使用硬币。
//或者你可以去试一下,当amount==0的时候,无论可选硬币是什么,都只有一种组合方式,就是所有硬币一个都不选,或者说选一个空集。
for (int i = 0; i < n; i++) dp[i][0] = 1;
//当可选硬币只有第一个的时候,能不能凑出来amount就很简单,只要amount大于等于coins[0],并且是coins[0]的整数倍就行,如果满足这种情况,那么组合数为1,否则还是默认的0
for (int j = 1; j <= amount; j++) dp[0][j] = (j >= coins[0] && j % coins[0] == 0) ? 1 : 0;
for (int i = 1; i < n; i++) {
for (int j = 1; j <= amount; j++) {
if (j >= coins[i]) dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]];
else dp[i][j] = dp[i - 1][j];
}
}
return dp[n - 1][amount];
}
};
这里解释一下上面的状态转移方程
当目前可选硬币从[0 ... i-1] 变成 [0...i] 的时候,言外之意就是说,这一次第i个硬币也是可选的了。
这个时候我们看一下该如何计算 dp[i][j],即当前可选硬币是[0...i]的时候,要凑出j一共有多少种方案?
其实这里有一个问题?就是凑出 j 会不会用到第i个硬币?
什么时候可能用到第i个硬币,那肯定是 j >= coins[i] 的时候可能会用到,否则的话是用不到的,用不到的意思就是说,你现在计算dp[i][j],其实它的值就等于dp[i-1][j]。
那么当可以用到的时候,该如何计算dp[i][j],注意,我们这里是可以用,但是我们不一定是必须要使用coins[i]才能凑出j,所以dp[i][j] 有一部分是dp[i-1][j];
同时,如果这次用了,那么还要加上dp[i][j - coins[i]]。这里必须强调一下,不是加上dp[i-1][j - coins[i]],为什么呢?因为硬币可以用无数次,你用了coins[i]之后,相当于现在需要使用[0 ... i]这些硬币去凑出 j - coins[i]。如果题目规定每个硬币最多用一次,那这里就是加上dp[i-1][j - coins[i]]。
然后我想回到最开始的那种解法,我们知道,那种解法是不能调换内外两层循环,我们想一下,我这里这种解法可以调换吗?换句话说,其他部分不变,把
for (int i = 1; i < n; i++) {
for (int j = 1; j <= amount; j++) {
...
}
}
变成
for (int j = 1; j <= amount; j++) {
for (int i = 1; i < n; i++) {
...
}
}
其实这里就回到了所有dp问题都需要思考的问题,即,如何确定不同状态的计算顺序。
那么,一个dp问题是如何确定不同状态的计算顺序呢?没错,就是通过状态转移方程来看状态之间的依赖关系。简单来说,当a状态依赖于b状态值的时候,必须找到一种计算顺序,在这种计算顺序下,我们是先计算b的值,再计算a的值。
那么,我们看一下本题的状态转移方程
if (j >= coins[i]) dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]];
else dp[i][j] = dp[i - 1][j];
我们发现,dp[i][j] 这个状态值依赖于dp[i - 1][j] 和 dp[i][j - coins[i]] 这两个状态值,dp[i - 1][j] 是dp[i][j]上一行同一列的位置的值,dp[i][j - coins[i]]是dp[i][j]同一行左边的值,所以,你会发现,以下两种计算顺序都符合这种状态之间的依赖关系。
-
从第一行到最后一行,每行从左到右计算
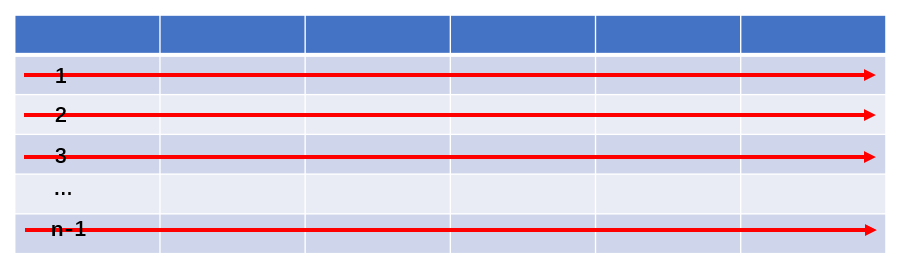
-
从第一列到最后一列,每列从上到下计算

所以我们这种方式是可以交换内外层循环的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号