Stanford机器学习---第六讲. 怎样选择机器学习方法、系统
原文:http://blog.csdn.net/abcjennifer/article/details/7797502
本栏目(Machine learning)包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM(Support Vector Machines 支持向量机)、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew老师的讲解。(https://class.coursera.org/ml/class/index)
第六讲. 怎样选择机器学习方法——Advice for applying machine learning
===============================
候选机器学习方法
评价方法假设
☆模型选择和训练、验证实验数据
☆区别诊断偏离bias和偏差variance
☆规则化 和 bias/variance
Learning Curve:什么时候增加训练数据training set才是有效的?
===============================
候选机器学习方法——Deciding what to try next
还用房价的prediction举例,假设我们已经实现了用规则化的线性回归方法预测房价:
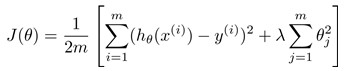
但发现该预测应用于一个新的训练数据上时有很大误差(error),这时应采取一些解决方案:
Machine Learning 方法的诊断:
- 什么是诊断Dignostic呢?诊断就是能够判断一种学习算法能不能work,并且改善该算法性能的一个测试。
Diagnostic: A test that you can run to gain insight what is/isn't working with a learning algorithm, and gain guidance as to how best to improve its performance.
-诊断的效果:Diagnostics can take time to implement, but doing so can be a very good use of your time.

===============================
评价方法假设——Evaluating a hypothesis
首先呢,我们将所有数据分为两个集合,一个Trainning set和一个Testing set,用Training set得到参数向量,用Testing set进行测试(比如分类)。

这时,将test set的error分为线性回归linear regression和逻辑回归logistic regression两类:
-线性回归的error:

-逻辑回归的error:
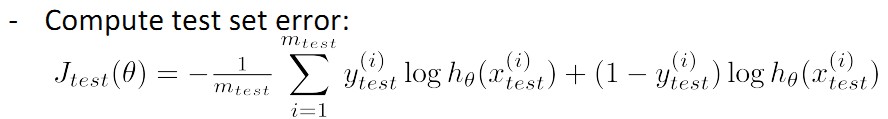
===============================
模型选择和训练、验证实验数据
面对模型选择问题,如何才能得到一个just fit的模型而不会导致underfit 或者overfit呢?我们引入一类数据集,叫做cross validation set,即交叉验证数据集。将所有数据按<6,2,2>分为training set , cross validation set , testing set三类,如下图所示:

其error计算公式如下,其实三类计算方法大同小异,相同的公式只是换了数据及而已:

进行模型选择的方法其实很简单,对应下图大家来看:
-首先,建立d个model 假设(图中有10个,d表示其id),分别在training set 上求使其training error最小的θ向量,那么得到d个θ
-然后,对这d个model假设,带入θ,在cross validation set上计算J(cv),即cv set error最小的一个model 作为 hypothesis,如下图中J(cv)在第4组中最小,便取d=4的假设。
PS: 其实d表示dimension,也就是维度,表示该hypothesis的最大polynomial项是d维的。
PS': 一般地,J(cv)是大于等于J(train)的

===============================
区别诊断偏离bias和偏差variance
前面的课程中我们曾讲过相同数据不同回归情况:

这一节中,我们给大家区分两个概念:bias vs. variance。
如下图所示为error随不同dimension的model变化图,可以想见,随d上升是一个由underfit到overfit的过程,这个过程中,training set的error逐渐下降,而cv set的error先降后升。
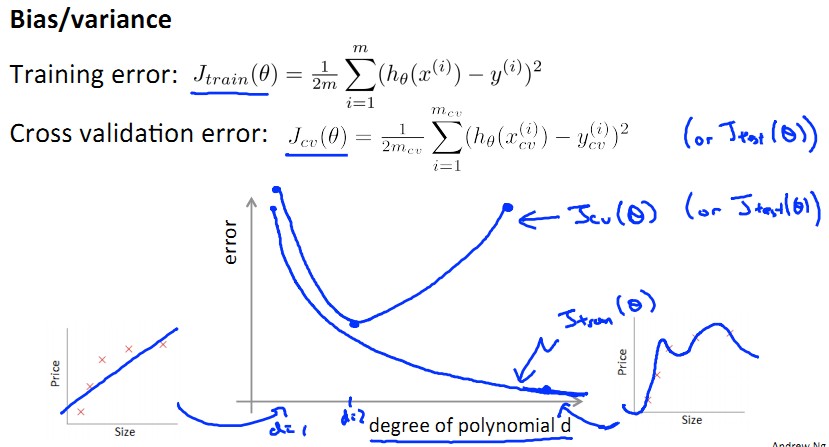
这里就产生了bias和variance的概念:
bias:J(train)大,J(cv)大,J(train)≈J(cv),bias产生于d小,underfit阶段;
variance:J(train)小,J(cv)大,J(train)<<J(cv),variance产生于d大,overfit阶段;
如下图所示:

来来,做道题:

-------------------------------------------------------------
好,有了初步概念,现在我们来看bias和variance的由来及具体定义:
给定数据及D(比如一个点集吧),对于这些数据集上的点我们可以计算每个index下点的平均值(即期望)t(x) = E(y|x),则我们有mean square error:


定义上是这么讲的:
Variance: measures the extent to which the solutions for individual data sets vary around their average, hence this measures the extent to which the function f(x) is sensitive to theparticular choice of data set.
Bias: represents the extent to which the average prediction over all data sets differs from the desired regression function.
Our goal is to minimize the expected loss, which we havedecomposed into the sum of a (squared) bias, a variance, and a constant noiseterm. As we shall see, there is a trade-off between bias and variance, with very flexible models(overfit) having low bias and high variance, and relatively rigid models(underfit) having high bias and low variance
总结一下:
variance:估计本身的方差。
bias:估计的期望和样本数据样本希望得到的回归函数之间的差别。
具体来讲,我有一个统计量D(比如统计某大学研一学生身高在[0.5-1],[1,1.1],[1.1,1.2]……[1.9,2]之间的人数),这样可以形成一些离散点。然后呢,本校研一有20个班,每个班就都可以拟合成一条估计曲线f(x),这20条曲线呢,有一个平均值,也就是估计期望(均值)曲线E(f(x,D))。
variance是指,这20条估计曲线与最后估计期望(均值)之间的距离,也就是估计曲线本身的方差,是不可能为0的。
bias是指,20条估计曲线的均值与实际最佳拟合情况之间的距离。
这样一来呢,对于regularization项中的λ,
λ小 , d大 -> overfit(flexible) ->
对于不同的训练数据集(不同班级的数据)的拟合结果抖动很大 -> variance大
bias是估计均值与实际值期望的偏差 -> bias小
下图中,左图为拟合的20条曲线;右图红线为20条曲线的期望,绿色为实际数据期望所得的拟合曲线。

λ大 , d小 -> underfit(stable) ->
对于不同的训练数据集(不同班级的数据)的拟合结果抖动较小 -> variance小
bias是估计均值与实际值期望的偏差 ,不能很好地进行回归-> bias大
下图中,左图为拟合的20条曲线;右图红线为20条曲线的期望,绿色为实际数据期望所得的拟合曲线。

下图所示为λ与bias, variance, error之间的关系:

我们希望的数据的variance和bias都不要大:

那么着就是一个variance和bias之间的tradeoff 了~
===============================
规则化 和 bias/variance
上面一节中讲了bias和variance的诞生,那么这一节中偶们就将他们应用于regularization中。
大家还记的什么是regularization么?regularization就是为了防止overfit而在cost function中引入的一个分量。
还不清楚?看下图吧,regularization项就是cost function J(θ)中的最后一项,其中λ太大导致underfit,λ太小导致overfit……
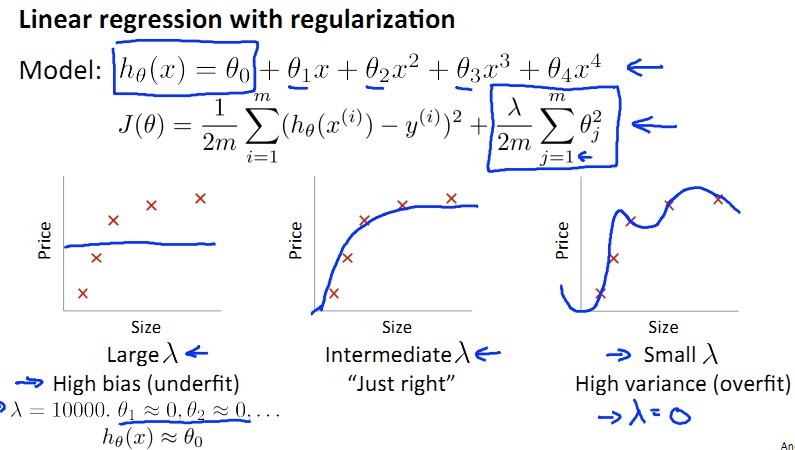
将λ从0,0.01,一直往上每次乘以2,那么到10.24总共可以试12次λ。
这12个λ会得到12个model的 cost function,每个对应有J(θ)和 Jcv(θ).
和模型选择的方法相同,首先选出每个cost function下令J(θ)最小的θ,然后取出令Jcv(θ)最小的一组定为最终的λ。

来来,看看你做的对不:

图画出来就是这个样子滴:

λ太小导致overfit,产生variance,J(train)<<J(cv)
λ太大导致underfit,产生bias,J(train) ≈ J(cv)
能明白我的意思么?
===============================
Learning Curve:什么时候增加训练数据training set才是有效的?
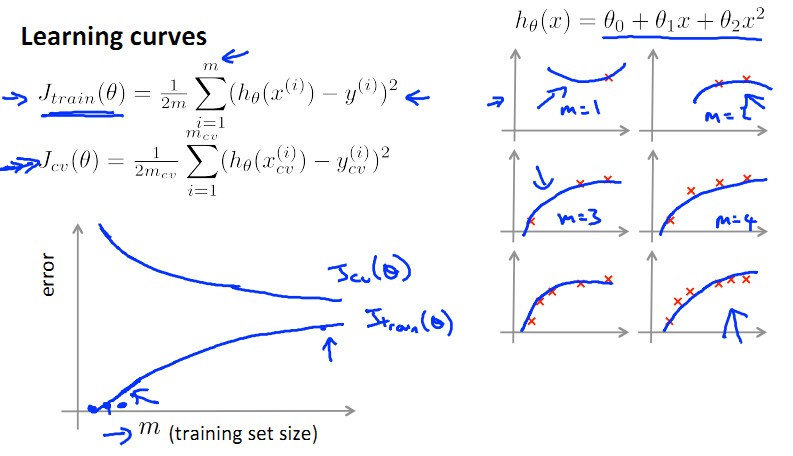
这一小节想要讲讲训练数据个数m和error之间的关系。从上面这幅图中我们可知(不知的话用极限思维想想),训练数据越少(如果只有一个),J(train)越小,J(cv)越大;m越大,J(train)越大(因为越难perfectly拟合),J(cv)越小(因为越精确),懂我的意思吧?
那么我们分别就High Bias 和 High Variance来看看增加training set个数,即m,是否有意义?!
Underfit 的 High bias: 增加m无济于事!
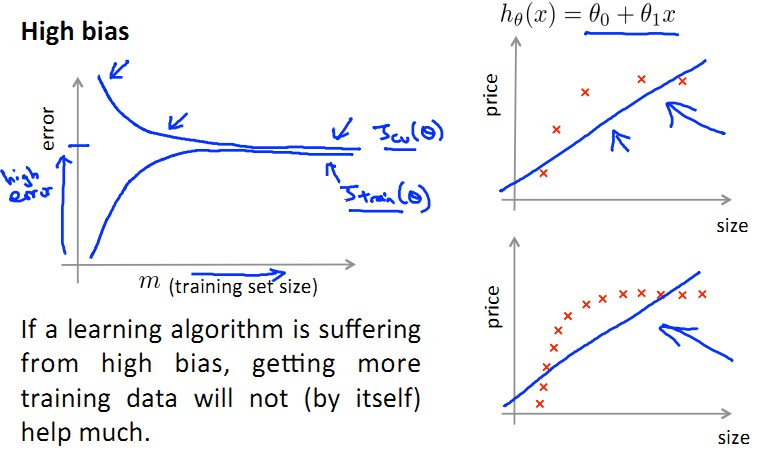
Overfit的 High Variance: 增加m使得J(train)和J(cv)之间gap减小,有助于performance提高!
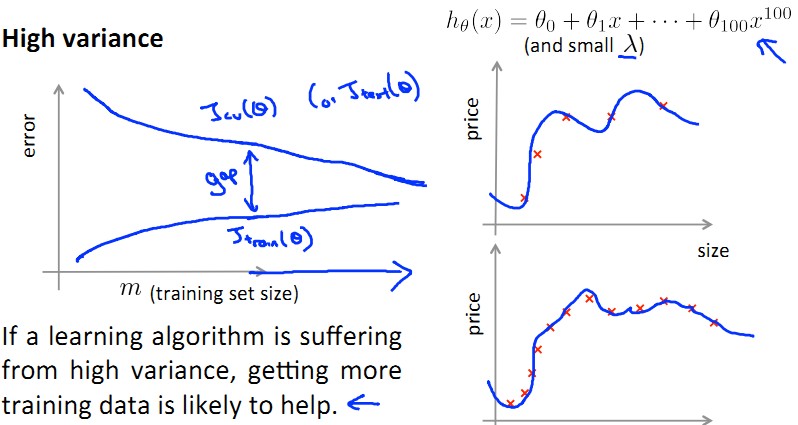
来来,做道题:

由图中可见,增加训练数据的个数对于过拟合是有用的,对于underfit是徒劳!
下面总结一下,重温最初的解决方案列表:

针对underfit和overfit,分别是什么情况呢?见下图:
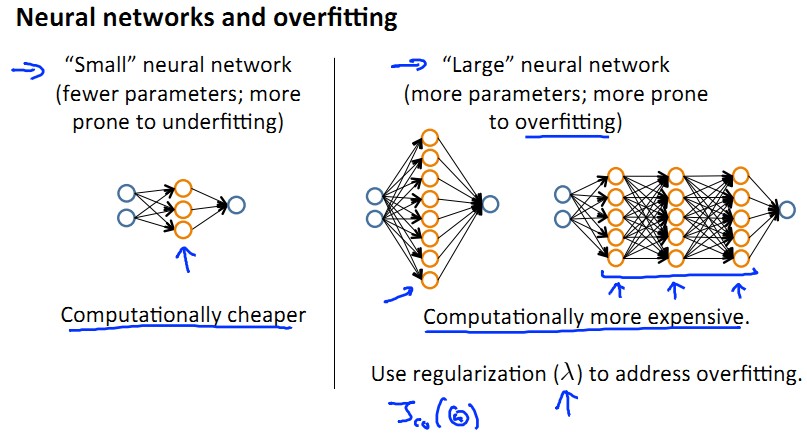
这章非常有用,讲了选择最佳拟合model的问题,是machine learning的常见问题,希望能对大家选择ml 模型有所帮助。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号