[leetcode刷题]——位运算
理论知识参考_CyC大佬总结
基本原理
0s 表示一串 0,1s 表示一串 1。
x ^ 0s = x x & 0s = 0 x | 0s = x
x ^ 1s = ~x x & 1s = x x | 1s = 1s
x ^ x = 0 x & x = x x | x = x
利用 x ^ 1s = ~x 的特点,可以将一个数的位级表示翻转;利用 x ^ x = 0 的特点,可以将三个数中重复的两个数去除,只留下另一个数。
1^1^2 = 2
利用 x & 0s = 0 和 x & 1s = x 的特点,可以实现掩码操作。一个数 num 与 mask:00111100 进行位与操作,只保留 num 中与 mask 的 1 部分相对应的位。
01011011 &
00111100
--------
00011000
利用 x | 0s = x 和 x | 1s = 1s 的特点,可以实现设值操作。一个数 num 与 mask:00111100 进行位或操作,将 num 中与 mask 的 1 部分相对应的位都设置为 1。
01011011 |
00111100
--------
01111111
位与运算技巧
n&(n-1) 去除 n 的位级表示中最低的那一位 1。例如对于二进制表示 01011011,减去 1 得到 01011010,这两个数相与得到 01011010。
01011011 &
01011010
--------
01011010
n&(-n) 得到 n 的位级表示中最低的那一位 1。-n 得到 n 的反码加 1,也就是 -n=~n+1。例如对于二进制表示 10110100,-n 得到 01001100,相与得到 00000100。
10110100 &
01001100
--------
00000100
n-(n&(-n)) 则可以去除 n 的位级表示中最低的那一位 1,和 n&(n-1) 效果一样。
移位运算
\>\> n 为算术右移,相当于除以 2n,例如 -7 \>\> 2 = -2。
11111111111111111111111111111001 >> 2
--------
11111111111111111111111111111110
\>\>\> n 为无符号右移,左边会补上 0。例如 -7 \>\>\> 2 = 1073741822。
11111111111111111111111111111001 >>> 2
--------
00111111111111111111111111111111
<< n 为算术左移,相当于乘以 2n。-7 << 2 = -28。
11111111111111111111111111111001 << 2
--------
11111111111111111111111111100100
![]()
mask 计算
要获取 111111111,将 0 取反即可,~0。
要得到只有第 i 位为 1 的 mask,将 1 向左移动 i-1 位即可,1<<(i-1) 。例如 1<<4 得到只有第 5 位为 1 的 mask :00010000。
要得到 1 到 i 位为 1 的 mask,(1<<i)-1 即可,例如将 (1<<4)-1 = 00010000-1 = 00001111。
要得到 1 到 i 位为 0 的 mask,只需将 1 到 i 位为 1 的 mask 取反,即 ~((1<<i)-1)。
Java 中的位操作
static int Integer.bitCount(); // 统计 1 的数量
static int Integer.highestOneBit(); // 获得最高位
static String toBinaryString(int i); // 转换为二进制表示的字符串
一、统计两个数的二进制表示有多少位不同
461.汉明距离 (easy) 2021-01-24
两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。
给出两个整数 x 和 y,计算它们之间的汉明距离。
注意:
0 ≤ x, y < 231.示例:
输入: x = 1, y = 4
输出: 2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑上面的箭头指出了对应二进制位不同的位置。
本菜鸡也能一行解决了, 哈哈哈哈哈哈。
public int hammingDistance(int x, int y) { return Integer.bitCount(x ^ y); }
二、数组中唯一一个不重复的元素
136. 只出现一次的数字 (easy) 2021-01-24
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
首先设置一个0,然后遍历做异或运算,相同的数异或会为0,然后最后就会剩下只出现了一次的数。
class Solution { public int singleNumber(int[] nums) { int res = 0; for(int i : nums){ res = res ^ i; } return res; } }
三、找出数组中缺失的那个数
268.丢失的数字
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
进阶:
你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?
示例 1:
输入:nums = [3,0,1]
输出:2
解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
从数学的角度分析,结果就是1-n求和减去nums数组求和。
class Solution { public int missingNumber(int[] nums) { int res = 0; for(int i = 0; i < nums.length; i++){ res = res - nums[i] + i + 1; } return res; } }
异或的效果也是一样。
public int missingNumber(int[] nums) { int ret = 0; for (int i = 0; i < nums.length; i++) { ret = ret ^ i ^ nums[i]; } return ret ^ nums.length; }
四、数组中不重复的两个元素
260. 只出现一次的数字Ⅱ (medium) 2021-01-24
给定一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。
示例 :
输入: [1,2,1,3,2,5]
输出: [3,5]
注意:结果输出的顺序并不重要,对于上面的例子, [5, 3] 也是正确答案。
你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现?
这个题是136题的升级版,上面那个题是整个数组有且只有一个元素出现一次其余均两次,所以将所有的数进行异或运算得到的就是那个只出现了一次的数。
此题有两个数只出现了一次,我们将所有的数进行异或运算得到的是这两个数的异或运算。那么我们将异或结果的最后一个1当作标记(异或结果为1那么两个数在这个位上是一个0一个1),以此将数组一分为二,就成了上面easy题的情况。公式:diff &(-diff) 取最后一个1,-diff = ~diff + 1,(负数在计算机中都是以补码的形式表示的)
这里需要注意,例如int 是4 个字节,一个字节是8个byte, 所以 7 的二进制是(111),-7 的二进制是(11111111111111111111111111111001)。
class Solution { public int[] singleNumber(int[] nums) { int xor = 0; int[] res = new int[2]; for(int num : nums){ xor ^= num; } xor = xor & (- xor); //这里是取两个元素的最后一个1 for(int num : nums){ if((num & xor) == 0) res[0] ^= num; else res[1] ^= num; } return res; } }
五、翻转一个数的比特位
190. 颠倒二进制位 (easy) 2021-01-24
颠倒给定的 32 位无符号整数的二进制位。
示例 1:
输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596,
因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在上面的 示例 2 中,输入表示有符号整数 -3,输出表示有符号整数 -1073741825。
二进制移位的题做得真的是脑阔痛
六、不用额外变量交换两个整数
a = a ^ b;
b = a ^ b;
a = a ^ b;
七、判断一个数是不是2 的n 次方
231. 2 的幂 (easy) 2021-01-25
给定一个整数,编写一个函数来判断它是否是 2 的幂次方。
示例 1:
输入: 1输出: true解释: 2 的0次幂 = 1
我的垃圾算法,内存占用超10%。
public boolean isPowerOfTwo(int n) { while(n != 0){ if(n == 1) return true; if(n % 2 != 0) return false; n = n / 2; } return false; }
大佬的算法,一行解决,内存超过64%。二进制中只有一个1。
public boolean isPowerOfTwo(int n) { return n > 0 && Integer.bitCount(n) == 1; }
或者是利用这种性质,1000 & 0111 == 0
public boolean isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }
八、判断一个数是不是4的n次方
342. 4 的次幂 (easy) 2021-01-25
给定一个整数,写一个函数来判断它是否是 4 的幂次方。如果是,返回 true ;否则,返回 false 。
整数 n 是 4 的幂次方需满足:存在整数 x 使得 n == 4的 x 次方
进阶: 不使用循环或者递归
需要举一反三呐。二的幂次方的规律是大于0且只有一个1,四的幂次方的规律是大于0且只有一个1并且 这个1只出现在奇数位。
0b 开头表示二进制。
public boolean isPowerOfFour(int n) { return n > 0 && (n & (n - 1)) == 0 && (n & 0b01010101010101010101010101010101) != 0; }
九、判断一个数的位级表示是否不会出现连续的0和1
693. 交替位的二进制数 (easy) 2021-01-25
给定一个正整数,检查它的二进制表示是否总是 0、1 交替出现:换句话说,就是二进制表示中相邻两位的数字永不相同。
找规律找规律,如果将这样的二进制数向右移位,然后与之做异或运算,就会得到111111111。最后自己与自己加1做与运算可以得到0。
public boolean hasAlternatingBits(int n) { int i = (n ^ (n >> 1)); //会得到一个全为1的二进制 return (i & (i + 1)) == 0; }
十、求一个数的补码
476. 数字的补数 (easy)
给定一个正整数,输出它的补数。补数是对该数的二进制表示取反。
例如 5 的二进制是 101 , 只需要找到 111 去与之做异或运算就行了。难点就在于找到二进制的位数,然后找到与之对应的掩码。
可以使用下列的代码,也可以使用Java封装的函数 Integer.highestOneBit( ), 找出最高位的1,左移然后减一就行。
public int findComplement(int num) { int temp = num, c = 0; while(temp > 0){ temp = temp >> 1; c = (c << 1) + 1; } return num ^ c; }
十一、实现整数的加法
371. 两整数之和 (easy) 2021-01-25
不使用运算符 + 和 - ,计算两整数 a 、b 之和。
示例 1:
输入: a = 1, b = 2
输出: 3
算法原理在于在当前的位置做异或运算,然后与运算进位与之相加。然后使用递归的方法。
public int getSum(int a, int b) { return b == 0 ? a : getSum((a ^ b), (a & b) << 1); }
十二、字符串数组最大乘积
318. 最大单词长度乘积 (medium) 2021-01-25
给定一个字符串数组 words,找到 length(word[i]) * length(word[j]) 的最大值,并且这两个单词不含有公共字母。你可以认为每个单词只包含小写字母。如果不存在这样的两个单词,返回 0。
示例 1:
输入: ["abcw","baz","foo","bar","xtfn","abcdef"]
输出: 16
解释: 这两个单词为 "abcw", "xtfn"。
这个题我是完全没有思路,真真真真太难了。
正确思路说明:因为每个单词只包含26小写字母,所以可以使用32个bit的整形来表示,将两个二进制的数做与运算就可以对比是否有字母重复。然后遍历相乘得到结果。
public int maxProduct(String[] words) { int len = words.length; int[] arr = new int[len]; for(int i = 0; i < len; i++){ for(char j : words[i].toCharArray()){ arr[i] |= 1 << j - 'a'; } } int ret = 0; for(int i = 0; i < len; i++){ for(int j = i + 1; j < len; j++){ if((arr[i] & arr[j]) == 0){ ret = Math.max(ret, words[i].toCharArray().length * words[j].toCharArray().length); } } } return ret; }
十三、统计0-N 中每个数的二进制表示中1 的个数
338. 比特位计数 (medium) 2021-01-26
给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回。
示例 1:
输入: 2
输出: [0,1,1]
进阶:
给出时间复杂度为O(n*sizeof(integer))的解答非常容易。但你可以在线性时间O(n)内用一趟扫描做到吗?
要求算法的空间复杂度为O(n)。
你能进一步完善解法吗?要求在C++或任何其他语言中不使用任何内置函数(如 C++ 中的 __builtin_popcount)来执行此操作。
Java中Integer的静态函数 Integer. bitCount( ) 作用是计算二进制数中 1 的数量。源码如下:
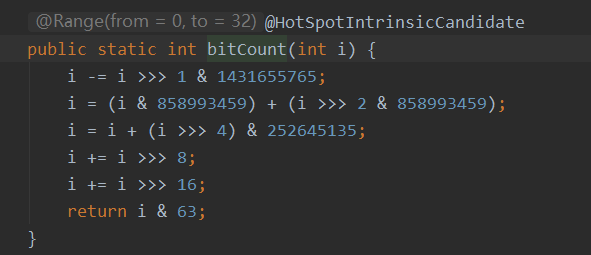
这......完全看不懂好吧。
算法思想,i & (i - 1)的意义就是去除 i 二进制数的最右边的一个 1 ,而且这个数小于 i 就已经保存到数组中了,直接加一就行了。
public int[] countBits(int num) { int[] ret = new int[num + 1]; for(int i = 1; i <= num; i++){ //注意这里是从1 开始,ret[0]取默认值 ret[i] = ret[i & (i - 1)] + 1; } return ret; }







 浙公网安备 33010602011771号
浙公网安备 33010602011771号