关于Focal Loss【转自以学习、回忆】
是解决样本不均衡问题的一种方法,面试常问,但是自己一知半解 遂寻文学习
来源:CSDN GHZhao_GIS_RS
链接:https://blog.csdn.net/u014311125/article/details/109470137
转载一篇以学习、回忆。
转载正文开始 有删减
个人觉的要真正理解Focal Loss,有三个关键点需要清楚,分别对应基础公式,超参数α,超参数γ。
一、二分类(sigmoid)和多分类(softmax)的交叉熵损失表达形式是有区别的。
二、理解什么是难分类样本,什么是易分类样本?搞清难易分类样本是搞清楚Focal Loss中的超参数γ作用的关键。
三、负样本的α值到底该是0.25还是0.75呢?这个问题对应Focal Loss中的超参数α的调参。
理解上面三点应该就能搞清楚二分类Focal Loss的基本思想,然后就可以推广到多分类问题上。
理解关键点一:基础公式
二分类和多分类的交叉熵的区别具体可以参考文章《一文搞懂交叉熵损失》(https://www.cnblogs.com/wangguchangqing/p/12068084.html#autoid-0-2-0)
1.1、二分类交叉熵
在做二分类的任务时,一般是用sigmoid作为最后的激活函数,输出只有一个代表样本为正的概率值p,二分类非正即负,所以样本为负的概率值为1-p。
则以sigmoid作为激活函数的二分类任务交叉熵损失的计算公式为: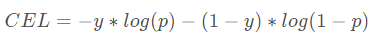
1.2、多分类交叉熵
在做多分类的时候,一般是以softmax作为最后的激活函数的,输出有多个值,对应每个分类的概率值,和为1。
则以sofmax作为激活函数的多分类任务的交叉熵损失计算公式为
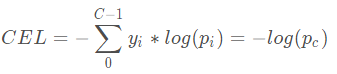
其中p c p_{c}p
c
表示softmax激活函数输出结果中第c类的对应的值。
注意:论文中是基于以sigmoid为激活函数来作为二分类交叉熵损失的。我在最开始学Focal Loss的时候老是将sigmoid和softmax混着看,一会用sigmoid来套公式,一会用softmax来套公式,很容易把自己搞蒙。
文章的备注里也指出可以很容易将Focal Loss应用于多分类,为了简单起见,文章中关注的是二分类情况。
理解关键点二:
![]()
论文将交叉熵损失公式做了进一步的简化:
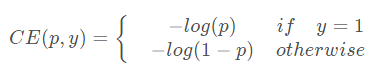
其中
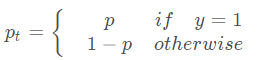
所以:
![]()
这里pt的理解比较关键。pt的大小实际能反映出样本难易分类的程度。举个例子,当样本为正样本(y=1)时,如果模型预测的p=0.3,表示模型预测该样本为负样本,模型预测错误,
pt=0.3,如果模型预测的p=0.8,表示模型预测该样本为正样本,模型预测正确,
pt=0.8。当样本为负样本(y=0)时,如果模型预测的p=0.3,表示模型判断该样本为负样本,判断正确,=1-p=0.7。如果模型输出的p=0.8,表示模型判断该样本为正样本,模型预测错误,pt=1-p=0.2.对应下表
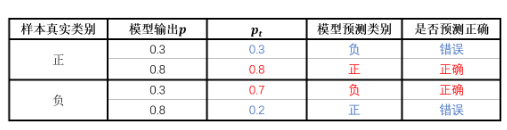
可以看到,不管是正样本还是负样本,模型预测时pt都很大,预测错误时pt很小,所以pt代表了模型对样本预测正确的概率。
接下来看论文中一上来就给的一张图。
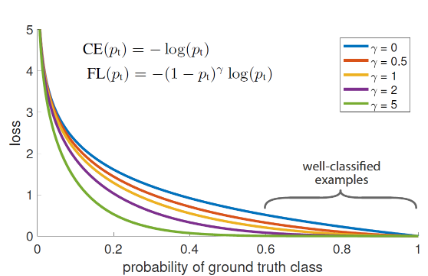
横坐标是pt,可以看出作者指出pt∈(0.6,1)区间为易分类样本。针对上边的例子再啰嗦几句,对于一个正样本,如果模型得到的预测的p总是在0.5以上,则说明该样本很容易被分类正确,所以是易分类样本,此时pt=p,pt也总是在0.5以上,如果模型得到的预测的p总是在0.5以下,则说明该样本很难被正确分类,所以为难分类样本,此时pt也总是在0.5以下;同理对于一个负样本,模型预测的p很容易在0.5以下,表明模型很容易将样本正确分类,所以是易分类样本,pt=1-p,pt总是在0.5以上,如果模型得到的预测的p总是在0.5以上,则说明针对这类样本模型总是分类错误,所以是难分类样本,pt=1-p,pt总是在0.5以下。
总结一下:易分类样本的特征pt>0.5 难分类样本特征:pt<0.5 pt值越大,表示预测越准确。
(自注:这里p值咋来的?怎么判断的Pt 不还是需要p值? 这个p值还是训练过程才能出来吧)
2.2 γ参数
在训练模型的时候,我们希望模型更加关注难分类样本,所以会考虑将难分类样本在损失函数中的比重加大。
作者在原始的二分类交叉熵函数中增加了一项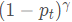 ,对原始交叉熵损失做了衰减。
,对原始交叉熵损失做了衰减。
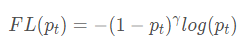
经过对pt的分析可知,难分类样本的pt值小,1-pt大。易分类样本的pt值大,1-pt值小。不管是难分类样本还是易分类样本,Focal Loss相对于原始的CE loss都做了衰减,只是难分类样本相对于易分类样本衰减的少。这里超参数γ决定了衰减的程度。γ损失越大,损失衰减越明显。对上面例子:

理解关键点三:超参数at
我们在做实际模型训练的时候,经常会遇到各类样本数量比例不平衡的情况,对于二分类任务,负样本的数量远远多于正样本,导致模型更多关注在负样本上,忽略正样本。因此在使用交叉熵损失的时候通常会增加一个平衡参数用来调节正负样本的比重。
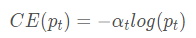
at的定义和pt的定义类似。应该是
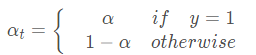
可以知道at代表了正样本的权重,1-at代表了负样本的权重,这两个值应该是正负样本数量比例的反比,如正样本占0.2,负样本数量占0.8。那么at=0.8,1-at=0.2。以词来达到平衡正样本的目的,这样理解看来是没有问题的。
所以Focal Loss的最终表达式:
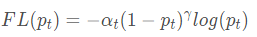
作者指出加入at平衡参数比不加时精度有所提升。给出了实验参数,at=0.25 γ=2时精度最高。这时就有一个问题了。at代表计算损失时正样本的调节权重,而正样本数量一半小于负样本,所以正样本的权重应该大于负样本的权重, 那作者实验中最佳的正样本权重(α {\alpha}α=0.25)为啥比负样本权重(1-α {\alpha}α=0.75)还要低呢?明明负样本的数量已经远远大于正样本的数量了,为啥还要增加损失函数中负样本的比重呢?这不是矛盾吗?
其实作者在论文里给出了解释。有两处:

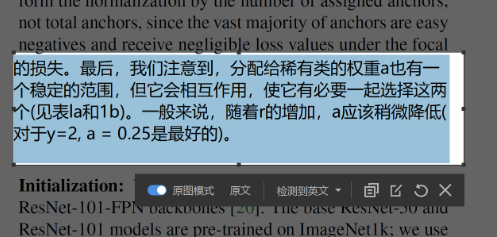
这段有两点信息:
1.at代表了样本数量较少的类的权重,也就是绝大多数情况下的正样本。
2.at与γ是相互作用的,γ增加 a应该稍微降低。

这段话有三点意思:
1.低a对应高γ
2.负样本分类,权重已经被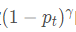 降低很多了,所以无需给正样本再增加权重。
降低很多了,所以无需给正样本再增加权重。
3.Focal Loss种γ占主要地位。
多分类
接下来吧Focal Loss推广到多分类任务中。
接下来我们把Focal Loss推广到多分类任务中,看看多分类中的Focal Loss公式应该是怎样的。
首先我们再来回顾一下二分类的Focal Loss的推导过程,其实就是在CE Loss的基础上增加了两项因子
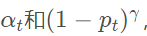 ,其中
,其中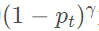 为用来调整难易分类样本的比重,at对经过系数衰减后的损失进行调整。那么
为用来调整难易分类样本的比重,at对经过系数衰减后的损失进行调整。那么
这里就有一个问题了:at和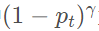 在多分类任务中该怎么表示?
在多分类任务中该怎么表示?
最初的二分类交叉熵损失为:
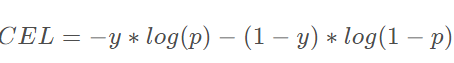
对应的Focal Loss为
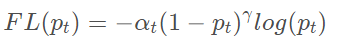
将at pt展开
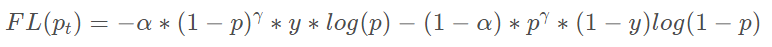
还是二分类,我们把激活函数换成softmax,我们知道sotmax输出的是每个类的概率值,和为1。使用softmax时样本的标签为onehot形式(y1,y2),二分类情况下,第1类标签为(1,0),第二类标签为(0,1).假设softmax输出为(p1,p2)分别对应1,2类的概率。
则以softmax为激活的二分类的交叉熵损失为
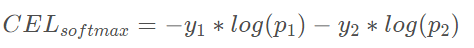
先加入衰减系数γ
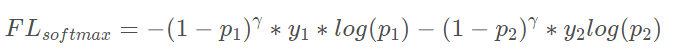
再加入a
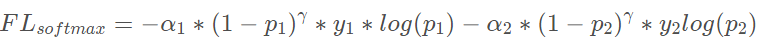
因为标签是onehot形式,某类样本的标签中的只只有再对应位置上为1 其余为0,所以上式写成
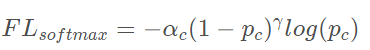
其中ac代表第c类样本的权重,pc代表softmax输出的第c类的概率值


后有代码


 浙公网安备 33010602011771号
浙公网安备 33010602011771号