3D打印路径填充算法 -- Connected Fermat Spirals for Layered Fabrication

本文是笔者在学习这篇论文时的笔记，仅供参考，如需学习，请阅读论文原文献。

这篇文章主要介绍了一种新的打印填充路径 -- 连通的费马螺旋（Connected Fermat Spirals），多数情况下路径连续、低曲率。介绍了该算法的具体实现，然后从打印时间、急转弯个数以及打印质量方面对比本算法与传统的算法，证明了该方法的优势所在。

打印路径的不连续性或者是多轮廓性（discontinuity or contour plurality）会影响喷嘴的开闭，从而影响打印质量和精度；尖锐的转弯和拐角（sharp turns and corners）会减慢打印速度、降低填充质量；

路径填充算法

Zigzag是目前最普遍的打印方法，但是它有许多的急转弯，对于边界复杂或者空心的形状，这个缺点会非常明显。

轮廓平行算法由等间距的平行线组成，可以避免过多的急转弯，但是它导致了较多的轮廓并且轮廓之间不相连。

Hilbert Spiral 通过弯曲保持空间遍历的局部性，然而CFS为保持平滑性尽量避免弯曲。

螺旋填充，对于简单图形来说，是一个连续的曲线；但是对于复杂的图形来说，会造成许多的pocket，如下右图（a）。这些包均不相连从而导致了多路径。

费马螺旋由两个相互交织的子螺旋线组成，一个向内，一个向外。

费马螺旋有一下三个优点：

1）与轮廓平行类似，费马螺旋只在中心处有一个急转弯

2）一些费马螺旋可以连续填充2D区域；传统的螺线要么向内，要么向外，费马螺旋既向内又向外，可以在边界处会合。

3）费马螺旋的起止结点可以在边界处任意选取，便于螺线之间的连接。

连通的费马螺旋算法：

1.将输入区域分解成几个子区域，每个区域可以由一条费马螺旋填充。起止点在边界上紧挨着。

2.遍历子区域，将子区域的起止点相连接，形成一条连续的螺线。

3.进一步的优化以提高平滑性以及空间间隔。

CFS不一定能完全覆盖2D的区域，也不一定具有传统算法所有的优势。

背景及相关内容

背景：最近，提升3D打印的外形以及内部构造非常热门，提升物理稳定性、结构强度、打印的外形、节省材料、适应有限的打印量（improve physical stability [Prevost et al. 2013], structural strength [Stava et al. 2012; ´ Hildebrand et al. 2013; Lu et al. 2014], or appearance [Zhang et al. 2015] of the print, to save material [Vanek et al. 2014b; Hu et al. 2014], and to adapt to the limited print volume [Luo et al. 2012; Vanek et al. 2014a; Chen et al. 2015; Yao et al. 2015]）

这部分主要介绍了填充路径连续以及平滑的重要性、喷嘴结构的构造以及优化填充路径的方法。

填充路径连续性：在开启喷嘴的时候，由于液体的可压缩性，会导致少填充或过填充，造成表面填充不均与影响视觉效果，或者内部不均匀影响结构的强度；关闭喷嘴的时候，由于关闭开关与停止喷墨的时间间隔难以控制，导致填充不均匀。因此，应该最大化填充路径的连续性。

填充路径几何性：急转弯会导致更多的加速或者减速，以及更多的填充不均匀，从而影响打印时间以及质量。

方向平行VS边缘平行：zigzag属于方向平行类，contour-parallel属于边缘平行类，它有更顺畅的转弯和边界，但是有高轮廓性，二者的结合可能会更好，但是连续性有待商榷。

螺旋填充路径：在pocket中应用螺旋较多，但它缺少方向偏差（direction bias），连续性有待优化

空间填充曲线：SFC（Space Fill Curves）指填充2D区域的连续的路径。广泛应用在图像解码，迷宫设计。但是在路径填充中很难实现，急转弯比较多。

迷宫：迷宫也是一种空间填充，本算法也是一种空间填充，只是产生的结果更加的平滑，有更少的急转弯。

域分解：

连续可填充形状：

螺旋、费马螺旋和螺旋性

首先介绍了轮廓平行，然后转化成螺旋，最后转化成费马螺旋。

边界等值的轮廓平行：由间距相等、各不相连，分别平行于边界的线组成

螺旋与螺旋性：通过打断然后重新组合两个相邻的等值线，可以组合成螺旋线，但是有许多包的等值线就不能打断重新组合成一条连续的螺旋线，称之没有螺旋性。

费马螺旋：具有可螺旋性的螺旋曲线能被转化成费马螺旋，并可以任意的选取费马螺旋的起止点（未完待续…详细的还没明白）

连通的费马螺旋填充

这一部分主要描述了如何利用本算法为任意的单一连通2d区域R构造一个连续的CFS填充路径。关键是恰当地重组曲线集合和由区域边界通过欧几里德距离转化过来的ISO-contour。在一个pocket中，rerouting产生一个费马螺旋。在pocket之间或接近分枝的区域，rerouting会连接曲线。

给定路径填充的宽度w，w描述ISO-contour之间的距离，我们使用clipper算法在R上为ISO-contour构建一个集合L。我们以 Ci,j来索引一个ISO-contour，i表示它到区域边界的距离，j是所有具有相同的距离i的iso-contours的索引。比如与就属于不同的pocket。通常情况下，我们令C1，1 是最外层的区域边界接下来我们构建一个spiral-contour tree，节点是iso-contours，与其他iso-contours的带权连接。这个树是一个自底向上的不断递归重组contours的过程。

构造树：

我们首先连接连续的iso-contours，比如以Ci,j 和在一个最初的图中，我们定义一个由 Ci,j 到的连接线段满足。

d（p,c）表示从点p到contour上所有点的距离，片段由这两个ios-c之间所有可能的重组的点组成。如果它不为空的话我们就在图上在， Ci,j 和之间添加一个边，这个边的权重是的长度。一个长的连接片段有可能形成一个长的，低曲率的路径，所以最好不要这样的连接片段上重组。

初始图构建完成后，我们就完成了最小权重生成树，螺旋轮廓树，是树的根

树的节点有两种情况，一种连接到形成螺旋区域的iso-c上的有小于或等于2的度，如图中R0，R1，……，R4由第一种节点组成。第二种节点的度大于2，在上图（b）中蓝色的节点，并且他们与分支iso-c连接在一起。这样的iso-contour为螺旋区域或者其他的第二类结点提供一个接口。

重组：

为了获得一个全局连续的路径，我们以自底向上的方向重组iso-c，从叶节点最后到根节点。有两种重组的操作。第一种是螺旋区域连接iso-c，将他们连成首尾紧邻的单一的费马螺旋。这一部分在section3的后边，如下图所示

第二个操作就是将起止点与最近的第二种类型的iso-c上的点，如图灰色点

尽可能的，重组的点被重复使用，来避免产生新点来代替急转弯。

曲线优化：

目前所获得的是全局连续的，并且覆盖了输入区域R，但是它只是连续，而且可能在spacing上非常不均匀。在后期过程中，我们会局部的优化它的fairness和spacing。当前的曲线是首先采用自适应曲率采样的，以确保在曲率较大出有更多的采样点。优化函数是三个term的加权和：

1． the first term penalizes large perturbations 波动

2. the smoothing term is defined by a chord-length weighted 1D discrete Laplacian平滑项由一个弦长为1D的拉普拉斯算子定义

3. the spacing term keeps shortest distances between adjacent curve segments close to a fixed, pre-defined patch spacing空间项保持相邻曲线间的最短距离接近于事先规定的spacing

优化前后的结果对比如下所示：

结果对比

在同等的条件下（a RepRap Prusa i3 FDM 3D printer with firmware Marlin 1.1.0- RC）实验对比

凹陷以及空心情况下 zigzag VS contour-paraller 通过pocket的数目，急转弯数目，重组点的数目，打印时间等进行衡量优劣。

分别为zigzag contour-paralle CFS的路径数目以及急转弯（小于30%的圆）的个数

Number of tool path segments (#seg) and percentage of sharp turn points (%st),

which we explain in the text, for conventional zigzag (Z), contour-parallel (C), and

our CFS fills (F). The 10 shapes are from the last two rows of Figure 8.

相较于另外两种方法，CFS只有一条路径，急转弯的个数也相对较少。

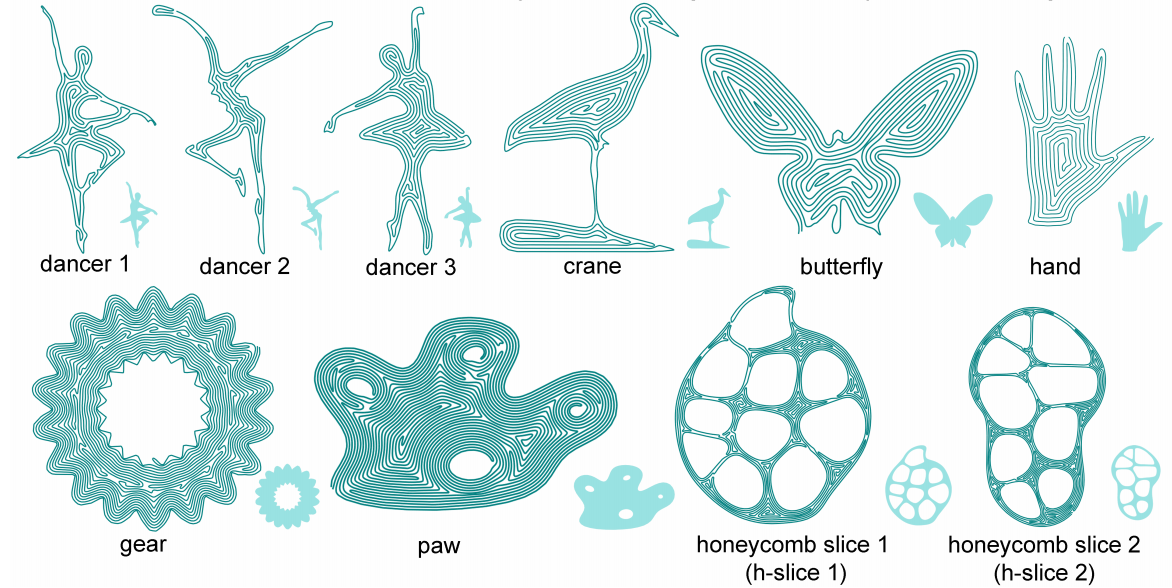
We report the number of pockets (#P) and the number of rerouting points (#R) of the tool

paths. For running times, we report time needed for rerouting to generate the initial

connected Fermat spirals (CFSt) and time for curve optimization (OPt), as well as the total.

All running times are in seconds.

Estimated over- and under-fill rate comparisons on the four shapes from Figure 11.

Top: Before and after curve optimization.

Bottom: comparison between the three fill methods zigzag (Z), contour-parallel (C), and CFS.

（smoothing）平滑会增加空隙以及少填充，优化（smoothing and spacing）会增加少填充，减少过填充，使得更加均匀的填充。

结论、限制以及展望

FDM熔融沉积制造：有两个喷嘴，一个用于沉积制造，一个用于支撑材料。这样制造的物件，垂直于切面的方向不够坚固

附录：

这一部分主要是从三个方面来通过计算优化曲线

the magnitude of the perturbations
smoothness potential
spacing after smoothing

对这三个方面分别定义一个计算公式，然后最终的优化函数就是

利用高斯-牛顿方法对该函数进行优化。

为了制定曲线优化的目标函数，我们通过基于曲率的采样方式来离散化输入的曲线，这样可以在高曲率的地方有更多的采样点。代表一组有序采样点，我们的目标就是打乱这些点，使得路径变得更smoother并且保留着规定的spacing，即相邻两个曲线间的距离应该被fix为d。

在此公式中，主要考虑三个目标。

the magnitude of the perturbations
smoothness potential
spacing after smoothing

第一个目标是the magnitude of the perturbations，由最小二乘法计算

第二个目标叫是smoothness potential。我们修改了中点的定义使其反映密度的变化，确切的，我们定义,然后smoothness potential定义为

（这里使用的是三点位于一条直线上的性质，如果三点位于一条直线上，那么该值为0）。

第三个目标是spacing after smoothing，为了实现这个目的，我们计算每一个点在相邻片段上最接近的点（或者叫footpoint）。对每一个footpoint有两种情况：

1）footpoint落在边上，可以通过 Pj和Pj+1 计算出footpoint;

2）footpoint落在顶点上，并且Ti,j 小于等于0， Ti,j-1大于等于1

？？？

为了计算出在相邻片段上的footpoint，我们选择，不与已经存在的曲线相交。我们定义，两个集合分别包含所有的边footpoint和顶点footpoint。我们将spacing-preserving定义为

将上述三个公式按权重求和，我们就求得了spacing-preserving path smoothing的优化。

在本次实验中，我们令alpha=200，belta=1.0

优化：

目标函数（2）包含既包含一个离散的组件又包含连续的层面，即footpoint的集合和由曲线顶点位置确定的最小二乘。We propose to alternate between updating both，当曲线顶点的位置是固定的，我们就利用上述的方法计算footpoints。当footpoint是固定的时候，我们就应用高斯-牛顿方法去优化（2），根据它非线性最小平方。