正态分布
文章转自:https://zhuanlan.zhihu.com/p/344464677?ivk_sa=1024320u
高斯分布(Gaussian distribution),又名正态分布(Normal distribution),也称"常态分布",也就是说,在正常的状态下,一般的事物,都会符合这样的分布规律. 比如人的身高为一个随机变量,特别高的人比较少,特别矮的也很少,大部分都集中在中等身高. 人的智商也是如此,社会精英毕竟少数,大多都是普通人,虽然我们都知道这是真的,但高斯却能用数学语言去描述这样的现象,有人说它是接近上帝的函数,其厉害之处可见一斑.
一维正态分布
1 定义
若随机变量X服从一个位置参数为μ,尺度参数为σ^2的概率分布. 且其概率密度函数为
(1)�(�)=12��exp(−(�−�)22�2)
则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作X~N(μ, σ^2),读作X服从N(μ, σ^2),或X服从正态分布.
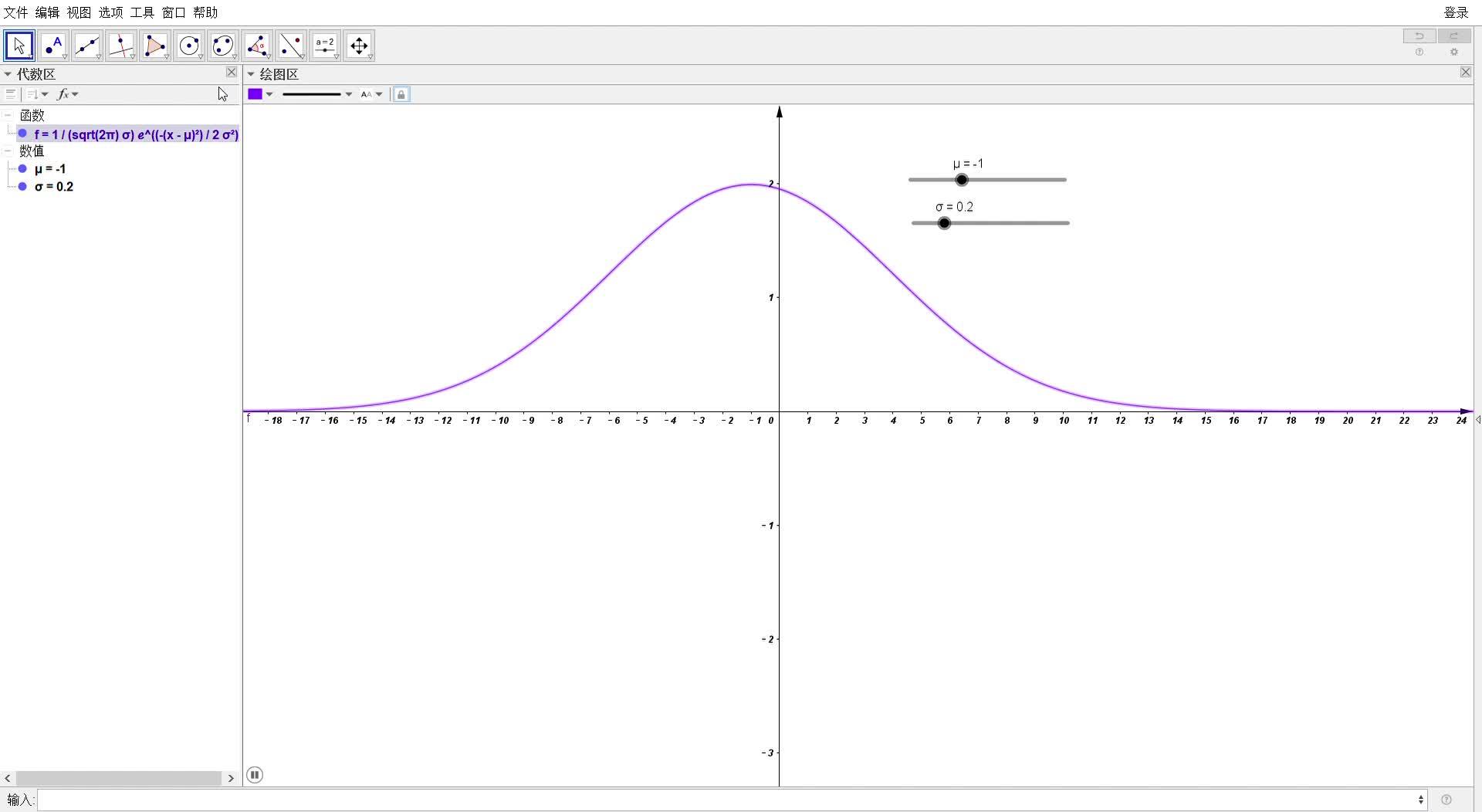
期望值μ决定了正态分布的位置,标准差σ决定了正态分布的幅度.概率密度函数,如图1所示:
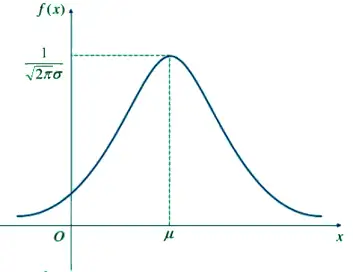
图1 概率密度函数
当μ=0,σ=1时的正态分布是标准正态分布.
(2)�(�)=12�exp(−�22)
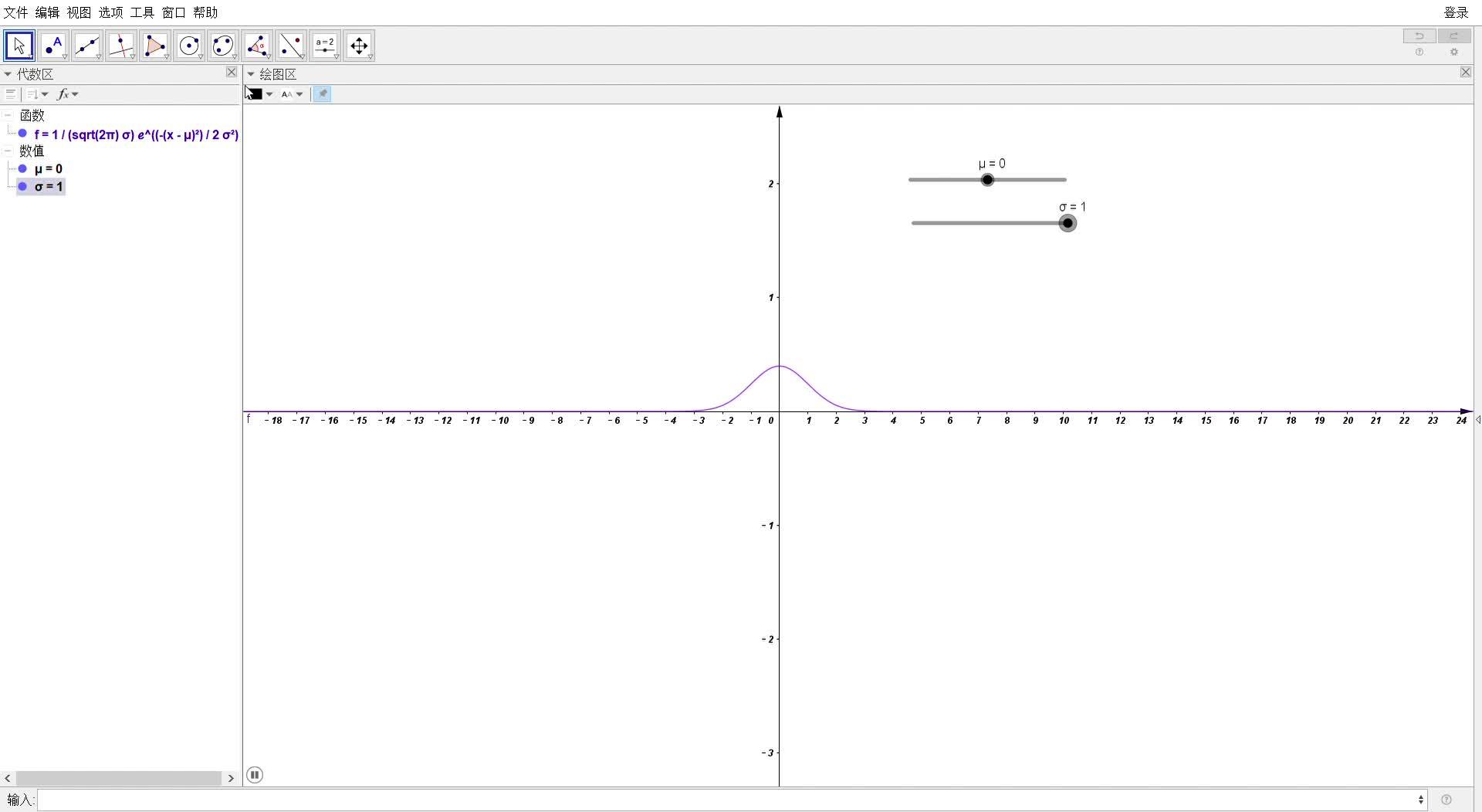
标准差σ反映了数据分布的密集程度,若σ较小,随机变量X分布相对较集中;若σ较大,随机变量X分布相对分散. 如图2所示:
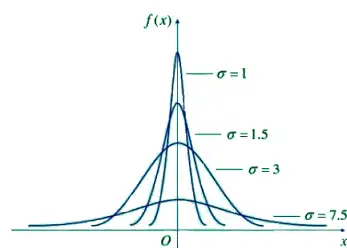
图2 不同σ下的正态分布
2 性质
分布曲线的特征:
- 关于直线 x = μ 对称;
- 在x = μ 处达到最大值;
- 在x = μ±σ处有拐点(凹凸曲线的分界点);
- x → ∞ 时曲线以x轴为渐近线;
- 固定σ,改变μ,则图形沿x轴平移而不改变其形状;
- 固定μ,改变σ,则当σ很小时,曲线的形状与一尖塔相似;当σ值增大时,曲线将趋于平坦.
3 概率分布函数
概率分布函数是正态分布曲线的定积分,公式为:
(3)�(�)=12��∫−∞�exp(−(�−�)22�2)��
① 式(1)中,f(x)表示的概率密度,表示概率在该点的密集程度;
② 实际上,正态曲线与横轴一定区间内所围成的面积反映了变量值落在该区间的概率(概率分布),因此,概率密度函数的积分就是分布函数.
详情可见:0704:概率分布函数、概率密度函数
二维正态分布
1 定义
满足下述的概率密度分布的随机变量分布叫做二维正态分布
(4)�(�,�)=(2��1�21−�2)−1exp[−12(1−�2)((�−�1)2�12)−2�(�−�1)(�−�2)�1�2+(�−�2)2�22]
其中 �1,�2,�1,�2,� 都是常数,我们称 ,(�,�) 服从参数为 �1,�2,�1,�2,� 的二维正态分布,常把这个分布记作 �(�1,�2,�12,�22,�) . �1,�2,�1,�2,� 的范围分别为 −∞<�1<+∞;−∞<�2<+∞;−1<�<1;�1>0;�2>0 .
� 为两个随机变量 ,�,� 的相关系数.
2 应用
- 高斯滤波(Gaussian Filtering)
在图像处理领域中,高斯滤波是一种图像线性平滑的技术,广泛应用于图像处理的减噪等过程. 这里主要说一下高斯核如何形成.
如果对图像滤波技术比较熟悉的话,对均值滤波、中值滤波应该比较了解. 均值滤波对卷积核取相同的权值,而高斯滤波的权值服从高斯分布.
高斯分布主要参数为均值 � 和方差 � , 均值 � 表示中心点的位置,即偏移量,方差 � 则表示向中心点的集中程度,如图3所示, � 越小,数据分布越紧密,向中心点聚集, � 越大,数据越分散,越向两侧发散.
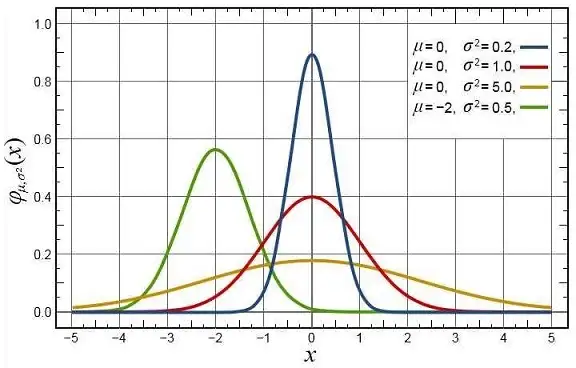
图3 正态分布
图像一般为二维,故通常采用二维高斯滤波,在高斯卷积核中,核中心坐标为(0, 0),如图4所示,为一个3×3的卷积核及各点对应的坐标.

图4 卷积核
卷积核中心点坐标为(0, 0),所以 �1=�2=0 ,由于 ,�,� 相互独立, 相关系数相关系数� 为0,一般情况下, �1=�2=� . 因此,由式(4)可知,二维高斯滤波函数为:
(5)�(�)=12��2exp(−�2+�22�2)
高斯滤波实质上用一个卷积(模板)遍历图像中的每一个像素,这就是卷积的过程,通常采用的卷积核大小为1×1、3×3、5×5、7×7 的卷积核,该卷积核内的每一个点对应的权值服从以中心的二维高斯函数,下面,我们以图4:3×3的卷积核为例,假设 �=1 ,计算卷积核内各点对应的权值.
① 确定坐标,假设为(0, 0);
② 把待求坐标,代入二维高斯滤波函数(式(5));
③ 计算出第二步的权值, �(0,0)=12�.
其它各点权值,可根据上面三步计算得出,归一化后,结果如图5所示:
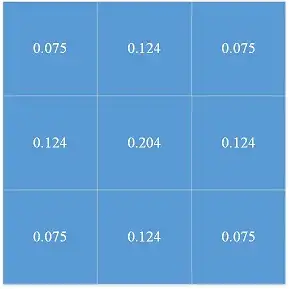
图5 各点权值
从图5所计算的权值可看出,高斯卷积核具备旋转对称性,表明对于边缘检测时,不会偏向任何方向. � 的值直接影响权值的分布, � 越大,中心点的权重越小,领域节点的权重越大,高斯平滑效果越好,但 � 过大,会导致图像丢失大量的细节信息;如果 � 过小起不到滤波的效果,不能达到有效去除噪声等目的,因此 � 的准确选择在实际问题的解决上存在重要的意义.
注:RGB三通道图像图像,高斯滤波是对每一个通道进行滤波处理,再重新合成RGB图像.- 双边滤波(Bilateral Filtering)
一般而言,图像边缘的有如下特征:
① 在图像的边缘部分,像素值的变化较为剧烈;
② 在图像的非边缘区域,像素值的变换较为平坦.
通过以上两点,我们可以总结出,若想保留图像边缘,在高斯滤波的基础上需引入一个能够衡量图像像素变换的剧烈程度的变量. 因此,我们引入了图像像素核 ��.
双边滤波的公式:(6)�pbf=1�pbf∑�∈����(||p−q||)���(|�p−�q|)�qwith �pbf=∑q∈����(||p−q||)���(|�p−�q|)
式(6)中, �q 为原图像中的某一像素; �pbf 为该点双边滤波后的像素值; ��� 为空间域核, ��� 为图像像素域核.
双边滤波中有两个衡量图像信息的重要变量,分别为 ��� 和 ��� . 空间域核就是我们上面讲的二维高斯函数,可把它视作高斯滤波,像素域核是衡量像素变化剧烈程度的量,将这两个量相乘,得到它们共同作用的处理效果:在图像的平坦区域,像素值变化幅度较小,每一个点对中心点的像素范围权重相近,此时,起主导作用的是空间域权重;在图像的边缘区域,像素值变化很大,边缘两侧的像素对中心点的像素范围权重相差较大,从而保持了边缘信息.
Q1:如何求解双边滤波后的图像呢?
A1:首先得知道两个计算公式:
① 空间域核计算方法:
(7)���(||�−�||)=exp(−(�−�)2+(�−�)22��2)
② 像素域核的计算方法:
(8)���(|��−��|)=exp(−[�(�,�)−�(�,�)]22��2)
式(7)中的 �� 和 �� 都是根据实际需求而人为设定. 而 �,�,�,� 都是需要我们像素在遍历中确定的值. 其中 (�,�) 代表窗口中心值,(m, n)代表的滑动窗口中的某一个像素值.
假定,有一张10×10的图像,如图6所示:滑动窗口大小为5×5.
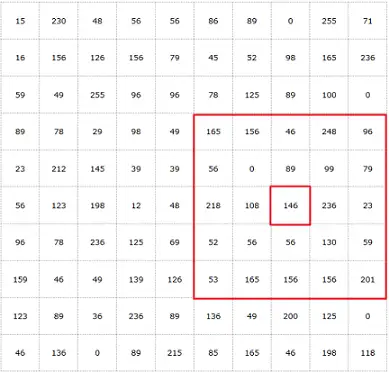
图6 双边滤波的原图像
Q2:如何求出中心点146的新像素值?
A2:
① 遍历整个窗口,第一个遍历的像素点是165,那么中心像素点146与该点的空间域结果为:
(9)���=exp(−(0−2)2+(0−2)22��2)
② 再计算中心点与该点的像素域结果:
(10)���=exp(−[146−165]22��2)
③ 当 �� =5, ��=20 时,由式(9)和式(10),分别可计算: ���=0.8521,���=0.6368 .
④ 遍历其它像素点,将窗口内每个像素点都与中心点建立联系,求出对应的 ��� 和 ��� 的值,将它们相乘,得到每个点对应的 �� ,即 ��=���×��� .
⑤ 遍历结束后,用每个点的 �� 乘上该点的像素值(m, n),并求和,作为分子;将每个点的 �� 相加,作为分母. 两者相除,即得到滤波后窗口中心点(i, j)的像素值.
参考:

 浙公网安备 33010602011771号
浙公网安备 33010602011771号