小黄鸡小组周赛 3 新手向题解
A - Takahashi san 2
翻译
KEYENCE 的文化是,无论角色、年龄或职位如何,都用后缀"-san "称呼每个人。
给你一个由小写英文字母组成的字符串 \(S\) 。
如果 \(S\) 以 "san "结尾,则打印 "是";否则打印 "否"。
思路
按照题目模拟就可以了。
代码
#include<bits/stdc++.h>
#define int long long
#define re register
using namespace std;
typedef pair<int,int> pii;
int n,m,k;
void solve() {
string s; cin >> s;
int len = s.size();
if(s[len-3] == 's' && s[len-2] == 'a' && s[len-1] == 'n') cout << "Yes\n";
else cout << "No\n";
return ;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
//int t; cin >> t; while(t--)solve();
solve();
return 0;
}
B - Unvarnished Report
翻译
KEYENCE 的文化是如实报告事情的好坏。
因此,我们想检查报告的内容是否与原文完全一致。
给你两个字符串 \(S\) 和 \(T\) ,由小写英文字母组成。
如果 \(S\) 和 \(T\) 相等,则打印 \(0\) ;否则,打印它们不同的第一个字符的位置。
在这里,如果 \(i\) /th字符只存在于 \(S\) 和 \(T\) 中的一个,则认为 \(i\) /th字符是不同的。
更确切地说,如果 \(S\) 和 \(T\) 不相等,打印满足以下条件之一的最小整数 \(i\) :
- \(1\leq i\leq |S|\) 、 \(1\leq i\leq |T|\) 和 $ i\neq T_i$ 。
- \(|S| \lt i \leq |T|\) .
- \(|T| \lt i \leq |S|\) .
这里, \(|S|\) 和 \(|T|\) 分别表示 \(S\) 和 \(T\) 的长度, \(S_i\) 和 \(T_i\) 分别表示 \(S\) 和 \(T\) 的 \(i\) 个字符。
思路
也没有什么思路,按照题目模拟就可以了。
需要注意的点是:
-
如果你用的是
string,它的下标从 \(0\) 开始,所以输出的时候答案要 \(+1\) -
\(S\) 和 \(T\) 相等要输出 0
代码
#include<bits/stdc++.h>
#define int long long
#define re register
using namespace std;
typedef pair<int,int> pii;
const int N = 1e6 + 10;
int n,m,k;
void solve() {
string s,t;
cin >> s >> t;
if(s == t) {
cout << 0 << "\n";
return ;
}
for(int i=0;i<min(s.size(),t.size());++i) {
if(s[i] != t[i]) {
cout << i + 1 << "\n";
return ;
}
}
cout << min(s.size(),t.size()) + 1 << "\n";
return ;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
//int t; cin >> t; while(t--)solve();
solve();
return 0;
}
C - Seats
翻译
一排有 \(N\) 个座位,编号为 \(1, 2, \ldots, N\) 。
座位的状态由长度为 \(N\) 的字符串 \(S\) 给出,该字符串由 "#"和". "组成。如果 \(S\) 的第 \(i\) 个字符是 "#",则表示座位 \(i\) 有人;如果是".",则表示座位 \(i\) 无人。
求在 \(1\) 和 \(N - 2\) 之间,满足以下条件的整数 \(i\) 的个数:
- 座位 \(i\) 和 \(i + 2\) 有人,座位 \(i + 1\) 无人。
思路
在 2 ~ n-1 范围内暴力枚举即可。(如果下标从 0 开始的是在 1 ~ n-2 枚举)
代码
#include<bits/stdc++.h>
#define int long long
#define re register
using namespace std;
typedef pair<int,int> pii;
const int N = 1e6 + 10;
int n,m,k,ans;
string s;
void solve() {
cin >> n >> s; ans = 0;
for(int i=1;i<s.size() - 1;++i) {
if(s[i] == '.' && s[i-1] == '#' && s[i+1] == '#') ans++;
}
cout << ans << "\n";
return ;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
//int t; cin >> t; while(t--)solve();
solve();
return 0;
}
D - Traveling Takahashi Problem
翻译
给你 \(n\) 个点,从 \((0,0)\) 开始按顺序直线走到其他点,最后再回到起点,求走过的路程。
思路
结合翻译和原题面给出的距离公式(欧几里得距离公式),就可以出思路了:设置两个变量 \(x,y\) 表示当前坐标,初始化为 \((0,0)\),每读入一个新坐标,就用公式计算两点的距离,最后更新坐标位置即可。
注意最后还需要回到原点,所以读取完新坐标后还需要额外计算当前坐标 \((x,y)\) 到 \((0,0)\) 的距离即可。
注意要保留小数。
代码
#include<bits/stdc++.h>
#define int long long
#define re register
using namespace std;
typedef pair<int,int> pii;
const int N = 1e6 + 10;
int n,m,k;
double p(double x) { // 计算平方的,pow写起来太难看
return x*x;
}
double add(double x,double y,double xx,double yy) { // 计算两点之间距离
return sqrt(p(xx-x) + p(yy-y));
}
void solve() {
cin >> n;
double ans = 0,x = 0,y = 0; // 初始化
for(int i=1;i<=n;++i) {
double xx,yy;
cin >> xx >> yy;
ans += add(x,y,xx,yy);
x = xx; y = yy; // 要记得更新坐标
}
ans += add(x,y,0,0); //要回到原点,所以还要算与原点的距离
cout << fixed << setprecision(10) << ans;
return ;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
//int t; cin >> t; while(t--)solve();
solve();
return 0;
}
E - Candy Button
翻译
有一个神秘的按钮。当你按下这个按钮时,你会得到一颗糖果,除非距离你上次得到糖果的时间少于 \(C\) 秒。
高桥决定按这个按钮 \(N\) 次。他将在 \(T_i\) 秒后按下 \(1\) 次这个按钮。
他会得到多少颗糖果?
思路
这题关键的数据是距离上次得到糖果的时间,那我们就用一个变量 las 记录上次拿到糖的时间,再和当前按下按钮的时间比较,如果大于等于 \(C\) 秒,那么就更新拿到糖的时间,同时累计答案。
注意它有可能会在第 \(0\) 秒按下按钮,因此我们要将(记录上次拿到糖的时间的变量) las 初始化为 \(-1\)。
代码
#include<bits/stdc++.h>
#define int long long
#define re register
using namespace std;
typedef pair<int,int> pii;
const int N = 1e6 + 10;
int n,m,k,c;
int ans;
void solve() {
cin >> n >> c;
int las = -1; //初始化
for(int i=1,x;i<=n;++i) {
cin >> x;
if(las == -1 || x-las >= c) { //如果是一开始(没有拿到糖,或者距离上次拿到糖的时间大于 C 秒)
ans++; las = x; //统计答案,更新拿糖时间
}
}
cout << ans << "\n";
return ;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
//int t; cin >> t; while(t--)solve();
solve();
return 0;
}
F - Hands on Ring (Easy)
翻译
给一些指令,每次指令都会选定左手或右手,你需要将被选定的这只手移动到指定位置,但是移动过程中不能碰到另一只手(移动路径上不能存在另一只手),问你操作的最小次数。
思路
一句话总结:讨论左右手和指定位置的相对关系即可。
很容易想到的是,手的移动方向只有两个,还被另外一只手卡住了一个。那就只能向另一边走了。哪个方向被卡住了呢?就需要讨论左右手和指定位置的关系。
代码
#include<bits/stdc++.h>
#define int long long
#define re register
using namespace std;
typedef pair<int,int> pii;
const int N = 1e6 + 10;
int n,m,k,c;
int ans;
void solve() {
cin >> n >> m;
int l = 1,r = 2;
for(int i=1,x;i<=m;++i) {
char c; cin >> c >> x;
if(c == 'L') {
if(r > x) {
if(l <= x || l < r) ans += abs(x-l);
else ans += x + n - l;
}
else if(r < x) {
if(l < r) ans += l + n - x;
else ans += abs(x - l);
}
l = x;
}
if(c == 'R') {
if(l > x) {
if(r <= x || r < l) ans += abs(x-r);
else ans += x + n - r;
}
else if(l < x) {
if(r < l) ans += r + n - x;
else ans += abs(x - r);
}
r = x;
}
}
cout << ans;
return ;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
//int t; cin >> t; while(t--)solve();
solve();
return 0;
}
G - Separated Lunch
翻译
由于 KEYENCE 总部的员工越来越多,他们决定将总部各部门分成两组,错开午休时间。
KEYENCE 总部有 \(N\) 个部门, \(i\) /-部门 \((1\leq i\leq N)\) 的人数为 \(K_i\) 。
将每个部门分配到 \(A\) 组或 \(B\) 组,让每个组在同一时间午休,并确保 \(A\) 组和 \(B\) 组的午休时间不重叠,求同一时间午休的最大人数的最小值。
换句话说,求分配给 \(A\) 组的部门总人数和分配给 \(B\) 组的部门总人数中较大者的最小值。
思路
我们将题目抽象出来:将数分为两个集合,集合的价值为他们所拥有的数之和,问这么多种分配方法中,两个集合较大着的最小值应该是多少。
因为数必须分为两个集合,所以一个数不是 \(A\) 集合就是 \(B\) 集合,那么我们只要知道 \(A\) 集合的价值,就知道了 \(B\) 集合的价值。我们很容易想到的方法是穷举法:穷举选 \(1\) 个人的最大价值最小是多少、穷举选 \(2\) 个人的最大价值最小是多少...,穷举选 \(n/2\) 个人的最大价值最小是多少。为什么到 \(n/2\) 就停止了呢?假设 \(n = 20\),我们选了 \(11\) 个人,那么另一个集合就选了 \(9\) 个,但是选 \(9\) 个这种情况我们已经枚举过了,所以就没必要再枚举了。
观察一下数据范围,\(n \le 20\),最坏时间复杂度是 \(O(2^{20})\)(粗略估计,实际比这个要小),可以使用穷举法。
穷举的方法有两种:\(dfs\) 和 状态压缩。由于猫猫太懒,下面先给出 dfs 做法,状态压缩的做法之后会更新。
代码
#include<bits/stdc++.h>
#define int long long
#define re register
using namespace std;
typedef pair<int,int> pii;
const int N = 1e6 + 10;
const int inf = 1e9 + 7;
int n,m,k,ans,sum;
int a[N],vis[N];
void dfs(int u,int tans,int lim) { // 当前搜索到的位置,当前所选的数之和,限制选几个。
if(lim == 0 || u > n) {
int num1 = tans;
int num2 = sum - tans;
ans = min(ans,max(num1,num2));
return ;
}
for(int i=u+1;i<=n;++i) {
if(!vis[i]) {
vis[i] = 1;
dfs(i,tans+a[i],lim-1);
vis[i] = 0;
}
}
}
void solve() {
cin >> n; ans = inf;
for(int i=1;i<=n;++i) {
cin >> a[i]; sum += a[i]; // 记得算所有数的总和,否则不知道另一集合的大小
}
sort(a+1,a+1+n); //也可以不排序,不影响。
for(int i=1;i<=n;++i) { //枚举限制选的个数,枚举到 n 和 枚举到 (n+1)/2 都没有影响。
dfs(0,0,i); //每次限制选的个数,再开始搜索
}
cout << ans << "\n";
return ;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
//int t; cin >> t; while(t--)solve();
solve();
return 0;
}
H - Spiral Rotation
翻译
给你一个有 \(N\) 行和 \(N\) 列的网格,其中 \(N\) 是偶数。让 \((i, j)\) 表示从上往下数第 \(i\) 行和从左往上数第 \(j\) 列的单元格。
每个单元格都涂成黑色或白色。如果 \(A_{i, j} =\) 则单元格 \((i, j)\) 为黑色;如果是 \(A_{i, j} =\) .,则为黑色。则为白色。
按以下顺序对 \(i = 1, 2, \ldots, \frac{N}{2}\) 进行操作后,找出每个单元格的颜色。
- 对于 \(i\) 和 \(N + 1 - i\) 之间的所有整数对 \(x, y\) ,用单元格 \((x, y)\) 的颜色替换单元格 \((y, N + 1 - x)\) 的颜色。同时对所有这些单元格对 \(x, y\) 进行替换。
思路
猫猫说不会写,其实是乱说的
之后这里会更新带图片的解释,如果看不懂文字,可以稍微等一会。
我们观察和研究一下替换的范围:所有坐标数字 \((x,y)\) 大小满足 \(i\) ~ \(n-i+1\) 的,都要替换。有点难理解?我们可以稍微模拟一下。
现在我有一个长度为 \(8\) 的矩阵。
- 起初,\(i = 1\),变化范围为 \(1\) 到 \(n - 1 + 1 = n = 8\),也就是红色区域。

- 然后,\(i = 2\),变化范围为 \(2\) 到 \(n - 2 + 1 = n - 1 = 7\),也就是绿色区域

- 接着,\(i = 3\),变化范围为 \(3\) 到 \(n - 3 + 1 = n - 2 = 6\),也就是蓝色区域
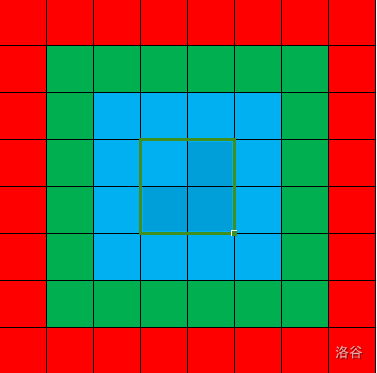
- 最后,\(i = 4\),变化范围为 \(4\) 到 \(n - 4 + 1 = n - 3 = 5\),也就是黄色区域

看完这里,相信你已经了解变化的范围了,接下来看替换规则:替换规则为 \((x,y)\) -> \((y,n-x+1)\)。在坐标轴上画一画,我们就可以发现这个的几何含义是顺时针旋转 90 度。
但是这题数据大小是 \(n \le 3000\),我们是没办法暴力修改每一个块的。我们再研究一下上面的图。可以发现,其实每个“圈”的旋转角度是固定的,例如,红圈每次只转 90 度,绿圈只转 180 度,篮圈只转 270 度,黄圈只转 360 度(相当于没转),再往下呢,又是一个新的循环。所以,每一圈赚多少我们是明确的。第一大外圈要转 90 度,第二大外圈要转 180 度,第三大外圈要转 270 度,第四大外圈不转...,以此类推。做法就出来了。
这题的另外一大难点是坐标的变换,这个需要自己去在草稿纸上模拟,也可以结合代码理解一下。
代码
#include<bits/stdc++.h>
#define int long long
#define re register
using namespace std;
typedef pair<int,int> pii;
const int N = 1e6 + 10;
const int inf = 1e9 + 7;
inline int read() {
int s=0,w=1; char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') {s=s*10+ch-'0';ch=getchar();}
return s*w;
}
int n,m,k,ans,sum;
char a[3010][3010],b[3010][3010];
void solve() {
cin >> n;
for(int i=1;i<=n;++i) {
for(int j=1;j<=n;++j) {
cin >> a[i][j];
}
}
int dir = 0; // 记录应该怎么转
for(int i=1;i<=n/2;i++) {
if(dir == 0) { // 顺时针旋转 90 度
for(int j=i;j<=n-i+1;++j) { //由于是同时修改,所以要先把修改后的状态放在另一个数组,才能实现同时修改
b[n-i+1][n-j+1] = a[j][n-i+1]; // right -> down
b[j][i] = a[n-i+1][j]; // down -> left
b[i][n-j+1] = a[j][i]; // left -> up
b[j][n-i+1] = a[i][j]; // up -> left
}
for(int j=i;j<=n-i+1;++j) { // 将状态修改回来。
a[i][j] = b[i][j];
a[n-i+1][j] = b[n-i+1][j];
a[j][i] = b[j][i];
a[j][n-i+1] = b[j][n-i+1];
}
}
if(dir == 1) {// 顺时针旋转 180 度
for(int j=i;j<=n-i+1;++j) {
b[n-i+1][n-j+1] = a[i][j]; // up -> down
b[i][n-j+1] = a[n-i+1][j]; //down -> up
b[n-j+1][i] = a[j][n-i+1]; //right - > left
b[n-j+1][n-i+1] = a[j][i]; //left -> right
}
for(int j=i;j<=n-i+1;++j) {
a[i][j] = b[i][j];
a[n-i+1][j] = b[n-i+1][j];
a[j][i] = b[j][i];
a[j][n-i+1] = b[j][n-i+1];
}
}
if(dir == 2) { // 顺时针旋转 270 度
//这里猫猫偷懒了,执行的是 旋转 90 度 + 旋转 180 度,虽然慢一点,但是也能达到相同的效果。
for(int j=i;j<=n-i+1;++j) {
b[n-i+1][n-j+1] = a[j][n-i+1];
b[j][i] = a[n-i+1][j];
b[i][n-j+1] = a[j][i];
b[j][n-i+1] = a[i][j];
}
for(int j=i;j<=n-i+1;++j) {
a[i][j] = b[i][j];
a[n-i+1][j] = b[n-i+1][j];
a[j][i] = b[j][i];
a[j][n-i+1] = b[j][n-i+1];
}
for(int j=i;j<=n-i+1;++j) {
b[n-i+1][n-j+1] = a[i][j];
b[i][n-j+1] = a[n-i+1][j];
b[n-j+1][i] = a[j][n-i+1];
b[n-j+1][n-i+1] = a[j][i];
}
for(int j=i;j<=n-i+1;++j) {
a[i][j] = b[i][j];
a[n-i+1][j] = b[n-i+1][j];
a[j][i] = b[j][i];
a[j][n-i+1] = b[j][n-i+1];
}
}
if(dir == 3) { // 旋转 360 度,等于没转。
}
dir = (dir + 1) % 4; // 重置旋转状态。
}
for(int i=1;i<=n;++i) {
for(int j=1;j<=n;++j) {
cout << a[i][j];
}
cout << "\n";
}
return ;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
//int t; cin >> t; while(t--)solve();
solve();
return 0;
}
I - Prepare Another Box
翻译
有 \(N\) 个玩具,编号从 \(1\) 到 \(N\) ;有 \(N-1\) 个盒子,编号从 \(1\) 到 \(N-1\) 。玩具 \(i\\ (1 \leq i \leq N)\) 的大小为 \(A_i\) ,盒子 \(i\\ (1 \leq i \leq N-1)\) 的大小为 \(B_i\) 。
高桥想把所有玩具分别存放在不同的盒子里,他决定按以下步骤依次进行:
- 选择一个任意正整数 \(x\) 并购买一个大小为 \(x\) 的盒子。
- 将每个 \(N\) 玩具放入 \(N\) 盒中(现有的 \(N-1\) 盒加上新买的盒子)。在这里,每个玩具只能放在一个大小不小于该玩具大小的盒子里,而且任何盒子都不能装两个或两个以上的玩具。
他想通过在步骤 \(1\) 中购买一个足够大的盒子来执行步骤 \(2\) ,但是大盒子的价格更高,所以他想购买尽可能小的盒子。
请判断是否存在一个值 \(x\) 使他可以执行步骤 \(2\) ,如果存在,求最小值 \(x\) 。
思路
形式化题意:加一个盒子使所有的玩具都能装下,或者说明不可能。
这题猫猫可能做复杂了,下面只讲猫猫自己的思路。当然如果你有更好的思路可以和猫猫说。
为了尽可能不让盒子浪费(大盒子装小玩具),每次我们都选择一个比玩具稍微大一点的盒子来装玩具,这个可以使用 multiset + 二分实现。同时我们需要使新加入的盒子大小最小,那么我们就对玩具从大到小排序,从最大的玩具开始选盒子(如果最大的玩具找不到盒子,那么比它小的玩具也找不到盒子)。如果出现选不到盒子的情况,我们就记录下这个玩具的大小,并跳过这个玩具。
无解的情况是:有两个及以上的玩具,在给定的盒子找不到能装的。由于我们只能添加一个盒子,所以所有玩具都装进盒子中是不可能实现的。
这里说明使用 multiset 的三点原因:盒子大小可能有重复;被选择过的箱子需要删除;箱子序列要保持有序才能二分。
代码
#include<bits/stdc++.h>
#define int long long
#define re register
using namespace std;
typedef pair<int,int> pii;
const int N = 1e6 + 10;
const int inf = 1e9 + 7;
int n,m,k,ans,sum;
int a[N];
multiset<int> s;
void solve() {
cin >> n;
for(int i=1;i<=n;++i) cin >> a[i];
for(int i=1,x;i<n;++i) cin >> x,s.insert(x);
sort(a+1,a+1+n);
for(int i=n;i>=1;--i) {
set<int>::iterator it = s.lower_bound(a[i]);
if(*it >= a[i]) { //能找到盒子
s.erase(s.lower_bound(a[i])); continue;
}
else {// 找不到盒子
if(ans == 0) { // 在此之前没有玩具装不下
ans = a[i];
}
else { // 在此之前已经有玩具装不下,只添加一个盒子是不可能的
cout << -1 << "\n"; return ; // 注意我直接 return 了,会直接回到主函数。
}
}
}
cout << ans << "\n";
return ;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
//int t; cin >> t; while(t--)solve();
solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号