Problems
在此记录刷过的题.
CF1895D 1900
注意到一旦我们确定了 \(b_0\)，那么整个 \(b\) 数组已经被唯一确定了。我们取 \(c_i\) 为 \(a_i\) 的异或前缀和，则 \(b_i=b_0\oplus c_i\)。
现在我们要将 \(b_i\) 全部降到 \(n\) 以下。那么我们可以对 \(c\) 建 trie 即可。
CF1992F 1900
考虑贪心，每次选尽量长的一段。现在问题来到如何判断是否应该分段。
首先若 \(a_i\) 不是 \(x\) 的约数，则 \(a_i\) 是没有贡献的，可以省略。
注意到 \(x\le 10^5\)，则 \(d(x)\) 最大只有 \(128\)。所以我们可以在执行过程中直接将元素能够构成的约数暴力塞进一个桶里判断即可。
不知道为何用 set 被卡了，改 vector 就过了。
CF1817B 1900
好水的 1900。
显然能成为鱼尾巴的那个节点连边条数要大于等于 \(4\)。所以直接对每个结点暴力 dfs 一遍然后找到最小的环即可。
CF1428D 1900
这个构造真的有蓝吗 /yiw
因为每个飞镖转一次之后是向右走的，所以从后往前考虑。
\(a_i=0\) 的位置直接忽略。
\(a_i=1\) 的位置直接新开一行。
\(a_i=2\) 的位置就接在一个 \(1\) 前面即可。
\(a_i=3\) 的位置可以选择一个行的末尾然后新开一行，优先选 \(2\), \(3\)。
CF1244G 2400
真的有 2400 吗？ Div3 真有你的。
首先上下界是很好构造的。
我们参考上界构造的方式，交换两个数的位置相当于增加 \(|i-j|\) 的贡献。
于是贪心构造即可。
mxoj 110122
若音符每个时刻只有一个，那么我们设 \(f_{i,j}\) 为一只手在 \(a_i\)，另一只在 \(j\) 上的最少体力。
那么有两个转移：
- 动第一只：\(f_{a_{i-1}, j} + dist(a_{i-1}, a_i) \to f_{a_i, j}\)
- 动第二只：\(\min_{j}(f_{a_{i-1}, j} + dist(j, a_i)) \to f_{a_i, a_{i-1}}\)
那么对于两个音符的情况，我们钦定后面的音符时第一个转移不进行，并且将不合法状态清空。
那么对于下面的第二个转移，将其中的 \(dist\) 拆开，分成四类讨论后上线段树优化。
mxoj 110127
\(n\le 10^5, m\le 50\).
trick：将连通块问题转化为平面图欧拉公式。
平面图欧拉公式: \(V-E+F=2\). （算上最外面那一个大面）
推论：联通块数量 \(C=V-E+F-1\).
将相邻的 \(1\) 之间连边，将他们看成整点，然后问题变为在网格图上面找有几个连通块。
直接 dfs 计算即可。
没看懂题解的更劣的分块做法。
AT_ttpc2015_o
trick：将判定性问题转化为计数问题。
考虑求出序列的 LIS 和 LDS 长度为 \(x,y\).
运气好的话，没有重复的数字。
若有重复的数字，那么最多只有一个。因为这是一个排列。
所以答案要么 \(x+y\) 要么 \(x+y-1\).
什么时候取不到 \(x+y\) 呢？
我们计算出每个位置 已经钦定被 LIS 与 LDS 同时选中 的方案数。
若是可能方案数与总方案数相同，则说明必定有重复的数。
计算可以用树状数组解决。
AT_joisc2019_d
很妙的扫描线题目。
我们钦定 \(i<j\).
对于位置 \(i\)，可行的位置为 \([i+l_i, i+r_i]\). 对于位置 \(j\)，可行的位置为 \([j-r_j, j-l_j]\).
那么我们对 \(i\) 的区间扫描线，分成插入 \(i\) 和删除 \(i\) 操作。
在进行到 \(j\) 的同时，将对应的区间打上一个 \(a_j\) 的 tag。
于是在线段树下传标记的时候，我们可以顺便计算 \(a_j-a_i\) 的最大值。
那么对于询问 \([L,R]\), 就是对应 \(i\in [L,R]\) 在 \(j=R\) 时的最大值。
至于由于标记未删除导致的额外贡献时不存在的。因为 \(i<L\) 的不会被算到，\(j<L\) 的不会将标记打到 \([L,R]\) 内。
注意在插入 \(i\) 的时候要将 \(i\) 的 tag 清空。
至于绝对值的话，将所有 \(a_i\) 取反再做一遍就可以了。
mxoj 110133
\(n\le 10^7\).
注意到最后返回值为 (seed ^ ans) & 0xffffff，于是 rnd() 的值域只有 0xffffff.
因为数据随机，所以我们可以认为数字在值域内均匀分布。
因为最小值会随机乱动，所以直接暴力模拟最小值的想法是错误的。
但是次小值不会。次小值只会单调递增，因为修改的只会是最小值。
所以暴力模拟次小值，实时维护最小值即可。
至于删除操作就打个懒标记就行了。
P3760
容易想到将贡献拆位。
对于每一位，分 4 类讨论它什么时候为 \(1\).
发现约束是关于后面几位的一个偏序关系。于是上树状数组就解决了。
P5443
神秘操作分块。
若没有修改操作，那么将询问离线，使用 Kruskal 重构树即可。
若 \(q\) 很小，那么有修改时直接修改后重构即可。
考虑将两者结合起来，对操作分块，将 不会被操作 的边直接拉出来，将询问离线。
在查询的时候，将 会被操作 的边暴力操作，再重新塞回重构树中。
查询完毕将塞入的边再重新取出来继续做。需要用到可撤销并查集。
复杂度 \(O(q\sqrt m\log m)\)，但是跑的很快。
P3203
来做经典题啦。
考虑对序列分块，每个位置维护两个信息：
-
要跳几次才能跳出这个块。
-
跳出这个块后会跳到哪个位置。
于是查询按块查询，修改暴力重构即可。
时间复杂度 \(O(q(\frac nB+B)) \ge O(q\sqrt n)\).
mx130007
题意：
强制在线维护两种操作：
-
向树中挂一个叶子。
-
查询某个点子树大小。
\(n\le 8\times 10^5\)
考虑和弹飞绵羊一样的分块做法，将序列分块，维护每个节点跳出这个块时跳到哪个节点。
然后挂叶子的时候跳块处理，查询的时候暴力将块内贡献重新计算一遍即可。
时间复杂度 \(O(q(\frac nB+B)) \ge O(q\sqrt n)\).
mx130012
题意：求树上前 \(k\) 大菊花的权值和，点有点权，可正可负，大小必须大于等于 \(3\)。
\(n, k\le 3\cdot 10^5\)
Codeforces 上有类似做法原题，I. Show Must Go On
首先将所有权值排序，然后考虑怎么从一个最大值生成新的最大值。
我们考虑我们选定了大小为 \(m\) 的子集。
首先一定是选前 \(m\) 个最优。之后每次可以将最后一个没有固定的位置向后挪动一格，或者固定一个位置。
注意在挪动的时候要保证位置的相对顺序。也就是不能跨越。
证明很简单：当 \(i\) 要跨越 \(i+1\) 的时候，不如将 \(i+1\) 向后挪一挪。
设状态 \((k,u,v)\) 代表有 \(k\) 个没动过，当前动的这个在 \(u\) 位置，下一个固定位置在 \(v\)。
所以合法状态 \((k,u,v)\) 可以转移到 \((k,u+1,v)\) 和 \((k-1,k+1,u)\)。
注意不合法状态是不能存在的，即 \(u<v\) 的时候状态才存在。
随后我们将所有状态塞进优先队列中，每次取最大的出来，随后扩展状态即可。
状态总数是 \(O(k)\) 的。所以总复杂度 \(O(k\log k)\)。
qoj 4738
首先有一个次数为 \(\frac{n^2}{4}+O(n)\) 的做法。
考虑如何确定一个位置。
暴力的想法是：直接将第一个与每一个地方都询问一次。
若答案 +2 则皆大欢喜，答案 +1 时则必定有两个位置是 +1。
那么就会涉及到 \(3\) 个位置，随便换一下就可以得出 \(2\) 个位置的数。
但是这个做法需要整个序列是错排的，随机一个即可。
但是过不了。
发现排列错排之后，关键在于如何找出一个能使答案增加的位置，而与方案是无关的。
所以考虑直接将所有没确定的位置单独拎出来，两两随机匹配并且交换。
若答案没有增加就再随机匹配一次。
随后我们可以二分出第一个使答案增加的交换对是哪一对。
那么我们就确定了一个对 \((i,j)\)，使得交换之后 至少一个是对的。
那我们就在原来的序列上什么都不做，只交换 \((i,j)\) 并询问。
若答案 +2 则皆大欢喜，答案 +1 时分类讨论，有下表：
选择一个位置 k，优先选已经确定的。
位置：(k, i, j) 0/1 : 位置当前是否正确。
考虑直接交换 (k,i).
(1, 1, 0) -> (0, 0, 0) Ans-2; (1, 0, 1) -> (0, 0, 1) Ans-1 (有对的)
(0, 1, 0) -> (0, 0, 0) Ans-1; (0, 0, 1) -> (0, ?, 1) Ans+? (没对的)
那么就可以用多 \(1\) 次操作确定一个位置。
总操作数 \(n\log n+O(n)\)，实则当 \(n=256\) 时次数是 \((9+\epsilon)n\)，可以通过。
mxoj130020 / CFgym104976E
Trick：前面操作有后效性，后面操作无前效性时，考虑 时光倒流 / 从后往前考虑。
后面的字符串对于前面来说的限制是：限制某个长度的前缀的字符集是什么。
那么考虑从后往前加入每一个字符串，对于限制来说，是很好转移的。
插入之后，再添加一个限制是长度为 \(|s_i|\) 的前缀的字符集是 \(s_i\).
于是可以得到一个 \(O(n^2)\) 的解法。
但是当有同一个前缀有多个限制时：随便保留一个限制即可，最后生成完字符串之后再判断是否合法即可。
总复杂度：\(O(\min(n^2,\sum l))\).
mxoj130015
我吃棒棒糖。
赛时一直在想二分答案，判断的时候再 dp，然后只有 \(O(n\log^2n)\) 的解法。
但是直接贪心即可。贪心选最大的那一对数，然后将大的那个删掉。
正确性：若不删最大的，则答案不会下降。如果要删最大的那一对，则删小的一定不优。
直接模拟即可。复杂度 \(O(n\log n)\).
mxoj130016
\(n\le 300\).
因为需要满足 \(k_i>i\) 所以考虑从后往前加入点，条件就自动满足了。
现在对于儿子数量分类讨论。
(1) 没儿子：选择 一个可以填的地方填上 或者 新开一个树。
(2) 一个儿子：选择 一个可以填的地方填上 或者 新开一个树。
(3) 两个儿子：选择 一个可以填的地方填上 或者 新开一个树 或者 连在某个树头上 或者 合并两个树。
那么设状态 \(f_{i,j,k}\) 是填了 \(i\) 个点，有 \(j\) 颗树，有 \(k\) 个儿子位置可以填，转移如下面所示。
if(l[i]<=0&&0<=r[i])
{
(f[bit][j+1][k]+=f[bit^1][j][k])%=mod; // as new tree
if(k) (f[bit][j][k-1]+=k*f[bit^1][j][k])%=mod; // as a son
}
if(l[i]<=1&&1<=r[i])
{
(f[bit][j+1][k+1]+=2*f[bit^1][j][k])%=mod; // as new tree
(f[bit][j][k]+=2*k*f[bit^1][j][k])%=mod; // as a son
}
if(l[i]<=2&&2<=r[i])
{
(f[bit][j+1][k+2]+=f[bit^1][j][k])%=mod; // as new tree
(f[bit][j][k+1]+=k*f[bit^1][j][k])%=mod; // as a son
(f[bit][j][k+1]+=2*j*f[bit^1][j][k])%=mod; // pick a tree
if(j>1) (f[bit][j-1][k]+=2*k*(j-1)*f[bit^1][j][k])%=mod; // merge 2 trees
}
mx130043
题意：给定 \(n\cdot m\) 个由小写字母组成的字符串 \(s_{i,j}\).
求：\(\sum_{i=1}^n\sum_{j=1}^n\max_{k=1}^m\operatorname{LCP}(s_{i,k},s_{j,k}).\) 其中 \(\operatorname{LCP}\) 是最长公共前缀函数。
Trick: 看到 \(\max\) 的式子，而 \(\max\) 不好求，\(\min\) 好求的话，采用 minimax 容斥。
minimax 容斥：
那么我们的式子变成了这样：令 \(S=\{1,2,...,m\}\).
则答案为：
\(\begin{aligned}
\sum_{i=1}^n\sum_{j=1}^n\sum_{T\subset S}(-1)^{|T|+1}\min_{k\in T}\operatorname{LCP}(s_{i,k},s_{j,k})\\
=\sum_{T\subset S}(-1)^{|T|+1}\sum_{i=1}^n\sum_{j=1}^n\min_{k\in T}\operatorname{LCP}(s_{i,k},s_{j,k})
\end{aligned}\)
发现 \(\min\) 明显相对更加好求。
要使 \(\min\) 增加，则所有相应的位置都应该相同。
那么我们在求集合 \(T\) 的答案的时候，可以参考部分分中 \(|S|=1\) 的做法：
将多个串合并成一个串，然后放进 Trie 中计算答案。
如何合并？按每一位将他们串起来。例如：aab 和 baa 和 cba，串完后变成 abcaabbaa。
那么统计答案的时候就不能在任意一个节点都计算答案了。只有在深度是 \(|T|\) 的倍数的时候才能统计答案。
最后按上面的式子统计一下答案即可。
qoj 5039
发现关系就很好做了。
考虑最朴素的情况：直接向上走 \(n\) 步再一直向右走。
那么显然这样的路径答案为 \(0\).
每次我们想要添加一个格子，那么肯定是这样：
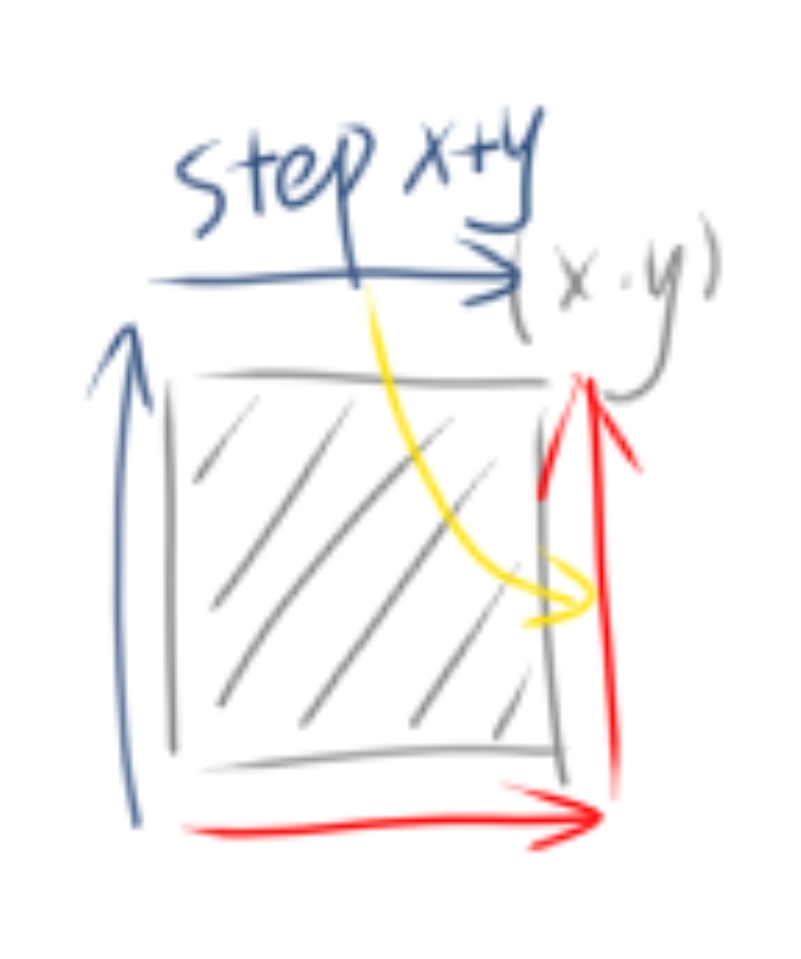
第 \(x+y\) 步和格子 \((x, y)\) 的颜色启示我们考虑两者之间的联系。
所以有以下结论：
考虑所有奇数步，若从向右改为向上，则答案 \(-1\)，若从向上改为向右，则答案 \(+1\)。
那么可以非常快速的算出 奇数步中有多少步向上，偶数步中有多少步向上。答案就是两个组合数之积，即：
qoj 14945
若两个人在同一个点，显然无解。
若两个人不相邻，显然肯定有解。构造就直接让两人定在原地即可。
若两个人相邻，一个人肯定可以追着另一个人跑。所以若某一方停下，则游戏必然失败。
所以最终肯定是在一个环上跑。
对于环，还必须是极小环。否则肯定一方可以走环上的弦而领先另一方从而游戏结束。
所以只需要找到两人最近的极小环然后一路跑过去即可。
对于其他边，让他们过不去即可。
qoj 11802
奇异搞笑题。
我们直接考虑 \((x, y)\) 这条边，令 \(X\) 为两点黑边条数的随机变量。
若无，则协方差为 \(0\)。若有，则协方差为 \(\frac 14\)。
所以直接算就好了。\(30s\) 时限是何意味。
qoj 10426
构造。
显然整棵树的 理论最大值 直接贪心自底向上选择边即可求得。
我们考虑构造这个理论最大值，查看是否能行。
记 \(cnt_x\) 的值为 \(x\) 颜色在出现在答案边端点上的次数。
那么会出现 \(3\) 类边：
一类边：\(cnt_{a_u}=1,cnt_{a_v}=1\)
二类边：\(cnt_{a_u}=1,cnt_{a_v}=2\)
三类边：\(cnt_{a_u}=2,cnt_{a_v}=2\)
对于一类边，设有边和点 \((a,b),a',b'\). 直接执行 \(<a',b>\) 即可。
剩下的边只有两种情况：
第一种，只有三类边。
设有边和点 \((a,b),(b',c),(c',d),(d',a')\).
将除最后一个点按顺序列出来：\([a, b, b', c, c', d, d']\)
一头一尾交换即可。
即：\(<a, d'>, <b, d>, <b', c'>\).
第二种，二类边夹着三类边。
设有边和点 \((a,b),(b',c),(c',d),(d',e),a',e'\).
发现执行 \(<e,a'>\) 后就相当于第一种情况了。
即：\(<e, a'>, <a, d'>, <b, d>, <b', c'>\).
然后就解决了。
???
题意：多测，每次给出长度为 \(m\) 的数组 \(a\) 和 \(k\)，求以下式子的值：
\(T \le 10, m \le 25, k \le 60\).
赛场不会含泪拿下 60pts，算是废了。
Key observation 1: \(\operatorname{parity}(x)=\Large\frac{1-(-1)^{\operatorname{popcount}(x)}}{2}\).
所以原式变为：
枚举集合 \(S\) 作为选择 \(-1\) 这项的下标，则变为：
Key observation 2: \((-1)^{\operatorname{popcount}(x\&(a\oplus b))}=(-1)^{\operatorname{popcount}(x\&a)}\cdot (-1)^{\operatorname{popcount}(x\&b)}\).
所以原式变为：
拆位考虑，令 \(v=\oplus_{i\in S}a_i\)，\(v_p\) 为 \(v\) 二进制下的第 \(p\) 位。
若 \(v_p=0\)，则对和的贡献是乘上 \((1+3^{2^p})\)。
若 \(v_p=1\)，则对和的贡献是乘上 \((1-3^{2^p})\)。
分块预处理，设阈值为 \(B\)，预处理出 \(2^B-1\) 以内所有 \(v\) 的结果，最后对于总的 \(v\) 再将他们合并即可。
时间复杂度 \(O\left(\frac kB2^B+T\cdot 2^m\right)\).
浙公网安备 33010602011771号