完全二叉树判断,简单而复杂
今天有个人问我如何判断一棵树是完全二叉树。我一下子想不出怎么解决这个问题,按照定义,
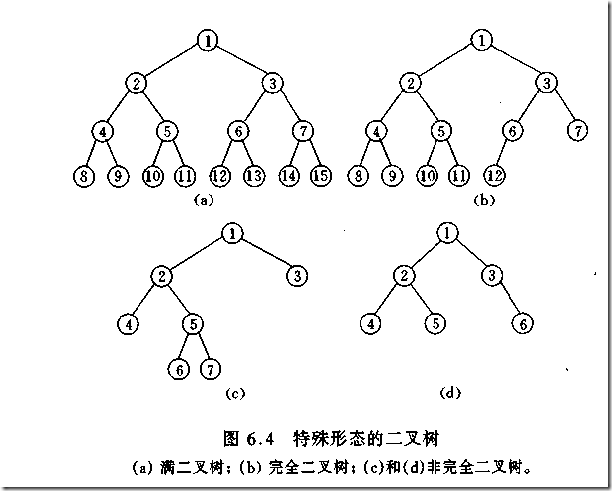
严蔚敏那本教材上的说法:一个深度为k,节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解,
就是一棵树,深度为k,并且没有空位。
首先对满二叉树按照广度优先遍历(从左到右)的顺序进行编号。
一颗深度为k二叉树,有n个节点,然后,也对这棵树进行编号,如果所有的编号都和满二叉树对应,那么这棵树是完全二叉树。
概念我基本上能明白,但是,如何判断我居然写不出来。哎,这样简单的数据结构题,居然不会。
于是我google 了好一阵子,找了十几个算法,解决方案基本上是判断,有右子树,就不能有左子树,等等。基本上是反证法,找反例,由于,可能性有很多,仔细以推敲这些算法都有漏洞。这让我想起必须从不同的角度来思考这个问题。
任意的一个二叉树,都可以补成一个满二叉树。这样中间就会有很多空洞。在广度优先遍历的时候,如果是满二叉树,或者完全二叉树,这些空洞是在广度优先的遍历的末尾,所以,但我们遍历到空洞的时候,整个二叉树就已经遍历完成了。而如果,是非完全二叉树,
我们遍历到空洞的时候,就会发现,空洞后面还有没有遍历到的值。这样,只要根据是否遍历到空洞,整个树的遍历是否结束来判断是否是完全的二叉树。
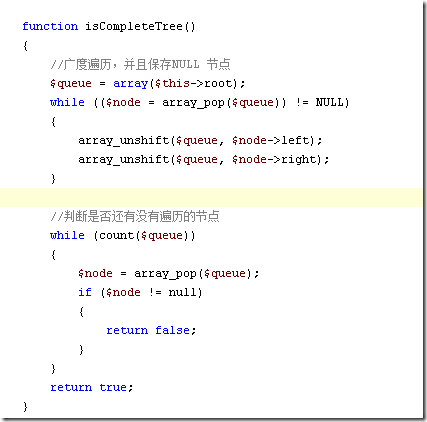
这样代码就非常的简单了:
代码是PHP代码,只拷贝了核心的部分。$this->root 保存了树的根。
这个判断方法,暂时没有找到什么漏洞,欢迎博客园的朋友们给我一个更加好的解决方案。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号