2.1 基本统计量与数据可视化
1.均值、中位数、分位数、三均值
均值、中位数:mean(A)、media(A)
分位数:prctile(A,P),P∈[0,100]
prctile(A,[25,50,75]) %求A的下、中、上分位数
三均值:
w=[0.25,0.5,0.75];
SM=w*prctile(A,[25,50,75])
%例:计算安徽16省市森林资源统计量
A=xlsread('senlin.xls','sheet1')
M=mean(A); %均值,
MD=median(A); %中位数
SM=[0.25,0.5,0.25]*prctile(A,[25,50,75]); %三均值
[M;MD;SM]
2.方差、标准误、变异系数
方差:var(A,flag),flag默认0表示修正的方差,取1为未修正
标准差:std(A,flag),同上
变异系数:v=std(A)./abs(mean(A))
k阶原点矩、中心距:
ak=mean(A.^k)
bk=mean((A-mean(A)).^k)
%中心距系统命令bk=moment(A,k)
3.极差、四分位极差(上、下分位数之差)
R=rangr(A)
R1=iqr(A)
4.异常点判别(截断点)
XJ=parctile(A,[25])-1.5*R1
SJ=parctile(A,[75])+1.5*R1
5.偏度、峰度
偏度:sk=skewness(A,flag),默认1,取0为样本数据修正的偏度
峰度:ku=kurtosis(A,flg)-3,同上
2.1.2 多维样本数据
协方差:cov(A)
相关系数:corr(A)
标准化:zscore(A)
2.1.3 样本数据可视化
1.条形图
bar(x)%样本数据x的条形图,横坐标为1:length(x)
bar(x,y)%先把x和y一一对应,然后将x从小到大排序画图
2.直方图
hist(x,n)%数据x的直方图,n为组数,确省时n=10
[h,stats]=cdfplot(x)%x的经验分布函数图,stats给出数据最大最小值、中位数、均值、标准差
直方图基础上附加正态密度曲线
histfit(x)
histfit(x,nbins)%nbins指定bar个数,缺省时为x中数据个数的平方根
3.盒图,五个数值点组成:最小值、下四分位数、中位数、上四分位数、最大值。中间的盒子从Q1延申到Q3,盒子的直线标出中位数位置,盒子两端有直线往外延伸到最小数与最大数
boxplot(x)%矩阵x的每一列的盒图和“须”图,
4.阶梯图
stairs(x)%x的阶梯图
5.火柴棒图
stem(x)%离散数据的火柴棒图
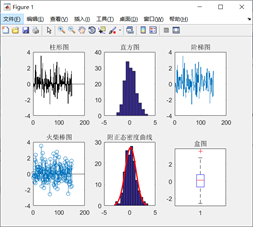
%例:随机150个服从标准正态分布随机数,做出柱形图、直方图、阶梯图、火柴棒图
x = random('normal',0,1,[1,150]); %产生服从标准正态分布随机数150个
subplot(2,3,1),bar(x),title('柱形图')
subplot(2,3,2),hist(x),title('直方图')
subplot(2,3,3),stairs(x),title('阶梯图')
subplot(2,3,4),stem(x),title('火柴棒图')
subplot(2,3,5),histfit(x),title('附正态密度曲线')
subplot(2,3,6),boxplot(x),title('盒图')
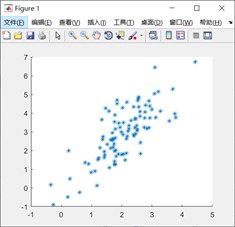
例:(X,Y)服从二维正态分布N(2,1;3,3;sqrt(3)/2),生成100对数据做出三点图画出二维正态分布的密度函数,绘制密度曲面图形
mu = [2 3]; %输入均值向量
sa = [1 1.5; 1.5 3]; %输入协方差矩阵
Nr = mvnrnd(mu,sa,100); %随机生成n=100的样本数据
scatter(Nr(:,1),Nr(:,2),'*'); %作样本数据平面散点图
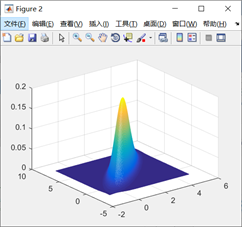
%绘制密度曲面
figure(2)
v=sqrt(3)/2; %输入相关系数
x=-1:0.05:5; %横坐标的取值向量
y=-2:0.05:8; %纵坐标的取值向量
[X,Y]=meshgrid(x,y); %生成网格点
T=((X-mu(1)).^2/sa(1,1)-2*v/sqrt(sa(1,1)*sa(2,2))*(X-mu(1)).*(Y-mu(2))+(Y-mu(2)).^2/sa(2,2));
Z=1/(2*pi)/sqrt(det(sa))*exp(-1/2/(1-3/4)*T); %计算密度函数值
mesh(X,Y,Z) %绘制密度曲面图形

3.正态概率图和Q-Q图
(1)正态概率图:normplot(x)%样本数据对应图中的+,若+大都集中在红色参考线上则说明服从正态分布
若总体是非正态分布,可以类似绘制概率图(威布尔分布概率图)
weibplot(x)%若样本数据点基本散布在一条直线上,则数据服从该分布
(2)Q-Q图:
PD=fitdist(x,distname)%distname为Beta、Binomial、Exponential、Normal、Weibull
qqplot(x,PD)% PD省略时为标准正态分布
%例:自由度为8的卡方分布数据300个,绘制其正态概率图与卡方分布的Q-Q图
clear
s=rng;rng(s);
c1=chi2rnd(8,[300,1]); c2=sort(c1); %模拟生成卡方分布样本
plot(c2,chi2pdf(c2,8), '+-'); %绘制卡方分布的密度曲线
title('卡方分布的密度曲线') ;legend('自由度n=8');
grid on %打开网格
figure
pd=makedist('Gamma','a',4,'b',0.5) %创建参数a=4,b=0.5的伽马分布
%pd=gamrnd(4,0.5,[300,1]);
subplot(1,2,1),normplot(c1); %绘制样本的正态概率图
subplot(1,2,2),qqplot(c1,pd); %按指定分布绘制样本的Q-Q图
grid on
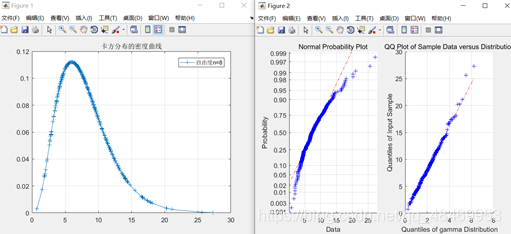
左图可看出是左偏,中图偏离参考线故不服从正态分布,右图贴合直线故服从伽马分布(自由度为8的卡方分布就是参数a=n/2,b=0.5的伽马分布)
2.2 数据分布及其检验
1.经验分布函数
[h,stats]=cdfplot(x)%x的经验分布函数图,h表示曲线的环柄,stats给出数据最大值、最小值、中位数、均值、标准差
%例:生成服从标准正态分布的50个样本点,画出样本的经验分布函数图,并与理论分布函数比较
clear
X=normrnd (0,1,50,1); %生成服从标准正态分布的50行1列样本点
[h,stats]=cdfplot(X); %样本的经验分布函数图
hold on %保持上图,后续图层叠加在上图
plot(-3:0.01:3, normcdf(-3:0.01:3,0,1), 'r') %理论分布函数图
legend('样本经验分布函数Fn(x)', '理论分布函数Φ(x)','Location','NorthWest')

2.总体分布正态性检验
(1)JB检验:显著性水平alpha默认0.05
%以下两种方法均可,输出的H=0无法拒绝X服从正态分布;H=1拒绝。P为接受假设的概率值,P<alpha,则拒绝正态分布原假设。JBSTAT为测试统计量,CV是拒绝临界值,JBSTAT>CV拒绝。
H=jbtest(x,alpha)
[H,PJBSTAT,CV]=jbtest(x,alpha)
(2)KS检验:
h=kstest(x)
h= kstest(x,cdf)
[h,p,ksstat,cv]=kstest(x,cdf,alpha)
%h=0无法拒绝X服从正态分布
(3)Lilliefors检验(改进的KS检验):
H=lillietest(x,alpha)
[H,P,LSTAT,CV]=lillietest(x,alpha)
%判断方法同(1)
%例:检验“中国银行”的股票的收盘价是否服从正态分布。
clear
a=xlsread('yhgspj.xls'); %读取收盘价数据
h1=jbtest(a(:,1)) %JB检验
h2=kstest(a(:,1)) %KS检验
h3=lillietest(a(:,1)) %改进KS检验
qqplot(a(:,1))
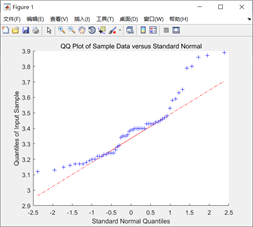
h1=1,h2=1,h3=1,三种检验均拒绝正态分布原假设,Q-Q图显示偏离参考线,不服从正态分布
2.2.2 多维数据的正态分布检验
%例:三组数据有4项指标,三组视为一个总体,是否服从四维正态分布
clear
A=xlsread('jibing.xls','sheet1')
X=[A(:,1:4);A(:,5:8);A(:,9:12)];
[N,p]=size(X);
d=mahal(X,X); % 计算马氏距离
d1=sort(d); % 从小到大排序
pt=[[1:N]-0.5]/N; % 计算分位数
x2=chi2inv(pt,p); % 计算X2t
plot(d1,x2','*',[0:12],[0:12],'-r') % 作图
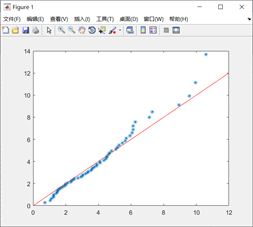
数据点基本落在直线上,不能拒绝正态分布原假设
3.多个总体协方差矩阵相等性检验
(1)两总体
%例:蠓虫分类
clear
apf=[1.14,1.78; 1.18,1.96;1.20,1.86;1.26,2.;1.28,2;1.30,1.96];
af=[1.24,1.72;1.36,1.74;1.38,1.64;1.38,1.82;1.38,1.90;1.40,1.70;1.48,1.82;1.54,1.82;1.56,2.08];
n1=6;n2=9;p=2;
s1=cov(apf);s2=cov(af);
s=((n1-1)*s1+(n2-1)*s2)/(n1+n2-2); % 计算混合样本方差
Q1=(n1-1)*(log(det(s))-log(det(s1))-p+trace(inv(s)*s1));
Q2=(n2-1)*(log(det(s))-log(det(s2))-p+trace(inv(s)*s2));% 计算检验统计量观测值
ch2inv(0.95,3) %计算X2(3)临界值
Q1=2.5784<7.8145,Q2=0.7418<7.8145,无法拒绝两类总体协差阵相同的原假设
(2)多总体
%例:上上个例子三组数据的协方差矩阵是否相等?...
clear,clc
A=xlsread('jibing.xls','sheet1'); %输入样本数据
G1=A(:,1:4); %提取总体1的样本
G2=A(:,5:8);
G3=A(:,9:12);
n=size(G1,1)+ size(G2,1)+ size(G2,1); %计算总的样本容量
[n1,p]= size(G1);
k=3;
f=p*(p+1)*(k-1)/2; %统计量自由度
d=(2*p^2+3*p-1)*(k+1)/(6*(p+1)*(n-k));
s1=cov(G1); %协方差矩阵
s2=cov(G2); %协方差矩阵
s3=cov(G3); %协方差矩阵
s=(n1-1)*(s1+s2+s3)/(n-k); %总体协方差估计
M=(n-k)*log(det(s))-19*(log(det(s1))+log(det(s2))+log(det(s3)));
T=(1-d)*M
P0=1-chi2cdf(T,f) % 卡方分布概率
P=0.4374>0.1故无法拒绝三个总体协方差矩阵相等的原假设
本文用到的三个excel文件如下
链接:https://pan.baidu.com/s/1oKCsLTsU99CjQciIKmPRKw
提取码:nj03
内容来源于吴礼斌和李柏年老师主编的《MATLAB数据分析方法》,包括但不限于课本内容,记载学习记录以及自身见解,侵权联系删除。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号