夜的独白

  博客园  :: 首页  :: 新随笔  :: 联系 :: 订阅 订阅  :: 管理
（五）【Matlab】数据分析与多项式计算A 数据统计分析B 多项式计算C 数据插值(interp)D 曲线拟合(plotfit)

【Matlab】

文章目录

  • A 数据统计分析
  • * A.a 求最大值与最小元素
    • A.b 求平均值和中值
    • A.c 求和与求积
    • A.d 累加和与累乘积
    • A.e 求标准差与相关系数
    • A.f 排序
  • B 多项式计算
  • * B.a 多项式的表示
    • B.b 多项式的四则运算
    • B.c 多项式的求导(polyder)
    • B.d 多项式积分(polyder)
    • B.e 多项式的求值(polyval;polyvalm)
    • B.f 多项式的求根(roots;poly)
  • C 数据插值(interp)
  • * C.a 引例-零件加工问题
    • C.b 数据插值的计算机制
    • C.c 数据插值的实现方法
  • D 曲线拟合(plotfit)
  • * D.a 引例-人口预测问题
    • D.b 曲线拟合的原理
    • D.c 曲线拟合的实现方法

A 数据统计分析

A.a 求最大值与最小元素

在这里插入图片描述
![在这里插入图片描述](https://img-blog.csdnimg.cn/2020022718580247.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
例子：
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227190011812.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227190312603.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
（3）中的[]不可省略
![在这里插入图片描述](https://img-blog.csdnimg.cn/2020022719141987.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
例子：
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227191501205.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227191515539.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227191641383.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

A.b 求平均值和中值

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227191748542.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

    mean()      % 求算术平均值
    median（）  % 求中值

A.c 求和与求积

    sum()    % 求和
    prod（） % 求积

A.d 累加和与累乘积

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227192228863.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

A.e 求标准差与相关系数

在这里插入图片描述
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227193539276.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

在这里插入图片描述
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227220247271.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

A.f 排序

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227220407767.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
例子：
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227220633972.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)

B 多项式计算

B.a 多项式的表示

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227221538611.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

B.b 多项式的四则运算

在这里插入图片描述
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227221730390.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
例子： ![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227221951225.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)

B.c 多项式的求导(polyder)

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227222057467.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
例子：
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227223129310.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
在这里插入图片描述

B.d 多项式积分(polyder)

q = polyint(p,k) 使用积分常量 k 返回 p 中系数所表示的多项式积分。
示例：计算定积分
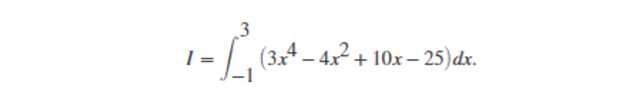
在这里插入图片描述

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200527131352629.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

B.e 多项式的求值(polyval;polyvalm)

在这里插入图片描述

在这里插入图片描述
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227224021103.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)
在这里插入图片描述

B.f 多项式的求根(roots;poly)

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227224328846.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227224352731.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227224439105.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

C 数据插值(interp)

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227224913999.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

C.a 引例-零件加工问题

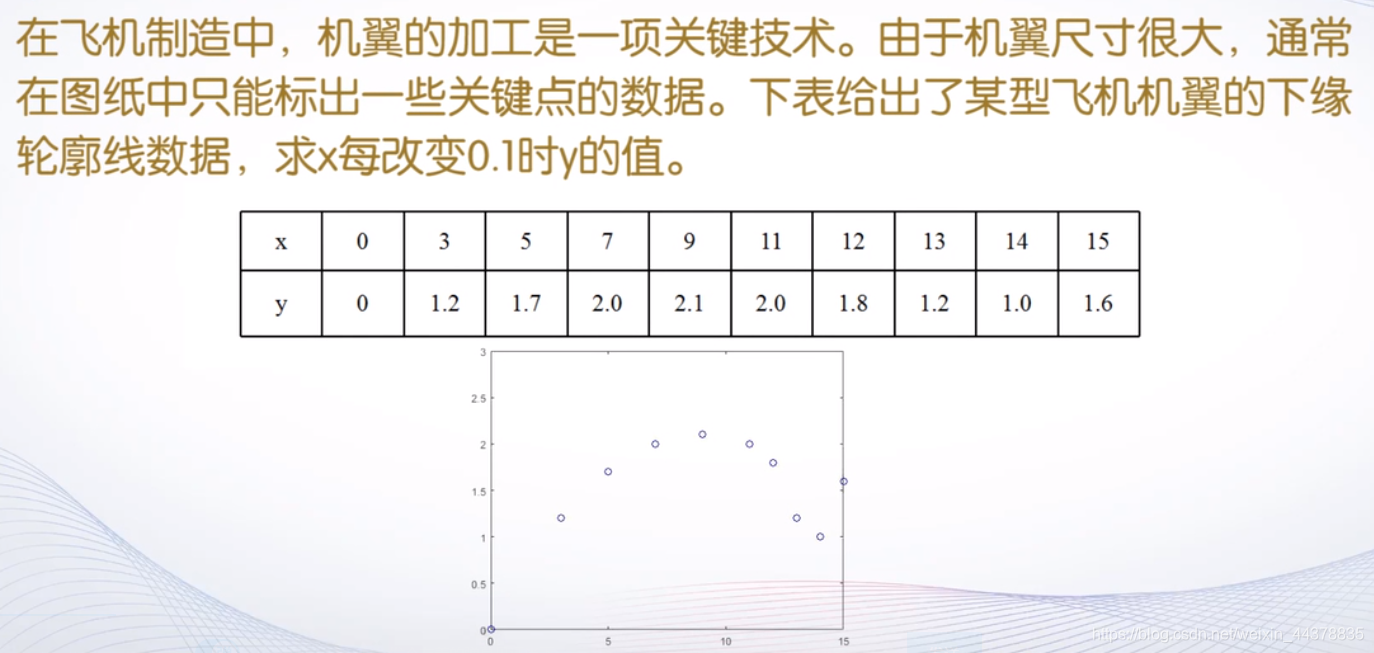
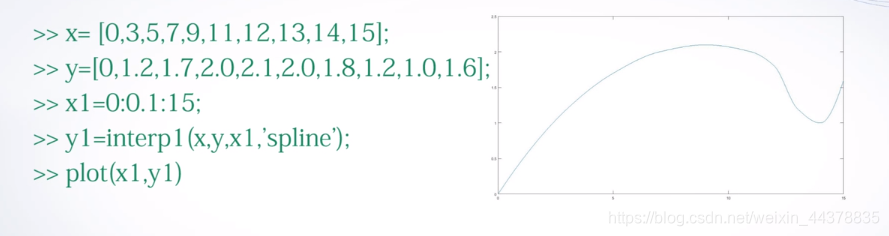
![在这里插入图片描述](https://img-blog.csdnimg.cn/2020022722541148.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227225449602.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)

C.b 数据插值的计算机制

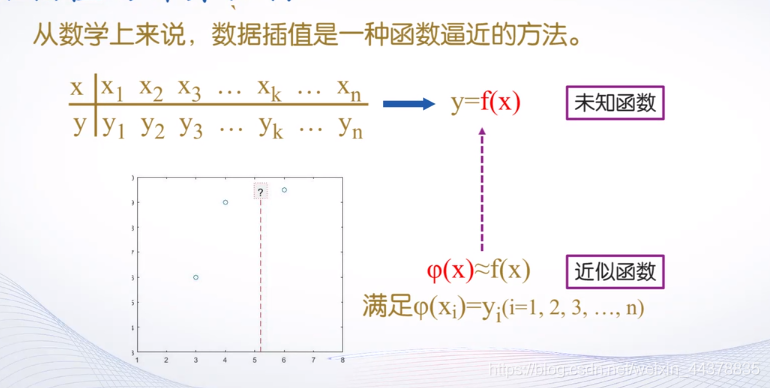
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227225630677.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227225837710.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)

C.c 数据插值的实现方法

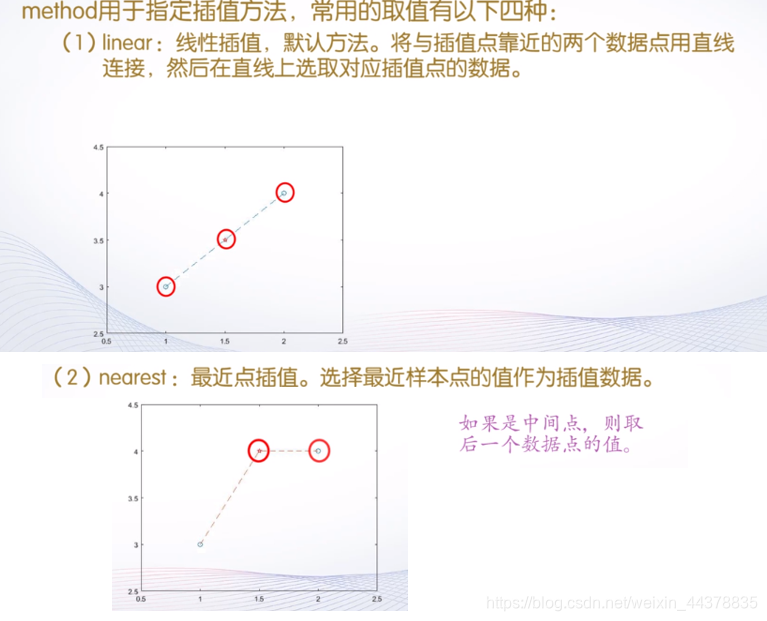
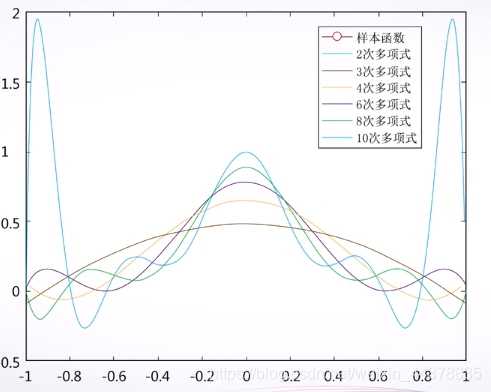
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227230110162.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227230200762.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
在这里插入图片描述
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227230323972.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
引例用四种方法插值：
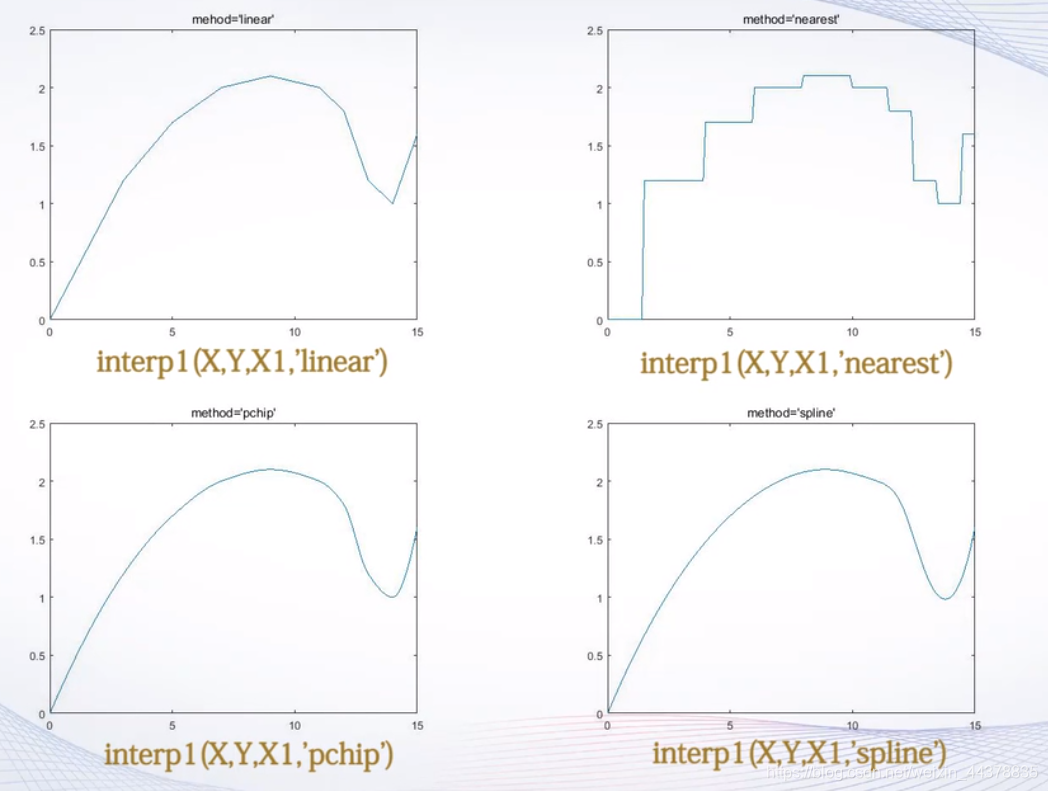
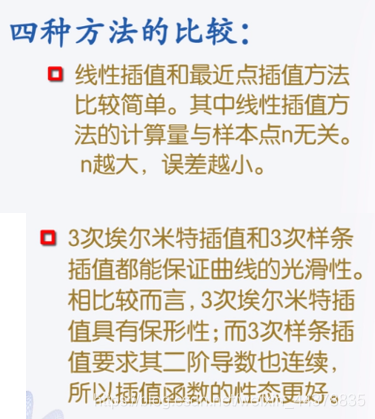
![在这里插入图片描述](https://img-blog.csdnimg.cn/2020022723045227.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227230609996.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227230738802.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227230828544.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)

D 曲线拟合(plotfit)

插值要求逼近函数在采样点的数值与原函数相等，然而在实验中，测量的数据不一定准确，如果强求逼近函数过样本点，显然是不合理的。使用曲线拟合可以避免这种情况。

D.a 引例-人口预测问题

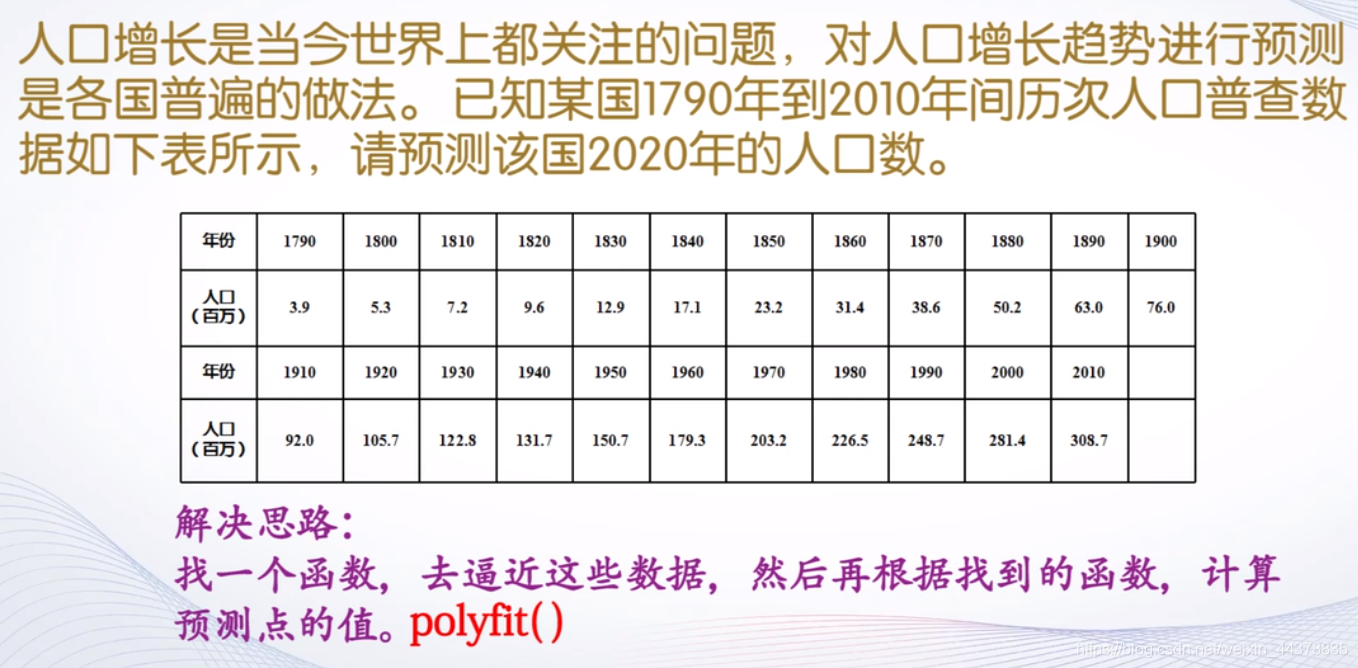
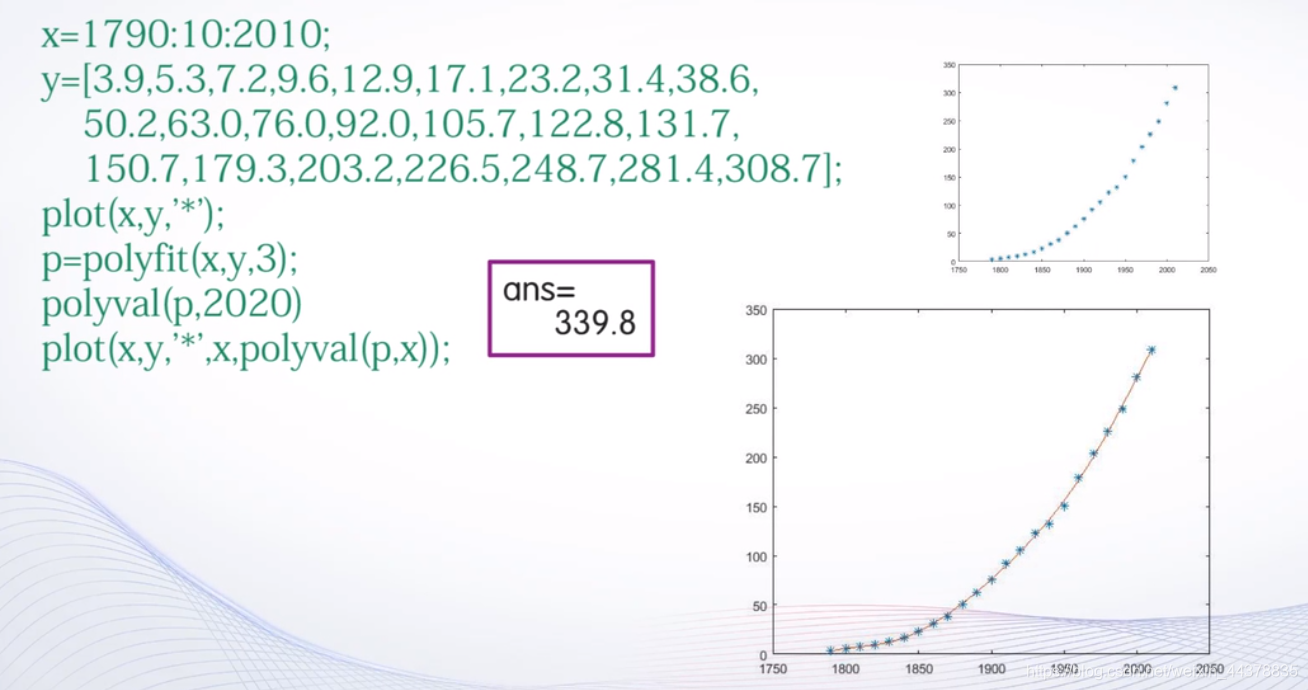
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227231750841.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/2020022723190549.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)

D.b 曲线拟合的原理

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227233203367.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227233315297.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ,size_16,color_FFFFFF,t_70)

D.c 曲线拟合的实现方法

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200227233521636.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDM3ODgzNQ==,size_16,color_FFFFFF,t_70)

图片来源：

https://www.icourse163.org/search.htm?search=中南大学 Matlab#/

在这里插入图片描述

posted on 2021-07-01 19:47  夜的独白  阅读(120)  评论(0)    收藏  举报