假设检验分为参数假设检验和分布拟合假设检验和非参数检验
一、假设检验的思想:
- 建立假设
- 选择检验统计量并给出拒绝域形式
- 选择显著性水平
- 给出拒绝域
- 做出判断
二、p 值:利用样本观测值能够作出拒绝原假设的最小显著性水平
三、参数假设检验类型:详见茆诗松
- 正态总体参数假设检验
- 指数参数假设检验,对指数分布的参数θ进行假设检验 2n x θ0
服从自由度为 2n 的卡方分布。
- 比率 p 的假设检验。二项分布参数 p 的假设检验。
- 大样本检验:构造正态分布统计量。
- 似然比检验 LRT :分子表示没有假设的似然函数最大值,分母表示在原假设成立下的似然函数最大值
四、分布拟合检验
1、卡方拟合优度检验:

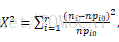
服从自由度为r-1的卡方分布
2、正态性检验
(1)正态概率图:样本点基本分布在正态概率图的一条直线上
(2) W 检验:当 8 ≤ n ≤ 50 时可以用, n 过小时对偏离正态分布的检验不太有效,n过大时计算一些辅助量比较麻烦。
PS: W统计量是n个数对(x(i),ai),i=1,2,3,4…的相关系数的平方,其中系数ai在不同的样本容量n可通过查系数得到。
(3)EP检验:出发点是利用样本的特征函数与正态分布的特征函数的差的模的平方产生的加权积分得到。



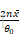 服从自由度为 2n 的卡方分布。
服从自由度为 2n 的卡方分布。
 浙公网安备 33010602011771号
浙公网安备 33010602011771号