2025.5.1
P10722 [GESP202406 六级] 二叉树
题目描述
小杨有⼀棵包含 $n$ 个节点的二叉树,且根节点的编号为 $1$。这棵二叉树任意⼀个节点要么是白色,要么是黑色。之后小杨会对这棵二叉树进行 $q$ 次操作,每次小杨会选择⼀个节点,将以这个节点为根的子树内所有节点的颜色反转,即黑色变成白色,白色变成黑色。
小杨想知道 $q$ 次操作全部完成之后每个节点的颜色。
输入格式
第⼀行一个正整数 $n$,表示二叉树的节点数量。
第二行 $(n-1)$ 个正整数,第 $i$($1\le i\le n-1$)个数表示编号为 $(i+1)$ 的节点的父亲节点编号,数据保证是⼀棵二叉树。
第三行一个长度为 $n$ 的 $\texttt{01}$ 串,从左到右第 $i$($1\le i\le n$)位如果为 $\texttt{0}$,表示编号为 $i$ 的节点颜色为白色,否则为黑色。
第四行⼀个正整数 $q$,表示操作次数。
接下来 $q$ 行每行⼀个正整数 $a_i$($1\le a_i\le n$),表示第 $i$ 次操作选择的节点编号。
输出格式
输出一行一个长度为 $n$ 的 $\texttt{01}$ 串,表示 $q$ 次操作全部完成之后每个节点的颜色。从左到右第 $i$($1\le i\le n$) 位如果为 $\texttt{0}$,表示编号为 $i$ 的节点颜色为白色,否则为黑色。
输入输出样例 #1
输入 #1
6
3 1 1 3 4
100101
3
1
3
2
输出 #1
010000
说明/提示
样例解释
第一次操作后,节点颜色为:$\texttt{011010}$
第二次操作后,节点颜色为:$\texttt{000000}$
第三次操作后,节点颜色为:$\texttt{010000}$
数据范围
| 子任务编号 | 得分 | $n$ | $q$ | 特殊条件 |
|---|---|---|---|---|
| $1$ | $20$ | $\le 10^5$ | $\le 10^5$ | 对于所有 $i\ge 2$,节点 $i$ 的父亲节点编号为 $i-1$ |
| $2$ | $40$ | $\le 1000$ | $\le 1000$ | |
| $3$ | $40$ | $\le 10^5$ | $\le 10^5$ |
对于全部数据,保证有 $n,q\le 10^5$。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n;
int a[N],b[N];
int to[N],ne[N],h[N],idx=0;
void add(int u,int v){
to[++idx]=v;
ne[idx]=h[u];
h[u]=idx;
}
void dfs(int u,int cnt){
// cout<<a[u]<<endl;
a[u]=a[u]^cnt^b[u];
// cout<<a[u]<<endl;
for(int i=h[u];~i;i=ne[i]){
int v=to[i];
dfs(v,cnt^b[u]);
}
}
int main(){
cin>>n;
memset(h,-1,sizeof h);
for(int i=2;i<=n;i++){
int x;
cin>>x;
add(x,i);
}
string s;
cin>>s;
for(int i=0;s[i];i++){
if(s[i]=='0') a[i+1]=0;
else a[i+1]=1;
}
// for(int i=1;i<=n;i++) cout<<a[i]<<' ';
// cout<<endl;
int q;
cin>>q;
while(q--){
int x;
cin>>x;
b[x]^=1;
}
dfs(1,0);
for(int i=1;i<=n;i++)
cout<<a[i];
return 0;
}
P2052 [NOI2011] 道路修建
题目描述
在 W 星球上有 $n$ 个国家。为了各自国家的经济发展,他们决定在各个国家之间建设双向道路使得国家之间连通。但是每个国家的国王都很吝啬,他们只愿意修建恰好 $n - 1$ 条双向道路。
每条道路的修建都要付出一定的费用,这个费用等于道路长度乘以道路两端 的国家个数之差的绝对值。例如,在下图中,虚线所示道路两端分别有 $2$ 个、$4$ 个国家,如果该道路长度为 $1$,则费用为 $1×|2 - 4|=2$。图中圆圈里的数字表示国家的编号。

由于国家的数量十分庞大,道路的建造方案有很多种,同时每种方案的修建费用难以用人工计算,国王们决定找人设计一个软件,对于给定的建造方案,计算出所需要的费用。请你帮助国王们设计一个这样的软件。
输入格式
输入的第一行包含一个整数 $n$,表示 W 星球上的国家的数量,国家从 $1$ 到 $n$ 编号。
接下来 $n–1$ 行描述道路建设情况,其中第 $i$ 行包含三个整数 $a_i,b_i$ 和 $c_i$,表示第 $i$ 条双向道路修建在 $a_i$ 与 $b_i$ 两个国家之间,长度为 $c_i$。
输出格式
输出一个整数,表示修建所有道路所需要的总费用。
输入输出样例 #1
输入 #1
6
1 2 1
1 3 1
1 4 2
6 3 1
5 2 1
输出 #1
20
说明/提示
对于 $100%$ 的数据,$1\leq a_i, b_i\leq n$,$0\leq c_i\leq10^6$,$2\leq n\leq 10^6$。
| 测试点编号 | $n=$ |
|---|---|
| $1$ | $2$ |
| $2$ | $10$ |
| $3$ | $100$ |
| $4$ | $200$ |
| $5$ | $500$ |
| $6$ | $600$ |
| $7$ | $800$ |
| $8$ | $1000$ |
| $9$ | $10^4$ |
| $10$ | $2\times 10^4$ |
| $11$ | $5\times 10^4$ |
| $12$ | $6\times 10^4$ |
| $13$ | $8\times 10^4$ |
| $14$ | $10^5$ |
| $15$ | $6\times 10^5$ |
| $16$ | $7\times 10^5$ |
| $17$ | $8\times 10^5$ |
| $18$ | $9\times 10^5$ |
| $19,20$ | $10^6$ |
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
int n;
int to[N],ne[N],h[N],w[N],idx=0;
void add(int a,int b,int c){
to[++idx]=b;
ne[idx]=h[a];
h[a]=idx;
w[idx]=c;
}
int siz[N];
int ans=0;
void dfs(int u,int fa){
siz[u]=1;
for(int i=h[u];~i;i=ne[i]){
int v=to[i];
if(v!=fa){
dfs(v,u);
siz[u]+=siz[v];
ans+=abs(n-siz[v]*2)*w[i];
}
}
}
int main(){
cin>>n;
memset(h,-1,sizeof h);
memset(siz,0,sizeof siz);
for(int i=1;i<n;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
add(b,a,c);
}
dfs(1,0);
// for(int i=1;i<=n;i++) cout<<siz[i]<<' ';
cout<<ans<<endl;
return 0;
}
P1661 扩散
题目描述
一个点每过一个单位时间就会向四个方向扩散一个距离,如图。
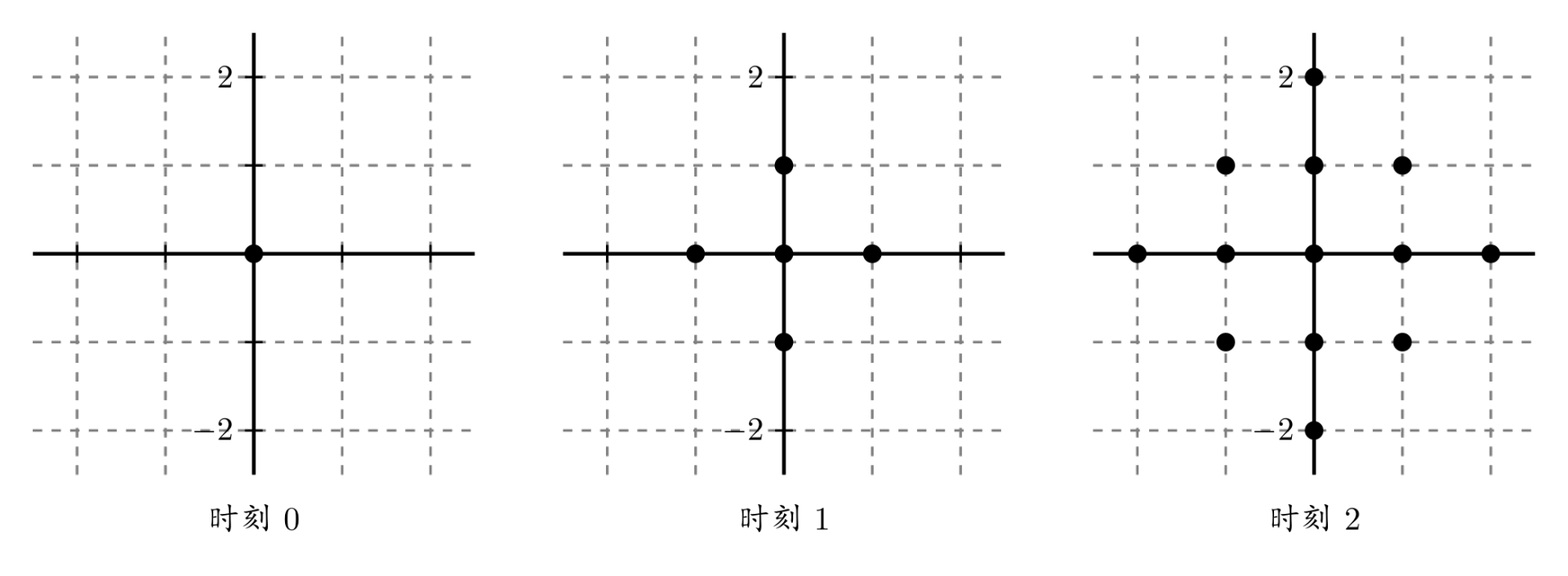
两个点 $a$ 、 $b$ 连通,记作 $e(a,b)$,当且仅当 $a,b$ 的扩散区域有公共部分。连通块的定义是块内的任意两个点 $u,v$ 都必定存在路径 $e(u,a_0),e(a_0,a_1),\cdots,e(a_k,v)$。给定平面上的 $n$ 个点,问最早什么时刻它们形成一个连通块。
输入格式
第一行一个数 $n$,以下 $n$ 行,每行一个点坐标。
输出格式
一个数,表示最早的时刻所有点形成连通块。
输入输出样例 #1
输入 #1
2
0 0
5 5
输出 #1
5
说明/提示
数据范围及约定
对于 $20%$ 的数据,满足 $1 \le N \le 5;1 \le X_i,Y_i \le 50$。
对于 $100%$ 的数据,满足 $1 \le N \le 50$,$1 \le X_i,Y_i \le 10^9$。
#include<bits/stdc++.h>
#define int long long
#define x first
#define y second
using namespace std;
pair<int,int> p[100];
struct edge{
int u,v,w;
};
vector<edge> e;
bool cmp(edge a,edge b){
return a.w<b.w;
}
int f[100];
int find(int x){
if(f[x]!=x) f[x]=find(f[x]);
return f[x];
}
signed main(){
int n;
cin>>n;
for(int i=1;i<=n;i++)
cin>>p[i].x>>p[i].y;
for(int i=1;i<=n;i++) f[i]=i;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
int dis=abs(p[i].x-p[j].x)+abs(p[i].y-p[j].y);
e.push_back({i,j,dis});
}
}
sort(e.begin(),e.end(),cmp);
int m=e.size();
int max_dis=0;
for(int i=0;i<m;i++){
int u=e[i].u,v=e[i].v;
int fu=find(u);
int fv=find(v);
if(fu!=fv){
f[fu]=fv;
max_dis=e[i].w;
}
}
cout<<(1+max_dis)/2<<endl;
return 0;
}
P1738 洛谷的文件夹
题目描述
kkksc03 是个非凡的空想家!在短时间内他设想了大量网页,然后总是交给可怜的 lzn 去实现。
洛谷的网页端,有很多文件夹,文件夹还套着文件夹。
例如:$\verb!/luogu/application/controller!$ 表示根目录下有一个名称为 $\verb!luogu!$ 的文件夹,这个文件夹下有一个名称 $\verb!application!$ 的文件夹,其中还有名为 $\verb!controller!$ 的文件夹。
每个路径的第 $1$ 个字符总是 $\verb!/!$,且没有两个连续的 $\verb!/!$,最后的字符不是 $\verb!/!$。所有名称仅包含数字和小写字母。
目前根目录是空的。kkksc03 想好了很多应该有的文件夹路径名。问题是,需要是使这些文件夹都存在,需要新建几个文件夹呢?
输入格式
输入文件第 $1$ 行为一个正整数 $N$。
接下来 $N$ 行,每行为一个描述路径的字符串,长度均不超过 $100$。
输出格式
输出应包含 $N$ 行,每行 $1$ 个正整数,第 $i$ 行输出若要使第 $1$ 个路径到第 $i$ 个路径存在,最少需要新建多少个文件夹。
输入输出样例 #1
输入 #1
2
/luogu/application/controller
/luogu/application/view
输出 #1
3
4
输入输出样例 #2
输入 #2
3
/chicken
/chicken/egg
/chicken
输出 #2
1
2
2
输入输出样例 #3
输入 #3
4
/a
/a/b
/a/c
/b/b
输出 #3
1
2
3
5
说明/提示
数据范围及约定
- 对于 $20%$ 数据,有 $N \le 20$;
- 对于 $50%$ 数据,有 $N \le 200$;
- 另有 $30%$ 数据,有对于所有路径最多存在两个 $\verb!/!$(包含第 $1$ 个字符);
- 对于所有数据,$N \le 1000$。
#include<bits/stdc++.h>
using namespace std;
int n;
int main(){
cin>>n;
set<string> st;
for(int i=1;i<=n;i++){
string s;
cin>>s;
string dir="";
for(int j=0;s[j];j++){
if(s[j]=='/') st.insert(dir);
dir+=s[j];
}
st.insert(dir);
cout<<(int)st.size()-1<<endl;
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
int n;
int main(){
cin>>n;
set<string> st;
for(int i=1;i<=n;i++){
string s;
cin>>s;
string dir="";
for(int j=1;s[j];j++){
if(s[j]=='/') st.insert(dir);
else dir+=s[j];
}
if(dir!="") st.insert(dir);
cout<<(int)st.size()<<endl;
}
return 0;
}
上述代码55/100原因在于/a/a和/aa混淆



 浙公网安备 33010602011771号
浙公网安备 33010602011771号