计算机考研之数据结构-树

数据结构-树

概念

定义

根结点只有一个
除根结点以外其他所有结点有且仅有一个前驱
所有结点都可以用任意个后驱

术语

以A-B-E-K路径为例：

祖先结点：结点到根结点路径上的所有前驱，A,B,E都是K的祖先结点。
子孙结点：结点的所有后驱，B,E,K都是A的子孙结点。
双亲结点：结点的直接前驱，E是K的双亲结点。
孩子结点：结点的直接后驱，K是E的孩子结点。
兄弟结点：相同双亲的结点，E,F是兄弟结点。
结点的度：结点的子结点个数。
树的度：结点的最大度数。
分支结点：度大于0的结点。
叶子结点：度等于0的结点。
结点的层次：从树根开始数层数。
结点的深度：自上向下。
结点的高度：自下向上。
树的高度（深度）：结点的最大层数。
有/无序树：结点的子树是否可以有序。
平衡/丰满树：除最底层，其他层都是满的。
森林：不相交树的集合。

性质

树的结点数等于所有结点的度之和+1。

二叉树

定义

最大度为2
可以为空
有序树

特殊

几个特殊的二叉树：

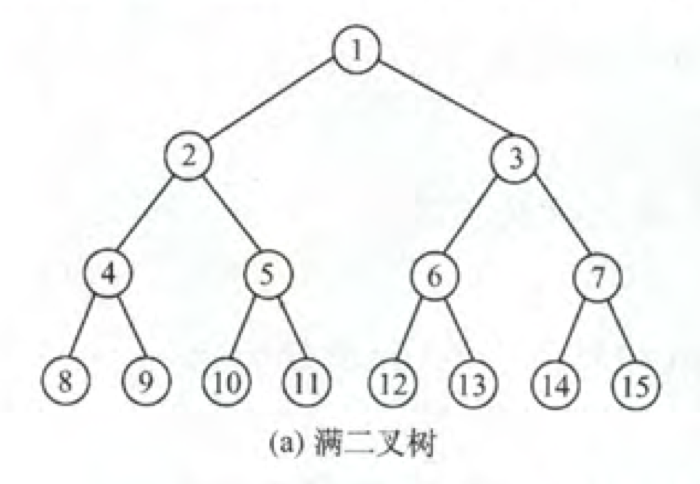
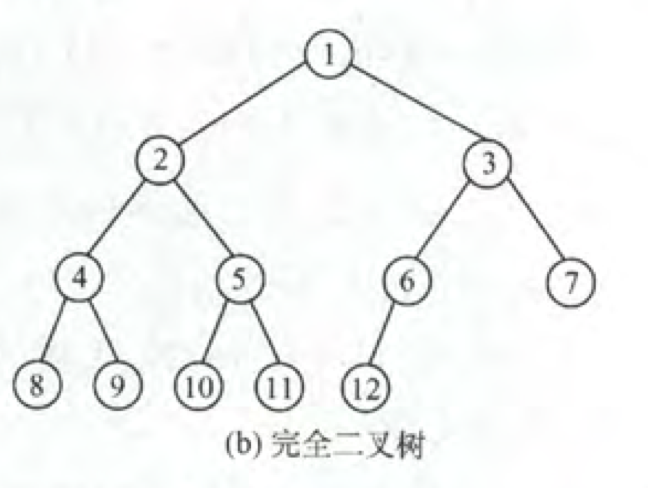
满二叉树：叶子结点都集中在最后一层的二叉树。
完全二叉树：如果对满二叉树的结点进行编号，如上图所示。编号连续的满二叉树子集称为完全二叉树。
二叉排序树：左子树结点的关键字均小于右子树的结点繁荣关键字。
平衡二叉树：树中任意一个结点的左右子树的深度差不超过1。

性质

非空二叉树上的叶子结点数等于双分支结点数加1。
二叉树第i层上最多有\(2^{i-1}\)个结点。
完全二叉树对各结点从上到下，从左到右分别从1开始进行编号则对\(a_i\)有：
1. 若i≠1，双亲结点编号为[i/2]。
2. 若2i≤n，a左孩编号为2i，反之无左孩。
3. 若2i+1≤n，a右孩编号为2i+1，反之无右孩。
  若0开始编号，双亲[i/2]-1，左孩2i+1，右孩2i+2。

存储

存储结构一般分两种，顺序或者链式。

顺序存储
因为我们已经知道了完全二叉树是满足一定性质的，这样即使是顺序存储也能很方便的找到其双亲和孩子结点。但是对于非完全二叉树的情况会很浪费存储空间。
链式存储

typedef struct BNode{
    int data;
    struct BNode *lchild;
    struct BNode *rchild;
}BNode, *BTree;

遍历

递归

遍历有先序，中序，和后序三种方式，区别在于访问根结点的顺序。
递归遍历比较简单，这里就举一个前序的例子。假设visit是对结点的操作。

void PreOrder(BTree T){ //先序遍历
    if(T==NULL) return;
    visit(T); //访问根结点
    PreOrder(T->lchild); //递归遍历左子树
    PreOrder(T->rchild); //递归遍历右子树
}

时间复杂度O(n)，空间复杂度O(n)。

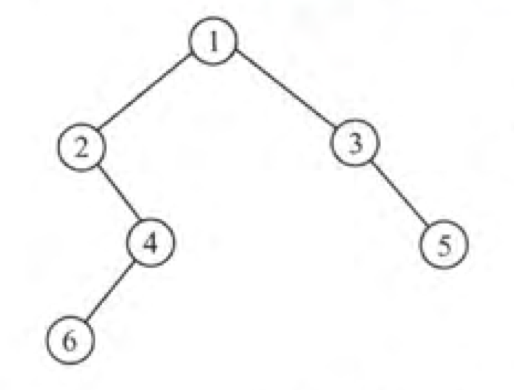
以上图为例：

前序：1 2 4 6 3 5
中序：2 6 4 1 3 5
后序：6 4 2 5 3 1

非递归

重点在于非递归的实现方式：

前序：
这里要利用到栈的性质，我们向左一直遍历树，然后保存这些左结点的，等遍历到了左下角，开始弹栈，转向遍历右结点。

void PreOrder(BTree T){
    InitStack(S); BTree p=T;
    while(p||!isEmpty(S)){
        while(p){
            visit(p);
            stack.push(p);
            p=p.lchild;
        }
        p=stack.pop();
        p=p.rchild;
    }
}

中序：
中序和后序唯一的区别就是：访问根结点的顺序不一样。

void PreOrder(BTree T){
    InitStack(S); BTree p=T;
    while(p||!isEmpty(S)){
        while(p){
            Push(S,p);
            p=p.lchild;
        }
        Pop(S,p);
        visit(p); // 弹栈后才访问根结点
        p=p.rchild;
    }
}

后序：
后序的情况稍微复杂一点。

void PreOrder(BTree T){
    InitStack(S); BTree p=T; BTree last=NULL;
    while(p||!isEmpty(S)){
        while(p){
            Push(S,p);
            p=p.lchild;
        }
        GetTop(S, p);
        if(p.rchild==NULL && p==last){
            visit(p);
            Pop(S);
            last=p;
            p=NULL;
        }
        else{
            p=p.rchild;
        }
    }
}

层次遍历

逐层遍历二叉树

void LevelOrder(BTree T){
    InitQueue(Q); BTree p;
    EnQueue(Q,T);
    while(!IsEmpty(Q)){
        DeQueue(Q, p);
        visit(p);
        if(p->lchild != NULL) EnQueue(Q, P->lchild);
        if(p->rchild != NULL) EnQueue(Q, P->rchild);
    }
}

遍历构造

给定前序+中序或者后序+中序的遍历序列，根据序列构造二叉树。注意：前序和后序不一定唯一确定二叉树。

BNode* create(vector<int> &inorder, vector<int> &postorder, int is, int ie, int ps, int pe){
    if(ps > pe){
        return nullptr;
    }
    BNode* node = new BNode(postorder[pe]);
    int pos;
    for(int i = is; i <= ie; i++){
        if(inorder[i] == node->val){
            pos = i;
            break;
        }
    }
    node->left = create(inorder, postorder, is, pos - 1, ps, ps + pos - is - 1);
    node->right = create(inorder, postorder, pos + 1, ie, pe - ie + pos, pe - 1);
    return node;
}

如果方便对数组进行切割的话，代码会更简单，举个例子：

def buildTree(self, inorder, postorder):
    if not inorder or not postorder:
        return None
    
    root = TreeNode(postorder.pop())
    inorderIndex = inorder.index(root.val)
    
    root.right = self.buildTree(inorder[inorderIndex+1:], postorder)
    root.left = self.buildTree(inorder[:inorderIndex], postorder)
    
    return root

注意如果是前序+中序的话，right和left的位置要调换。

线索二叉树

在二叉树中，存在大量空指针域，可以利用这些空指针域来加快遍历二叉树。

定义

线索规则：

若ptr->lchild为空，则lchild指向其中序遍历的前驱结点。
若ptr->lchild为空，则rchild指向其中序遍历的后继结点。

typedef struct ThreadNode{
    int data;
    struct ThreadNode *lchild, *rchild;
    int ltag, rtag;
}ThreadNode, *ThreadTree

这里的ltag和rtag用于指示指针指向的是子结点还是线索。

构造

在中序递归遍历中插入线索：

void CreateInThread(ThreadTree T){
    ThreadTree pre=NULL;
    InThread(T,pre);
    pre->rchild=NULL;
    pre->rtag=1;
}

void InThread(ThreadTree &p, ThreadTree &pre){
    if(p!NULL){
        InThread(p->lchild,pre); //线索化左子树
        
        // 线索化过程，除了线索化，其他跟普通的遍历二叉树一样
        if(p->lchild==NULL){
            p->lchild=pre;
            p->ltag=1;
        }
        if(pre!=NULL&&pre->rchild==NULL){
            pre->rchild=p;
            pre->rtag=1;
        }
        pre=p;
        // 线索化结束

        InThread(p->rchild,pre); //线索化右子树
    }
}

遍历

这里可以看出，二叉树被线索化之后近似于一个线性的结构。

//t指向头结点，头结点左链lchild指向根结点，头结点右链rchild指向中序遍历的最后一个结点。
//中序遍历二叉线索树表示二叉树t
int InOrder(BTree T)
{
    BTree *p;
    *p = t->lchild;                               //p指向根结点
    while(p != t)                               //空树或遍历结束时p == t
    {
        while(p->ltag == Link)                       //当ltag = 0时循环到中序序列的第一个结点
        {
            p = p->lchild;
        }
        printf("%c ", p->data);                      //显示结点数据，可以更改为其他对结点的操作
        while(p->rtag == Thread && p->rchild != t)
        {
            p = p->rchild;
            printf("%c ", p->data);
        }
 
        p = p->rchild;                         //p进入其右子树
    }
 
    return OK;
}

树与森林

转化

树转二叉树
树转化为二叉树可以理解为使用一个二叉链表来存储树的结构，使得链表中的指针一个指向自己的孩子结点一个指向自己的兄弟结点，这样这课树就表示成了二叉树。
这种存储结构一般称之为孩子兄弟存储结构。

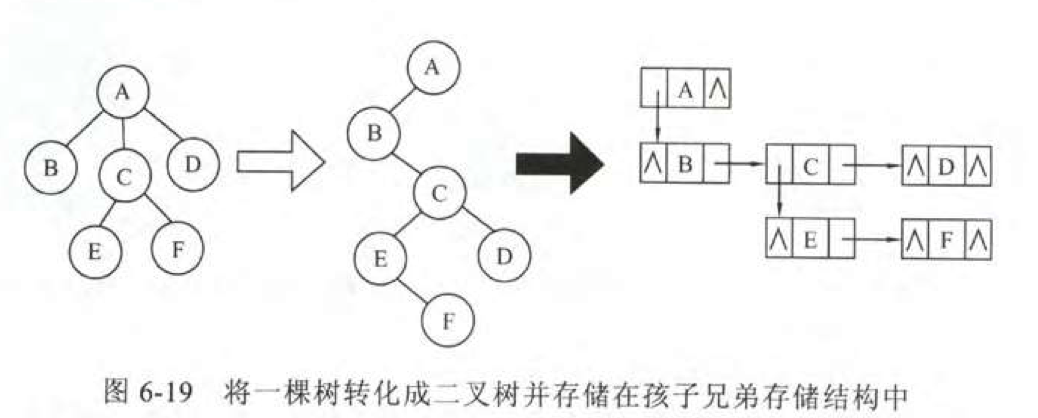
过程如下：

将同一结点的孩子串起。
将每个结点的分支从左到右除第一个以外全部剪掉。

二叉树转化树
这个其实就是树转二叉树的逆操作。

将二叉树从左上到右下进行斜向的分层。
为每层的结点找到父结点。
连接父结点，并删除层之间的结点连接。

森林转二叉树
根据孩子兄弟表示法，根结点是只有左孩子但是没有右兄弟的，所以可以把第二棵树接到第一个棵树的右孩上，第三棵树接到第二课树根结点的右孩上，以此类推。

先将森林中的树按照树转二叉树的步骤进行二叉树转化
将根结点的右孩与其他树进行拼接。

二叉树转森林

断开二叉树的右孩，重复此操作直到所有二叉树都没有右孩。
把这些二叉树按照二叉树转树的操作转化为树

遍历

树的遍历
遍历分先序和后序，也叫先跟和后根。区别在于对跟结点的访问在遍历子树之前还是之后。

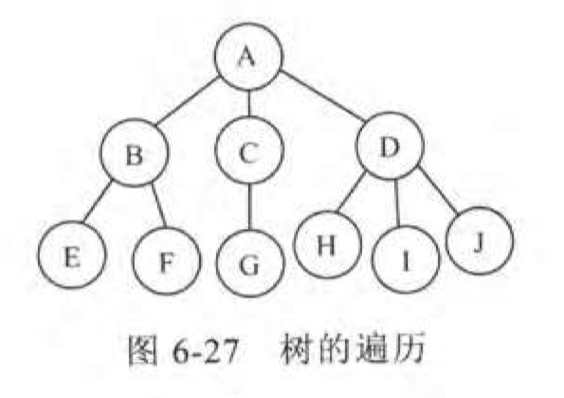
先序：ABEFCGDHIJ
后序：EFBGCHIJDA
当树转化为二叉树之后，树的先序对应二叉树的先序，树的后序对应二叉树的中序。

森林的遍历
森林遍历与树同理。

对于树与森林，中序遍历和后序遍历是一个意思。

哈夫曼树

概念

哈夫曼树是带权路径长度(WPL)最小的树。
那么首先明确带权路径长度(WPL)的概念。

\[WPL=\sum_{i=1}^nw_i\times l_i \]

w为结点的权值，l为路径长度。

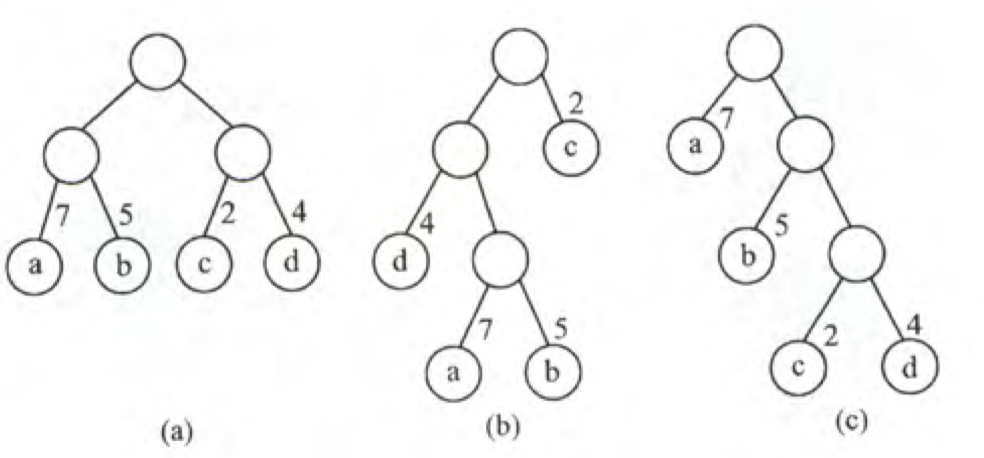
对于上图有WPL：
a: 7x2+5x2+2x2+4x2=36
b: 7x3+5x3+2x1+4x2=46
c: 7x1+5x2+2x3+4x3=35

构造

给定n个权值，利用这n个权值构造哈夫曼二叉树。

将这n的权值视作n棵根为n的树，记做F集合。
从F选择两棵根结点权值最小的树构造新的二叉树(新的根结点的权值等于两个根结点之和)。
从F删去这两个结点，并加入新结点。
重复2,3直到F中只剩一棵树。

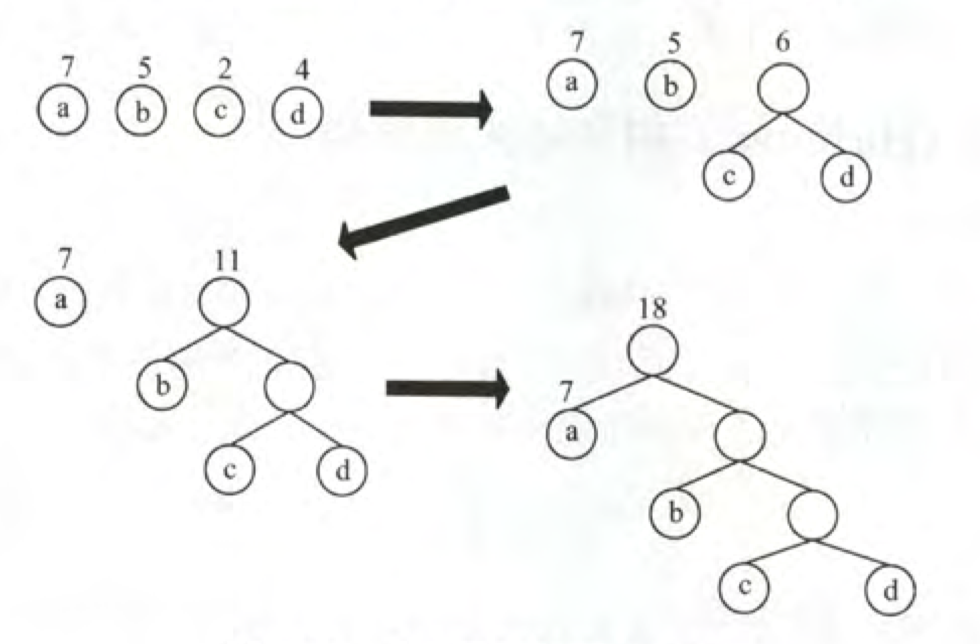
于是可以看出：

权值越大离根越近。
没有度为1的结点，也叫正则（严格）二叉树
树的带权路径最短

哈夫曼编码

哈夫曼树最常用的一个例子就是利用哈夫曼树进行文件压缩。
我们可以根据字符出现次序为其进行哈夫曼编码，次数越多越短，否则反之。
如果有一个文本，a出现了45次，b13,c12,f5,e9,d16。共100个。
可以构造得到哈夫曼树及其编码。

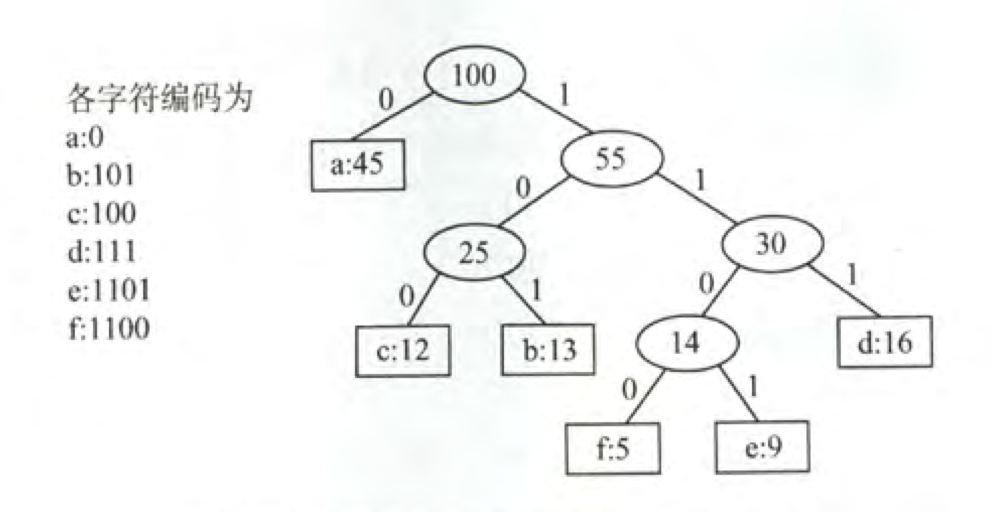
结点
计算WPL得到是224，比起3x100来压缩了76个字符的长度。

哈夫曼n叉树

注意哈夫曼树不一定是二叉树，也有可能是多叉树，但有可能需要0权值的结点来补齐，构造过程与二叉树区别在于从集合拿出树的个数。

小结

习题

在一棵度为4的树T中，若有20个度为4的结点，10个度为3的结点，1个度为2的结点，10个度为1的结点，则树T的叶结点的个数是():
答案：82
解析：
结点度数之和为：\(20\times 4+10\times 3+1\times 2+10\times 1=122\)。
树的结点数量为结点度数之和+1，即123个结点。
叶结点即度数为0的结点，度数大于0的结点数量为：\(20+10+1+10=41\)，总结点数量-度数大于0结点的数量，即82。

posted @ 2018-10-29 20:01 NeverMoes 阅读(3104) 评论(0) 编辑收藏举报

刷新页面返回顶部

SecondMind