21/7/3 读书笔记 MPC优化（电路结构和协议执行环节）贝叶斯定理 朴素贝叶斯分类 贝叶斯信念网络BBN

21/7/3 读书笔记

目录

安全计算导论 优化电路结构

电路的执行开销与电路的规模线性相关，尽可能减少电路的规模是提升电路效率的直觉选择。而在FreeXOR中，我们知道了XOR们对于MPC的重要意义，应用FreeXOR技术能够将XOR门的混淆开销降低到忽略不计的程度，故提升XOR门所占比例对于提升效率来说也是很重要的。

利用自动化工具能够很好地分析和优化电路结构：

  • CBMC：支持将C语言程序转换为门电路。通过将基础部件（加法器等）利用XOR门占优的方式进行优化，MPC效率显著提升
  • TinyGarble：针对时序电路，提出将时序状态单独作为额外的输入，每次重新计算，使得电路表示的整体规模减小。主要的目的在于期望减小RAM访问的开销，尽可能把电路相关的数据放在cache里

安全计算导论 优化协议执行环境

MPC协议的执行通常需要存储整个电路的所有混淆表，这降低了效率。Pipeline execution在初始阶段生成电路的结构，然后让电路的混淆表在真正使用到时生成，避免了存储所有的混淆表。

而更进一步，Compressing Circuits将电路的结构也进行压缩，采用Portable Circuit Format (PCF)的方式压缩，在协议执行过程中再解释出来。这种压缩方式同时也允许了我们对电路的多个子模块进行复用，进一步降低了表示电路的复杂程度。

Mixed Protocol则提出了混合多种多方计算协议，并举例使用同态加密协议，将原本需要复杂交流的MPC协议优化为简单的同态加密场景下的协作问题，以更好地提高计算效率。Outsourcing MPC更是提出利用outsourced computation，将计算负担分配给计算性能优异的参与者，而提高整体协议的执行效率。

数据挖掘导论 最近邻分类

最近邻分类是传统的消极学习方法。相对的，决策树归纳法、基于规则的分类方法都是需要从数据中进行建模，称之为积极学习方法。在最近邻分类法中，当我们对一个数据进行分类时，才会去遍历数据来选出最近邻对象。

最近邻分类思想是简单易懂的，在此不再赘述。我们需要清楚最近邻分类法的特点：

  • 区别于积极学习方法的全局分类决策，最近邻分类法表现出一种局部分类决策，即只有一小片空间内的数据对最后分类结果产生决定性作用
  • 最近邻分类器的决策边界非常灵活，在空间内展示出很高的可变性。其可变性有赖于训练样例的组合情况。
  • 最近邻分类器中距离的计算方法决定了最终分类的准确度

数据挖掘导论 贝叶斯定理 朴素贝叶斯分类器 贝叶斯误差

首先我们需要了解贝叶斯定理，先验概率(prior probability)和后验概率(posterior probability)。

假设小明考及格的概率是\(P(A)\)，相对的，不及格概率为\(P(\neg A)=1-P(A)\)。而我们已知小明及格的那天下雨的概率为\(P(B|A)\)。而今天下雨了，我们如何估计下雨的前提下小明的及格概率\(P(A|B)\)？

贝叶斯定理指出：

\[P(A|B)=\frac{P(A)P(B|A)}{P(B)} \]

这里我们称\(P(A)\)是先验概率，其展示出在没有条件前提下小明及格的概率，即事件发生前；\(P(A|B)\)是后验概率，其展示出事件发生后，相关条件已知的前提下，对结果的估计。

基于贝叶斯定理，首先提出的是朴素贝叶斯分类器：

朴素贝叶斯分类器的一个关键假设在于 所有属性间相对独立。这个假设使得对于事件集合\(B=\{b_1,b_2...\}\)来说:

\[P(B|A)=\prod_{i=1}^n P(b_i|A) \]

对离散属性，我们将属性\(x_i=特定值\)称为事件\(b_i\)；对连续属性，我们将\(x_i\in [特定区间]\)称为事件\(b_i\)；将对象归类为类\(a\)称为事件\(A\)，将所有\(b_i\)事件的合取称为事件\(B\)，故朴素贝叶斯分类器的工作原理被描述为：

\[P(A|B)=\frac{P(A)\prod_{i=1}^nP(b_i|A)}{P(B)} \]

我们通过计算出当前属性组合下概率最大的类标签从而进行分类。

其中对于连续属性的概率估计问题，我们将连续属性视作服从某种概率分布，然后利用相应的概率密度函数在一个长度趋近无穷小的区间\(\varepsilon\)内求积分，由于\(\varepsilon\)对于所有连续属性概率的求取都是取同一个值，因此不会影响最后概率的对比。

描述贝叶斯分类的决策边界，主要是看概率密度分布。当属于两个类的概率曲线（可能是高维曲线）相交，相交处对应的属性集合就是其分类边界。我们将这个边界以下的相交区域算作贝叶斯分类的总误差率，在这个区域内的属性集合对应的点可能同时属于两个类。贝叶斯误差率与两个分类曲线的相近程度高度相关，在属性空间内越类似，总误差率越大。

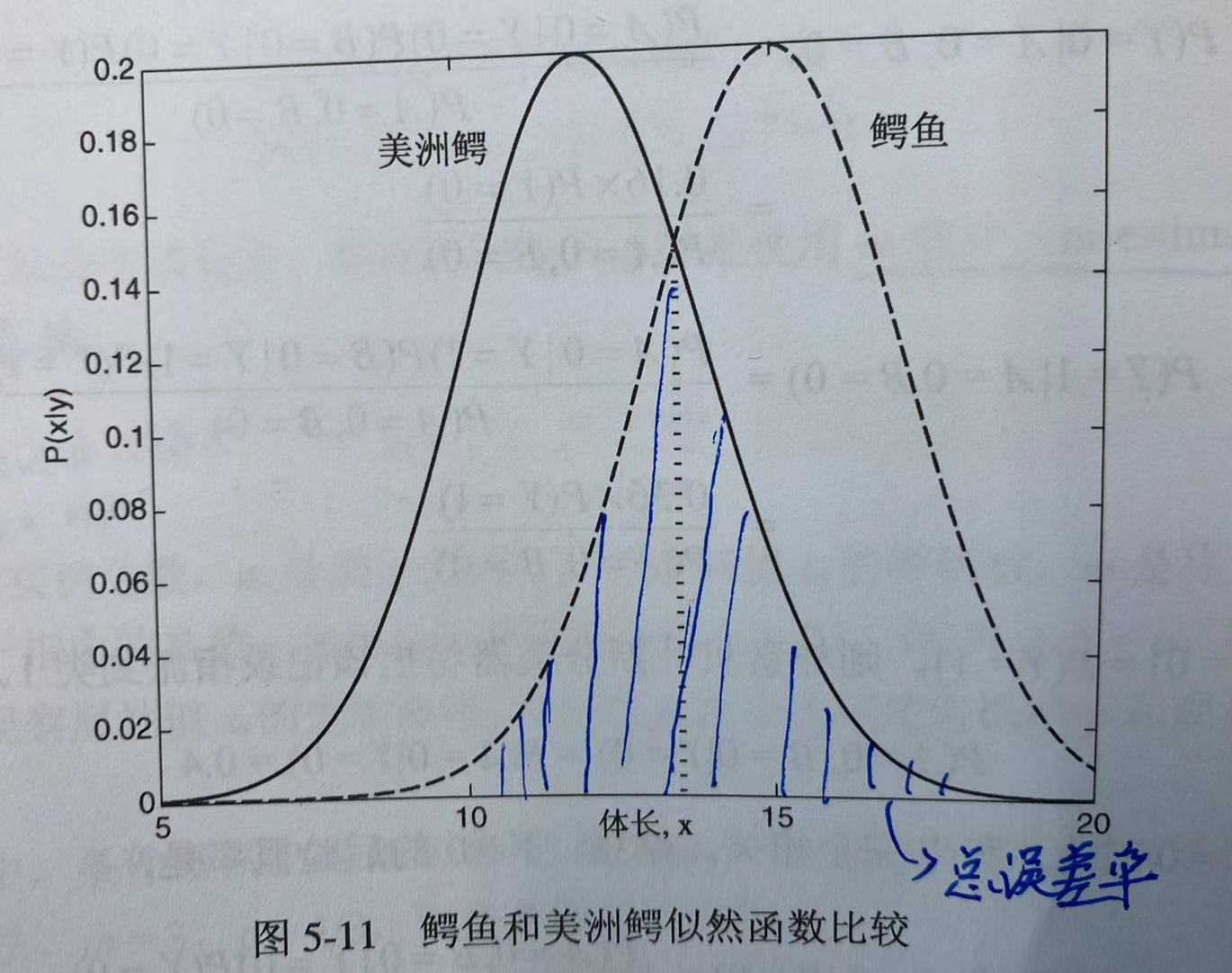
image-20210703095434533

朴素贝叶斯分类器的特征主要在于：

  • 对于孤立的噪声点、遗漏属性等，表现出较强的健壮性。因为估计条件概率是从统计角度进行求取的，因此这些噪声点造成的影响被平均
  • 无法处理属性间相互关联的情况因为朴素贝叶斯分类器在处理多个属性时的一个重要假设在于属性间的条件概率能够直接相乘，而这一点对于相互关联的属性来说并不成立

这里我们继续介绍贝叶斯信念网络（Bayes Belief Networks, BBN）。在BBN中不要求所有属性都相对独立，而是可以指定哪些属性是条件相对独立的。

BBN的核心在于使用图的方式表达了属性间的相关关系。我们描述这样一幅有向图，其中每个结点对应一个属性和一个概率表，每个有向边对应一个关联关系。我们定义这个图具有以下性质：

  • 对每个结点，如果其父母结点已知，则其条件独立于任何非后代结点
  • 对每个结点，
    • 如果其没有父母结点，那么其概率表只包含其先验概率
    • 如果有父母结点，那么其概率表包括父母结点分别取各个可能值时的条件概率

贝叶斯信念网络的构建过程与人工的专业知识和先验知识有关。我们对属性的全序集合做遍历并做以下操作：

  1. 按顺序取出一个属性元素
  2. 取排在该属性前的所有属性，利用人工专业知识和先验知识排除与该属性无关的属性
  3. 从排出后剩下的属性对应结点构建有向边到该属性对应结点，并给该属性对应结点的概率表赋值

对于BBN的推理基于从父母结点求取子结点的后验概率符合贝叶斯定理的，而不用担心父母结点间具有关联性。对\(\{A\to B, A\to C,B\to D, C\to D\}\)来说，也许从事实上B和C是有关联的，但是在求取过程中其关联关系已经通过结点A体现了，因此在通过B、C计算D时就可以忽略其关联关系了。通过递归地求取先验和后验概率就能得出最终任意结点在其他属性确定时的后验概率。

贝叶斯信念网络的特点在于：

  • 提供了图模型来描述特定领域的先验知识，揭示依赖关系，可解释性强
  • 添加变量很容易，只需要添加新结点和概率表即可，无需改变原有网络结点和概率表
  • 将数据和先验知识以概率的方式结合，对过拟合问题非常鲁棒
  • 对不完整的数据处理起来很方便，只需要通过求取所有可能取值来从逻辑上“跳过”该结点即可
posted @ 2021-07-03 10:24  neumy  阅读(409)  评论(0)    收藏  举报