21/6/28 读书笔记 姚氏混淆电路协议GC 数据预处理简析 数据的相似和相异
21/6/28 读书笔记
安全多方计算 基础MPC协议之GC
接下来展示的MPC协议都只针对semi-honest adversary情景:
姚氏混淆电路协议 Yao's Garbled Circuits Protocol
又称GC,其中参与者为双方,执行回合数(rounds)常数级,支持布尔运算。GC是很多MPC协议的基础,其表现优异,即使其通信复杂度并不是最好的,但是其常数级的rounds使得其不因circuit而改变。
我们考虑一个函数\(F(x,y)\),其值域X和Y均有限且离散。对每对输入<x,y>,我们认为\(F(x,y)\)可以被表示为一个二维表格\(T\)。其中\(T_{xy}=F(x,y)\)。对于两个参与者P1和P2,P1持有X,P2持有Y。当需要计算\(F(x,y)\)时,P1首先对整个表格\(T\)进行加密,即对每个\(T_{xy}\),分别提供密钥\(k_x\)和\(k_y\),并将其加密。由于P1知道自己提供的x的具体值,故能够给出唯一的\(k_x\),但是由于P1并不知道P2会提供哪个y,因此P1需要给出所有的\(k_y(y∈Y)\)。P1给出整个表格\(T\)(乱序的)、唯一的\(k_x\)、一组\(k_y\),其中\(k_y\)基于不经意传输(OT)进行传递。P2得到表格\(T\)和\(k_x\),并经过不经意传输得到唯一的\(k_y\),此时对于表格\(T\)中所有元素,只有一个元素能够被解密成功,即<x,y>对应的\(T_{xy}\)。
这里有一个小问题,就是P2只有遍历所有可能的元素才能找到目标,但是P2并不知道真正的目标长什么样子,也不知道自己是否解密了正确的元素。因此需要在正确信息中添加一定的识别码,如果解密结果没有识别码就说明解密错误,解密的结果应该被抛弃。
还有一种称为Poing-toPermute的改进方式(1990),其中P1给出的表格\(T\)经过了重排(Permute),然后在\(k_x,k_y\)中包含一定的指向重排后的\(T\)中特定元素的指针信息。这样P2就能通过两个密钥找到并解密特定的元素。
对于电路的情景,我们将P1和P2视作一个大的计算电路的两个部分,两者间存在多条wire传递信息。对于每个wire,其可能取0或者1,P1各自为其设置一个密钥\(k_0\)和\(k_1\)。实际电路执行过程中,一个wire要么是0要么是1,我们称这个确定的实际值是active value,对应的密钥为active label。对于一个gate,其有两个输入wire,对应\(k_i\)和\(k_j\)两个active label,有一个输出wire,对应一个active label \(k_o\)。我们对这个gate构造一张表(假设gate的性质可以用G(i,j)描述):
其中\(k_i^0\)表示i号wire在取0时对应的密钥,又或者可以称为i号wire对应0的active label
P1将这个\(T_G\)混淆(重排)后,搭配active label发送给P2。对于这个gate,P2既不知道其输入,也不知道具体的输出,它能够得到的只有这个gate输出的对应的active label,再将这个label传递给下一次gate计算。对于P2,其最终能够得到的只有最终结果所处wire的active label,这个值随后会被发送给P1。P1知道这个active label对应于什么值,故能够得到最终的结果。
以下面这个电路为例,假设1、2、3号wire的实际输入分别为A,B,C,其中A和C来自于P1的输入,B是P2的输入,来模拟一下整个MPC的过程:
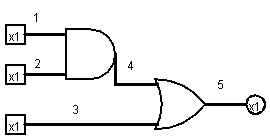
- P1将\(k_1^A\),\(T_{AND}\),以及2号wire对应的两个wire label(\(k_2^0,k_2^1\))发送给P2
- P2通过OT得出\(k_2^B\),然后根据\(k_1^A\),\(T_{AND}\)计算出4号wire的active label \(k_4^{AND(A,B)}\)。P2将这个label发送给P1。
- P1通过查询wire label(\(k_4^0,k_4^1\))从而知道4号wire的实际值为AND(A,B),而其已知3号wire的输入为C,故将\(k_3^C\)和\(T_{OR}\)发送给P2。(注意这里即使P1知道输入A和输出C,但是它仍然不能确定P2的输入B)
- P2知道\(k_4^{AND(A,B)}\),然后根据\(k_3^C\)和\(T_{OR}\)计算得出5号wire的active label \(k_5^{OR(AND(A,B),C)}\)并返回给P1
- P1通过查询wire label(\(k_5^0,k_5^1\))得到了最后的结果E
在这个过程中,P2一直都是懵逼的,它只是得到了所需要的wire的active label,但是并不知道这些label的明文对应着什么。P1没有进行电路的实际计算,而是构建和加密了所有gate的表,计算由P2隐性地执行了。GC将P2变成了完全的工具人!(x
如果你足够细心的话,可以从上面描述的过程中发现一些问题。在计算时,P1实际上并不需要多次和P2间进行交流,而是一次性将所有的需要的数据发送给P2,而只查看结果即可。上面描述的过程旨在展示这种方式在处理中间变量(intermediate wire)时也适用。在上述过程中的AND门计算中就涉及中间变量4号wire,P1似乎能够靠一个输入和输出(4号wire)推算出另一个来自P2的输入,但是这种情况在面对复杂电路时一般是不考虑的。
数据挖掘导论 数据预处理
数据预处理的形式有多种,方法也非常繁多,其中主要的思想和方法包括:
- 聚集:通过将多个对象合并为一个对象,实现对于数据集的压缩。聚集可以减少实际数据集的大小,改变数据集的宏观程度,改变行为的稳定性(比如年平均值通常比月平均值更加稳定)。但是会丢失一些可能的细节,比如一个月里哪几天的销售额明显更高。
- 抽样:选择数据集子集进行分析。需要进行有效抽样,即抽取的子集具有和原数据集一样的感兴趣的性质。对于需要考虑稀有对象时,可以采用分层抽样的方式。抽样的大小通常决定了抽样带来的信息损失情况,可以采取渐进抽样(自适应抽样),即动态改变抽样规模直到预测成功率稳定在可接受的值。
- 维归约:维度描述了对象属性的复杂程度。当维度过高时将引发维灾难,数据在某些维度空间变得越发稀疏,使得很多数据分析方法失去意义。通过创建新的属性来将一些(相关联的)旧属性合并,进而减少数据的维度。创建新属性的方法有特征选择法和线性代数技术。前者从旧属性中直接挑选出一个子集作为新属性,后者通过主成分分析(PCA)等线性代数的方法将原属性进行线性组合,进而得出相互正交的新属性(即使新属性看起来没有任何实际意义)。
- 特征选择或特征子集选择:用于维归约的方法,通常致力于减少冗余特征和不相关特征。前者指一些关联性较强的属性,以至于完全其中一者可以替代另一者;后者指与所感兴趣的特征相关性低的属性,比如在考察学生成绩时的学生ID属性就是不相关特征。
- 特征子集的选择方法包括嵌入、过滤和包装三种。其中嵌入依赖于具体的数据挖掘算法(通常在构造决策树分类器时)。过滤和包装在选择特征子集的过程上一致,都是搜索-评估-验证或再搜索,只是所采用的评估方法不同:
- 过滤:利用独立于数据挖掘任务的方法,在数据挖掘之前进行特征选择。
- 包装:利用数据挖掘算法本身作为黑盒,搜索并测试最优或较优的特征子集
- 特征加权:区别于直接放弃某些特征,而是对不同特征置不同权重,使得不同属性在数据挖掘过程中起到不同作用。
- 特征子集的选择方法包括嵌入、过滤和包装三种。其中嵌入依赖于具体的数据挖掘算法(通常在构造决策树分类器时)。过滤和包装在选择特征子集的过程上一致,都是搜索-评估-验证或再搜索,只是所采用的评估方法不同:
- 特征创建:通过原来的属性创建新的属性集合,新的属性集可能更小(实现了维归约),且能更有效捕获数据间的信息。包括三种创建新属性的相关方法:
- 特征提取:对某些基本数据,比如图像,其像素可能并不能直接得出什么信息。此时我们通过某些技术从这些基本的数据中提取出某些特征(比如是否包含人脸),然后利用这些提取的特征进行数据挖掘。特征提取的方式依赖于具体的数据场景,而与数据挖掘本身关系不大。
- 映射数据到新的空间:采用新的视角看待问题,比如对于某些包含复杂周期和噪音的时序数据,提取其中的频率特征可以有效表现出其中的周期规律。和特征提取的区别在于其提取的方式更具有普遍性。
- 特征构造:对于我们所感兴趣的信息而基于现有属性进行构造,比如我们希望按照制造材料进行产品分类,故将质量和体积特征重新构造为密度特征。这种构造或许能由数据挖掘算法本身发掘出来,但是如果能在预处理时就指出这个关系则能大幅提高挖掘效率和质量。
- 离散化和二元化:将原本连续或离散的值进一步离散或二元化,这对于某些数据挖掘算法(尤其是分类算法)有较好的效果。离散化方法分为监督和非监督量:
- 监督情况下,我们考虑属性本身的性质并通过人工的方式制定连续值的分割区间问题。通常采用熵分析法。
- 非监督情况下,我们可以考虑使用等宽、等频率、K-均值等方式决定分割区间问题。当然由于没有考虑数据本身的实际意义,有可能导致一些尴尬的结果,比如对于系号,6和21属于同类院系,却和5、4、3等划分为同类。
- 变量变换:对于数据中的某属性,同时对所有对象的该属性进行某些变换,使其能够更好体现所需要的信息。变量的变换通常是为了改变数据的特性从而使得数据本身能够更加符合需求。比如对收入而言,一天100和一天1000之间的差异的意义大于一天1亿和一天2亿,但是后者间的差距更大,更容易被挖掘算法捕获,因此我们需要进行一定的转化。变量变换包括两种方法:
- 简单函数:对变量进行一些简单的变换,比如求对数、指数等,使其在数据特性上发生改变。这种改变的前提在于充分了解数据和目标需求间的关系,变换方式严重依赖于实际意义,不恰当的变换会导致适得其反。
- 规范化和标准化:这两个是一个意思,为了使得变量的整个集合具有某些特定性质,比如将一个跨度很大的变量集合通过标准化形成均值为0、标准差为1的变量集合。这也有利于降低极端值、离群点带来的影响(当然,在你需要避免他们的前提下)
数据挖掘导论 相似性和相异性的度量
相似度和相异度描述了对象间的相似和差异程度,两者间可以相互变换。我们采用邻近度来统一描述这两个问题。邻近度的度量和具体的属性的数据类型有关:
- 对于标称,对象之间要么完全一致,要么不同
- 对于序数、区间、比率,通常与对象间差值有关
距离:距离是具有特殊性质的相异度,定义闵可夫斯基距离:
当r=1时为曼哈顿距离,r=2是为欧几里得距离(\(L_2\)范数),r=∞时表示对象属性间的最大距离(上确界,\(L_{max}\)范数)
我们将度量(metric)基于以下三点进行定义,对函数d(x,y):
- 非负性:对于任何x与y,d(x,y)>=0;当且仅当x=y时,d(x,y)==0
- 对称性:对于任何x与y,d(x,y)==d(y,x)
- 三角不等式:对于三个对象x、y、z,d(x,z)<=d(x,y)+d(y,z)
可见距离本身是一种度量
对于相似度,度量中的三角不等式通常不成立,而保持其他两条性质。
一些描述相异度和相似度的例子
对于二元数据(即每个属性都是0或者1),有两个邻近度评价方式:
-
简单匹配系数(Simple Matching Coefficient):
\[SMC=\frac{属性值相匹配的数目}{属性个数} \] -
Jaccard系数:对于非对称属性,SMC很可能判定相似性过高(因为大家很多都是相同的无意义的0)。定义:
\[J=\frac{匹配的个数}{不涉及0-0匹配的个数} \]
而推广到非对称的非二元数据中,我们不仅需要像Jaccard系数一样忽略0-0匹配,还需要能够应对更多元的向量,提出余弦相似度:
||x||表示对象向量的长度,即各属性数据通过勾股定理求长度(而不是指属性的个数!)。余弦相似度实际上通过对象向量空间内两者间的余弦值描述相似程度。
而另一方面也可以基于Jaccard系数给出广义Jaccard系数(又称Tanimoto系数),其表示为:
而从更加广义的统计角度上看,我们在考察线性相关性时引入皮尔森相关系数:
该系数常在-1~1间取值,1表示完全正相关,-1表示完全负相关,0表示不存在线性相关关系(但是不否认非线性相关)
邻近度计算中的普遍问题
- 距离度量的标准化和相关性:标准化是因为在属性的值域不同时,值域大的属性将左右距离度量(比如同时考虑年龄和收入),故需要对值域进行标准化。相关性是指属性间存在相关性且值域不同时,欧几里得距离相同的对象间的差异程度可能不同,此时采用Mahalanobis距离来衡量两个对象的距离。其将不同属性间先按照主成分旋转以使得属性之间独立,再进行标准化。
- 组合异种属性的相似度:组合异种属性指一个对象同时拥有定性和定量的属性。我们针对每个属性单独考虑其相似度,然后通过一定方式进行组合,同时考虑非对称属性而忽略0-0匹配。
- 在权重条件下的邻近度计算:有时我们对不同属性赋予了不同的权重以更好反映各个属性对于问题的重要程度。通常权重和为1,我们在计算距离时的对每个属性计算差距时添加对应权重。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号