代码随想录——二叉树21、合并二叉树（附：递归算法复杂度分析）

思路

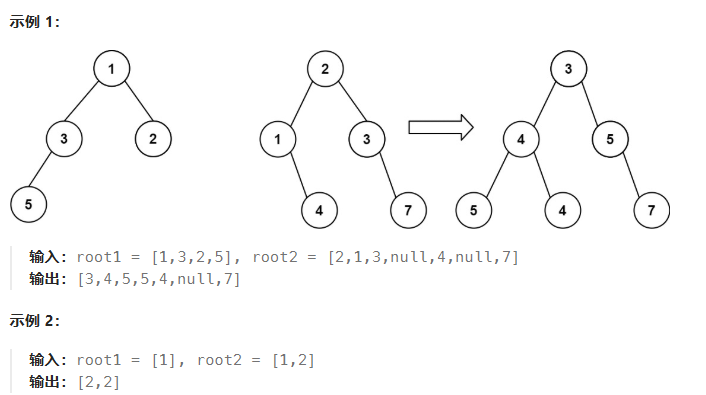
本题难点在于：如何同时遍历两棵二叉树。

方法和遍历一颗二叉树类似，只是同时传入两棵二叉树的节点。

代码

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1 == nullptr && root2 == nullptr)return nullptr;
        if(root1 == nullptr)return root2;
        if(root2 == nullptr)return root1;

        //如果都不空
        TreeNode* node = new TreeNode(root1->val + root2->val);
        node->left = mergeTrees(root1->left,root2->left);
        node->right = mergeTrees(root1->right,root2->right);

        return node;
    }
};

递归算法复杂度分析

递归算法的时间复杂度一般需要通过以下步骤计算：

1. 分析递归树：确定递归调用的次数和规模。
2. 计算单次递归的时间复杂度。
3. 结合递归调用次数和单次复杂度，得出总时间复杂度。

以本题为例：

1. 分析递归树：递归的总次数与两个输入树的节点数相关。
   因为只有两个树对应节点都不为空时才访问，设两棵树节点数分别为m,n，所以递归总次数为O(min(m，n))
2. 在递归中，每次递归调用的时间复杂度为 O(1)。
3. 总时间复杂度就是O(min(m,n))

空间复杂度主要由递归调用栈的深度决定：

这里都视一进递归函数就被return的情况不算一次递归调用