理解常见优化算法
摘要：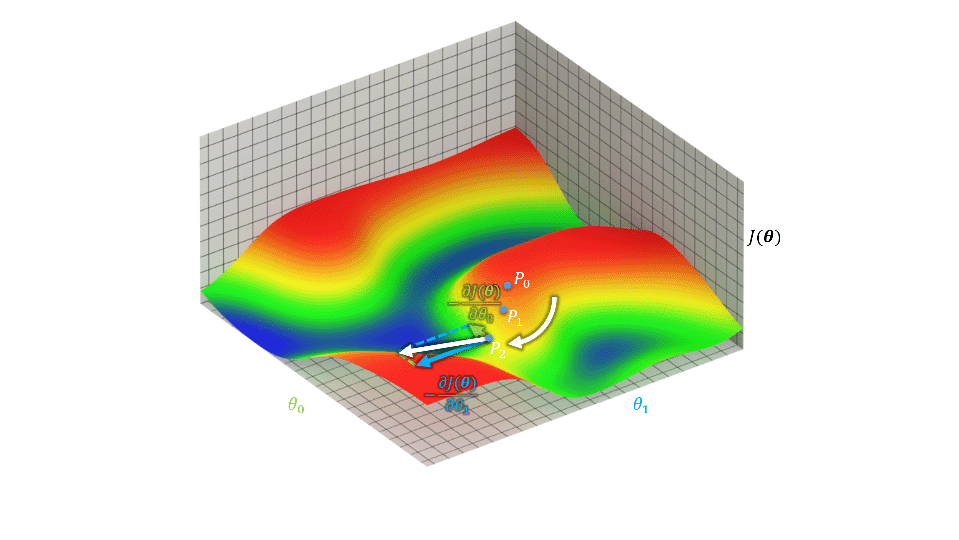 
梯度：梯度是矢量，设函数$f(x_0,x_1,\cdots,x_n)$在空间中有一阶连续偏导数，对空间中的点$P(a_0,a_1,\cdots,a_n)$有向量$\vec{g}=(\frac{\partial f}{\partial a_0},\frac{\partial f}{\partial a_2},\cdots,\frac{\partial f}{\partial a_n})$，$\vec{g}$即为$P$的梯度，$\nabla_{\vec{a}} f=\nabla f(a_0,a_1,\cdots,a_n)=\vec{g}$。计算输出$\hat{y}=f_\boldsymbol{\theta}(\boldsymbol{X})=\sum_{i=0}^{n}\theta_i x_i=\boldsymbol{\theta}^T\boldsymbol{X}$，其中$\boldsymbol{\theta}$为参数，$\boldsymbol{X}=\begin{bmatrix} x_0 & x_1 & \cdots & x_n \end{bmatrix}^T$… 阅读全文
梯度：梯度是矢量，设函数$f(x_0,x_1,\cdots,x_n)$在空间中有一阶连续偏导数，对空间中的点$P(a_0,a_1,\cdots,a_n)$有向量$\vec{g}=(\frac{\partial f}{\partial a_0},\frac{\partial f}{\partial a_2},\cdots,\frac{\partial f}{\partial a_n})$，$\vec{g}$即为$P$的梯度，$\nabla_{\vec{a}} f=\nabla f(a_0,a_1,\cdots,a_n)=\vec{g}$。计算输出$\hat{y}=f_\boldsymbol{\theta}(\boldsymbol{X})=\sum_{i=0}^{n}\theta_i x_i=\boldsymbol{\theta}^T\boldsymbol{X}$，其中$\boldsymbol{\theta}$为参数，$\boldsymbol{X}=\begin{bmatrix} x_0 & x_1 & \cdots & x_n \end{bmatrix}^T$… 阅读全文
posted @ 2021-09-22 19:27
星云*
阅读(238)
评论(0)
推荐(0)
机器学习监督学习常见算法。混合高斯模型GDA、朴素贝叶斯NBM、神经网络NN、支持向量机SVM各种公式。斯坦福公开课。 
HTML脚本绘制极坐标渐变。 
浙公网安备 33010602011771号