BZOJ4816 Sdoi2017数字表格

一开始只推出O(TN)的做法，后来看了看发现再推一步就好了。

我们只需要枚举gcd就可以啦。

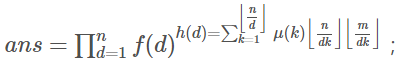
然后我们改变一下枚举顺序 

设T为dk

预处理中间那部分前缀积就好了。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=1e6+10,mod=1e9+7;
 4 int n,m,p[N/2],miu[N],g[N],f[N],inv[N],cnt;bool v[N];
 5 typedef long long ll;
 6 int qmod(int x,ll y)
 7 {
 8     int ans=1;
 9     while(y)
10     {
11         if(y&1)ans=1ll*ans*x%mod;
12         x=1ll*x*x%mod;y>>=1;
13     }
14     return ans;
15 }
16 void init()
17 {
18     miu[1]=1;
19     for(int i=2;i<=1e6;++i)
20     {
21         if(!v[i])
22         {
23             p[++cnt]=i;miu[i]=-1;
24         }
25         for(int j=1;j<=cnt&&i*p[j]<=1e6;++j)
26         {
27             v[i*p[j]]=1;
28             if(i%p[j]==0)break;
29             miu[i*p[j]]=-miu[i];
30         }
31     }
32     for(int i=1;i<=1e6;++i)g[i]=1;
33     f[0]=0;f[1]=g[0]=1;
34     for(int i=2;i<=1e6;++i)f[i]=(f[i-1]+f[i-2])%mod;
35     for(int i=1;i<=1e6;++i)
36     {
37         inv[i]=qmod(f[i],mod-2);
38         for(int j=i,k=1;j<=1e6;j+=i,k++)
39         if(miu[k])
40         {
41             if(miu[k]==-1)
42             g[j]=1ll*g[j]*inv[i]%mod;
43             else
44             g[j]=1ll*g[j]*f[i]%mod;
45         }
46         g[i]=1ll*g[i]*g[i-1]%mod;
47     }
48     return;
49 }
50 int main()
51 {
52     init();int T;
53     scanf("%d",&T);
54     for(int k=1;k<=T;++k)
55     {    
56         scanf("%d%d",&n,&m);
57         if(n>m)swap(n,m);int ans=1;
58         for(int i=1,j;i<=n;i=j+1)
59         {
60             j=min(n/(n/i),m/(m/i));
61             ans=1ll*ans*qmod(1ll*g[j]*qmod(g[i-1],mod-2)%mod,1ll*(n/i)*(m/i))%mod;
62         }
63         printf("%d\n",(ans+mod)%mod);
64     }
65     return 0;
66 }

 

posted @ 2018-03-23 11:47  大奕哥&VANE  阅读(226)  评论(0)  编辑  收藏  举报