GAT入门
GAT入门(Graph Attention Networks)
1.聊点基础
① 图的两种“特征”
- 对于任意顶点,其和邻居构成第一种特征,即图的结构关系
- 每个顶点都有自己的特征,即GCN中提到的图信号,它可以是社交网络中每个用户个体属性,每个蛋白质的性质等
- 进行图神经网络无外乎就是学习以上的两种特征
②GCN的局限
- 无法处理动态图问题,在GCN中,图的固定邻居矩阵和图信号作为GCN层的输入,这两者一般是固定不变的,而动态图中频繁更新图邻居矩阵会带来巨大的计算和设计难度
- 无法处理有向图,在上一节GCN中,我们默认是在无向图(邻居矩阵为实对称阵)的前提下进行讨论的
- 在GCN中,聚合是统一的,没有区分入度和出度
- 而有向图中入度和出度往往具有不同的含义,比如论文中的引用和被引用,社交网络中的的关注和被关注,而GCN将二者一视同仁,无法表示方向的差异 - (每个邻居被赋予相同的重要性,这不合理!)
③GAT的两种运算方式
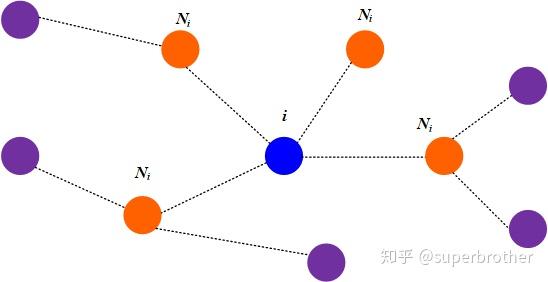
- Global graph attention:对每一个顶点都对图上的任意顶点进行attention计算,即下图中蓝色节点对全部节点都进行注意力计算
- 这种方式不依赖图结构(因为对所有节点都进行一次计算),本质上是对所有点的全局建模,理论上有更强的表达能力
- 但图本身是有结构的,如果不利于的图结构,相当于自废武功,且每轮对所有节点计算时,产生的计算开销极大
- Mask graph attention:注意力机制的计算只在邻居节点上进行,即下图蓝色节点仅对橙色节点进行注意力计算
-
对比Attention is all your need的Mask
- Transformer的Mask控制注意力计算是否允许访问某些位置,这和GAT的Mask类似,GAT的Mask使当前节点只计算其邻居节点的注意力,也算是一种只允许访问某些位置
- GAT的Mask就像给注意力加了“地图”,明确告诉当前节点,哪些边是连通的,哪些是不连通的
- Transformer的Mask主要是控制当前时刻不能访问其他时刻的信息
-
以下的内容均在Mask graph Attention的前提下讨论
2.GAT原理
-
核心思想:邻居特征的重要性可以通过注意力机制自适应学习
-
和Transformer一样,GAT的计算也分“计算注意力系数”和“加权求和”两步骤
①计算注意力系数
-
首先对所有节点做一层共享(参数)的线性变换$h_i^{(1)} = Wh_i$
-
这里的目的将原始节点特征映射到一个更适合做注意力的空间(增维)
-
类似Transformer的QKV映射:对于输入X,分别乘上不同的权重矩阵得到QKV三个矩阵,这里扩展回顾一下Transformer的QKV
- 一方面是将输入特征映射到注意力交互空间
- 另一方面提供更多的灵活性和表达能力:如果直接在输入特征上做注意力,表达能力有限,加入QK映射后,可以为不同的关注方向建模不同的子空间,相当于告诉模型,你在提问(Q)和被提问(K)时的语义可以不同
-
GAT的注意力是所有节点先做一个统一的线性变换,再通过一个共享的注意力网络打分
-
-
计算节点i和j之间的注意力系数
-
$e_{ij} = LeakyReLU(\vec{\alpha ^T}[Wh_i || Wh_j])$
- 首先$[Wh_i || Wh_j]$将顶点i,j变换后的特征进行拼接
- $\alpha$将拼接后的高维特征映射到一个实数上,这个过程和Transformer一样,使用单层前馈神经网络实现,之后加一层非线性
-
之后归一化(转换为概率(0,1))懒得敲了直接上图吧
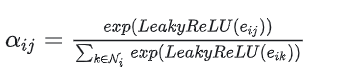
-
最后得到的$\alpha_{ij}$即对于节点i而言,其邻居j的重要程度,一个节点进行注意力系数计算后,就可以知道它的所有邻居中,哪些比较重要,哪些比较不重要,这样的作用就是,每个节点可以根据邻居的重要程度进行动态加权邻居的特征,而不是像之前的平均或加权求和
-
②加权求和
- 即根据计算好的注意力系数,把特征加和求权一下
- $h_i' = \sigma(\sum_{j\in N_i}\alpha_{ij}Wh_j) $ ,输出一个节点特征$h_i$,经GAT后,输出节点新的特征$h'_i$
- 和Transformer一样,引入多头注意力效果更好
3.代码实战
import torch
import torch.nn.functional as F
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import GATConv
#加载数据集
dataset = Planetoid(root='D:/tmp/Cora', name='Cora')
data = dataset[0]
#定义GAT
class GAT(torch.nn.Module):
def __init__(self,in_channels,hidden_channels,out_channels):
super().__init__()
self.gat1 = GATConv(in_channels,hidden_channels,heads = 8,dropout = 0.6) #8个注意力头并行计算
self.gat2 = GATConv(hidden_channels * 8,out_channels,heads = 1,concat = False,dropout = 0.6) #concat = True:将各头的输出在特征维度上拼接,False为将各头的输出取平均
def forward(self,data):
x,edge_index = data.x,data.edge_index
x = F.dropout(x,p = 0.6,training = self.training)
x = F.elu(self.gat1(x,edge_index))
x = F.dropout(x, p=0.6, training=self.training)
x = self.gat2(x, edge_index)
return F.log_softmax(x, dim=1)
#初始化模型和优化器
model = GAT(dataset.num_node_features,8,dataset.num_classes)
optimizer = torch.optim.Adam(model.parameters(),lr = 0.005,weight_decay = 5e-4)
#训练过程
def train():
model.train()
optimizer.zero_grad()
out = model(data)
loss = F.nll_loss(out[data.train_mask],data.y[data.train_mask])
loss.backward()
optimizer.step()
return loss.item()
#测试过程
def test():
model.eval()
logits = model(data)
accs = []
for mask in [data.train_mask, data.val_mask, data.test_mask]:
pred = logits[mask].argmax(dim=1)
acc = (pred == data.y[mask]).sum().item() / mask.sum().item()
accs.append(acc)
return accs
# 跑训练
for epoch in range(1, 201):
loss = train()
train_acc, val_acc, test_acc = test()
if epoch % 20 == 0:
print(f'Epoch {epoch:03d}, Loss: {loss:.4f}, Train: {train_acc:.4f}, Val: {val_acc:.4f}, Test: {test_acc:.4f}')






 浙公网安备 33010602011771号
浙公网安备 33010602011771号