强化学习算法
强化学习算法
1.概述
- 之前入门了强化学习基本术语及MDP,而强化学习相关算法就目前了解,分为在MDP框架下的算法,以及跳出MDP框架下的算法,我们现针对在MDP框架下的算法去学习,先不管跳出MDP框架下的算法。
- 而在MDP框架下,算法又可以分为两大类:基于模型的(model-based)和无模型的(model-free),在这两类之下,又可以按是否使用值函数、是否直接优化策略而进一步分类
- 基于模型:知道环境的状态转移概率$P(s'|s,a)$和奖励函数$R(S,a)$,使用时先建模环境,之后用规划算法寻找最优策略
- 无模型:不依赖对环境的建模,直接通过与环境交互学习(环境是未知的),比如Q-learning
- 使用值函数:学习一个值函数再从中导出策略(比如导出值最大的策略),不直接优化策略,而是通过值函数隐式决定行为,学习过程中不存在一个显示的策略,比如Q-learning
- 直接优化策略:直接学习或优化策略,最大化期望奖励,比如PPO,DDPG
2.Q-learning
- RL入门篇的MDP中策略提取部分,就是在一个已知环境,根据贝尔曼方程,计算出最优的状态价值V(s),再推导出最优策略,这是动态规划的方法,前提是我们知道环境的所有信息(状态、动作、转移概率)
- Q-learning 的目标是学习一个“评分表”(称为 Q-table),告诉你在某个特定位置(状态 s)选择某个特定方向(动作 a) 最终能获得多少总分(累积奖励)。这个分数就是 Q 值,记为Q(s,a)
- Q-learning 是在MDP框架下提出的一种强化学习算法
- 引入RL的核心思想:在未知环境下智能体通过交互学会最优策略,Q-learning是一种无模型基于值的强化学习算法
$$
Q(s_t,a_t)\leftarrow Q(s_t,a_t) + \alpha[r_{t+1} + \gamma \cdot \max_{a’}(Q(S_{t+1},a^‘) - Q(s_t,a_t)) ]
$$
-
上述为核心公式,其中Q(s,a) :在状态s下采取动作a取得的回报 | α:学习率 | $r_{t+1}$:在时刻t执行动作a后的即时奖励 | $\gamma$:衰减因子
-
公式含义:通过对当前Q值进行更新,使当前Q值向目标值靠近
- 目标值:贝尔曼方程计算得出,即当前动作带来的即时奖励$r_{t+1}$ + 下一状态得到的最大期望未来回报,即$\gamma \cdot \max_{a’}(Q(S_{t+1},a^‘)$
- 理解:当前的Q值可能是猜的,或者是初始化值(因为qlearning是在未知环境下),而目标值是看到了奖励+猜测下一状态的最大收益
-
学习的过程 - 学习是如何进行的
-
每次选择动作 - 探索 or 利用
- 探索:随机选择一个动作执行
- 利用:选择当前Q值最大的动作
-
如何更新Q值
- 目标值怎么来
- 在一次次尝试中得到即时奖励r和下一个状态s'
- 从已有的Q表中查s'的最大Q值(初始可能为0),这个值就作为目标值,用于更新当前的Q
- Q值更新
- 有了目标值,更新Q值的过程就是从当前值往目标值靠,即$Q_{s_t,a_t} \leftarrow Q_{s_t,a_t} + \alpha \cdot(目标值 - 当前估计)$
best_next_q = max([Q.get((next_state,a),0.0)for a in env.get_actions()]) current_q = Q.get((state,action),0.0) Q[state,action] = current_q + alpha * (reward + gamma * best_next_q - current_q) - 目标值怎么来
-
-
代码实现:初始化一个Q表,每个元素是一个键值对,key为(state,action),Value为Q值,设定一个训练轮数episodes开始训练,每轮训练都是从起点开始,重复执行:有10%的概率“探索”,即随机选择一个动作,然后执行,更新状态和q值,有90%的概率执行“利用”,即选择当前状态下可获得最大q值的动作,然后执行,更新状态和q值,直到到达终点,结束本轮训练。
#Q-learning
#episodes:训练总回合数,epsilon:探索率,智能体随机选择动作的概率,0.1即10%的时间随机探索,90%的时间利用已知信息
def q_learning(env,episodes = 500,alpha = 0.1, gamma = 0.9, epsilon = 0.1):
#Q-table 存储了在特定状态(state)下执行特定动作(action)的预期未来总回报(Q值)
Q = {} #Q表初始化,key:(state,action),value:Q值
for ep in range(episodes):
state = env.reset()
while (1):
if (np.random.rand() < epsilon):
action = np.random.choice(env.get_actions()) #探索(10%的时间) - 随机选择一个动作
else:
q_vals = [Q.get((state,a),0.0) for a in env.get_actions()]
action = env.get_actions()[np.argmax(q_vals)] #利用 - 选择Q值最大的动作
#执行动作
next_state,reward,done = env.step(state,action)
#更细Q值
best_next_q = max([Q.get((next_state,a),0.0)for a in env.get_actions()])#查找在next_state下哪个动作最佳 - 用于以后的“利用”
current_q = Q.get((state,action),0.0)
Q[state,action] = current_q + alpha * (reward + gamma * best_next_q - current_q) #qlearning公式
state = next_state
if done:
break #停止当前轮循环,开启下一轮,相当于一个训练的过程
return Q
- 也可以将q表打印出来
def print_q_table(Q, env):
data = []
for x in range(env.size):
for y in range(env.size):
state = (x, y)
row = {'state': state}
for action in env.get_actions():
row[action] = round(Q.get((state, action), 0.0), 2)
data.append(row)
df = pd.DataFrame(data)
print("\n📋 Q 表(每个状态对应的动作 Q 值):")
print(df.to_string(index=False))
Q = q_learning(env)
print_q_table(Q, env)
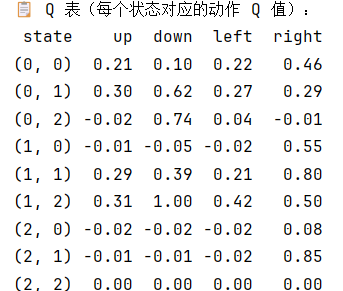
- 应用Q-learning
#从训练后的Q表中提取最优策略
def extract_policy_from_q(Q,env):
policy = {}
for x in range(env.size):
for y in range(env.size):
state = (x,y)
if state == env.goal:
continue
q_vals = [Q.get((state,a),0.0) for a in env.get_actions()]
best_action = env.get_actions()[np.argmax(q_vals)]
policy[state] = best_action
return policy #policy是一个二维矩阵
#agent使用qlearning
def run_agent_with_q(env,policy):
state = env.reset()
env.render()
steps = 0
while state != env.goal:
action = policy[state]
state,reward,done = env.step(state,action)
env.render()
steps += 1
if done:
print(f"到终点辣,用了 {steps}步")
break
if __name__ == "__main__":
env = GridWorld()
Q = q_learning(env) #得到训练后的Q表
policy = extract_policy_from_q(Q,env)
run_agent_with_q(env,policy)
3.策略梯度算法
①概述
- 前面的Q-learning是使用值函数的算法,即在学习过程中不体现策略,而是通过值间接影响策略
- 基于策略的方法首先要将策略参数化,
PPO
- PPO(Proximal Policy Optimization):近端策略优化






 浙公网安备 33010602011771号
浙公网安备 33010602011771号