GCN入门
GCN入门
信息来源
1.基本概念
-
图像与图的差异
- 图像中,每个像素都有固定的位置,都有上下左右四个邻居,一个卷积核在图像的每一个位置都可以做同一件事
- 图结构中,节点之间的连接关系是不规则的,不能在图上“平移"一个卷积核,所以不能用传统CNN的方式在图上提取特征
-
CNN三大特性:参数共享、局部连接性、层次化表达
- 参数共享
- CNN的卷积核在整个图像复用,即同一组权重在不同位置滑动,使用的都是同一参数
- 避免每个位置都学一个参数(梯度爆炸)
- 参数共享的可行性:图像的局部特征具有“平移不变性“,即某种模式(边缘、角点、纹理)在图像的不同位置都可能出现,所以一套参数可以用在不同位置上,因为我们期望图像在不同位置可能包含相同类型的特征
- 局部连接性
- 同一个卷积核,反复作用在图像的不同小块上,输出一个个局部响应
- 局部连接的可行性:不需要全图信息就可以识别出边缘、角点、纹理这些局部特征
- 参数更少,能够提取局部特征,计算效率高,适合处理图像
- 层次化表达
- CNN的浅层学低级特征,深层学高级特征
- 为什么会有层次化:CNN的每一层只看输入的一小部分,捕捉小图案,多层卷积层连续使用,就逐步从小图案拼成完整图像
- 参数共享
-
GCN传播公式$H^{(l+1)} = \sigma(\tilde{D{-\frac{1}{2}}}\tilde{A}\tilde{D{2}}}H{(l)}W)$
- $\tilde{A} = A + I$,其中A为图的邻接矩阵,I为单位阵,$\tilde{A}$即在A的基础上,为每个节点加一个自环边,表示每个节点除了考虑其邻居节点的信息,还会考虑自身的信息
- $\tilde{D}$为$\tilde{A}$的度矩阵,度矩阵(i,i)的位置表示第i个节点的度,其余位置均为0,是个对角阵,度矩阵就是邻接矩阵各行求和,将每行的和放在对角线的位置
- 对角阵的$-\frac{1}{2}$次方即对角元素求对应次方
- $H^{(l)}$为第$l$层所有节点的特征表示
- $W^{{l}}$为第$l$层需要学习的参数
- $\tilde{A}H^{l}$相乘表示每个节点自身及其邻居节点在第$l$层的特征聚合起来,得到一个包含了节点及其邻居特征的新表示
- $\tilde{D^{-\frac{1}{2}}}$对度矩阵进行归一化,因为不同节点的度可能差别很大,若不进行归一化,度大的节点在传播中可能会占据主导地位,导致模型偏向于这些节点,归一化使不同节点的信息传播更加均衡
- 乘以权重矩阵W:对经过邻居信息聚合和归一化处理后的特征进行线性变换,将其映射到一个新的特征空间(维度)中,最外层$\sigma$是非线性激活
-
要搞明白GCN这个公式的来头,GCN的数学原理,需要两部分基础,即谱图理论和傅里叶变换
2.谱图理论入门
①相关基础
-
用线性代数研究图的性质,对图矩阵特征值和特征向量的研究,即谱图理论,eg一个图也可以有特征值
-
特征值 & 特征向量:对于矩阵A,存在非零向量x,若$Ax = \lambda x$,则$\lambda$为A的特征值,x为对应特征值$\lambda$的特征向量
-
标准谱图理论默认是在无向图、邻接矩阵为实对称矩阵的前提下进行讨论的
-
实对称矩阵
-
可相似对角化 - 存在矩阵P,使$P^{-1}AP = P^{T}AP = \Lambda$,即存在矩阵P,可以将矩阵A表示为$A = P\Lambda P^{T}$的形式
-
实对称矩阵不同特征值对应的特征向量相互正交,P是由特征向量拼成的矩阵,所以$PP^{T} = E$
-
-
半正定矩阵:矩阵的特征值>= 0
-
二次型:对于实对称矩阵A,列向量$x$,$F(x) = x^{T}Ax$,即为矩阵A的二次型,若二次型>=0,则该矩阵为半正定矩阵
-
瑞利商(Rayleigh quotient):对于矩阵A,其瑞利商$R(A,x) = \frac{x{T}AX}{XX}$,即矩阵的二次型 / 向量x的模长,若x是A的一个特征向量,则$R(A,x) = \frac{X^{T}\lambda X}{X^{T}X} = \lambda$,即当$x$为特征向量时,矩阵A的瑞利商 = 特征向量$x$对应的特征值
②图拉普拉斯矩阵 & 归一化拉普拉斯矩阵
- 图拉普拉斯矩阵(Graph Laplacian):$L = D - A$,其中A为邻接矩阵,D为度矩阵,因讨论的是无向简单图,因此A是对称阵,而D是对角阵,因此D - A为实对称阵,可相似对角化
- 归一化拉普拉斯矩阵:$L_{sym} = D{-\frac{1}{2}}LD{2}}$
- 归一化是什么,以及为什么要归一化
- 归一化:消除不同数据在“大小”或“尺度”上的差异,使它们更公平,更可比较
- 图归一化的原因:存在度数很大的节点,在传播时其接收邻居聚合的信息就会很大
- 比如节点A有100个邻居,节点B只有2个邻居,在传播时,节点A会收到100个节点的信息,节点B只会收到2个节点的信息,那么节点A的更新量是节点B的50倍,可能导致模型学习不稳定、节点特征消失or爆炸
- 归一化后:稀释节点A邻居的贡献,仍收到100个邻居的信息聚合,但每个邻居的影响被稀释;邻居越多,被稀释的就越多,所以邻居少时,每个邻居都很重要,邻居多时,各邻居的影响平均化
- $L_{sym} = D{-\frac{1}{2}}LD{2}}$称为对称归一化,两侧乘可以保持其实对称性,为了便于理解,我们先看单侧归一化,假设$L' = D^{-1}L = \frac{A_{ij}}{d_i}$,即L的各元素(节点)除以自己的度数,对于节点i,每个邻居j收到的权重是$\frac{1}{d_i}$,这就相当于做了均值聚合
- 图拉普拉斯矩阵和归一化拉普拉斯矩阵均为半正定矩阵,证明如下
- 思路:证明对任意向量$x$,均有其瑞利商>=0,则当$x$为矩阵特征向量时,矩阵瑞利商位特征值$\lambda >= 0$,即可证矩阵为半正定
- $R(A,x) = \frac{x{T}AX}{XX}$,可知分母为向量$x$模长恒>0,所以只需证明分子>=0即可
- 图拉普拉斯矩阵的二次型:度矩阵为对角阵,二次型为标准型(无混合项)

- 从上面得知,L的二次型为$\sum_{i,j}(x_{i} - x_{j})2$,即对任意向量x,都有$xLx>=0$,故当$x$为特征向量时,瑞利商 = $\lambda$大于等于0,故L为半正定矩阵
- 同理可证归一化拉普拉斯矩阵也是半正定矩阵,这里看的头疼,先放一下

- 此外还能证明$L_{sym}$的特征值<=2,即$\lambda$∈[0,2],证明方法先不看了,以后需要看https://www.bilibili.com/video/BV1Vw411R7Fj?spm_id_from=333.788.videopod.episodes&vd_source=ef7dc76f807d26d86d33be41cf55ea77&p=2
3.傅里叶变换
- 干了什么:把信号拆成“频率成分”
- 比如一段音频函数f(x),这个函数可以看做多个正弦波(不同频率、振幅的正弦波)加起来,傅里叶变换就是将原来的波形f(x)(时域)拆成很多正弦波(频域),再比如一段钢琴音,假设由1个440Hz的音,一点880Hz的音和一点1760Hz的音构成,傅里叶变换就是告诉你这个复杂的声音信号,含有哪些频率,每个频率有多少量,以下图为例,傅里叶变换前的视图就相当于从左向右看,只能看到一个函数图像,傅里叶变换后的视图就相当于从右往左看,可以看到音频的“频率成分”
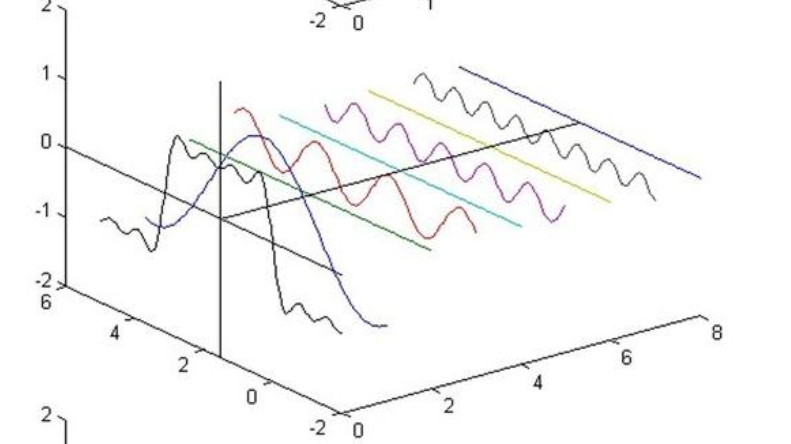
- 下图展示了每个正弦波在不同频率中的振幅是怎样的
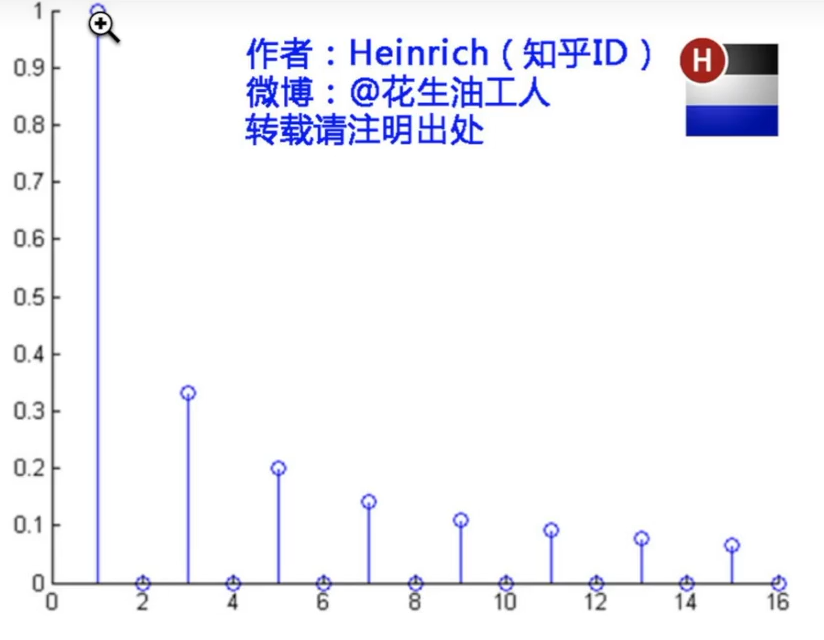
-
频域和时域
- 时域:观察信号随时间变化的方式,比如声音的音频,随时间变化
- 频域:把信号转换为各个频率成分的组合,即我们不看”它在某时刻是怎样的“,而是看”它是哪些频率的波组合而成的“,比如一首钢琴曲包含哪些频率的音调,各自的强度是怎样的
- 傅里叶变换就是将时域->频域,反傅里叶变换就是将频域->时域,傅里叶变换及其逆变换是信息无损的,即傅里叶变换是一个事物在不同域的不同表现,事物本身没有发生任何的改变
- 既然事物本身没有改变,那为什么要做傅里叶变换:因为有些问题在频域里会好处理一些,比如男女生的音频,女生的音频一般要比男生要高,使用傅里叶变换会很显然的将男女生的音频分开处理
-
连续和离散
- 连续的傅里叶变换处理的是连续时间信号,比如模拟音频信号,模拟电压信号
- 离散的傅里叶变换处理的是离散时间信号,信号仅在离散的时间点上有定义,通常是对连续时间信号采样得到,比如数字信号
- GCN中涉及离散的傅里叶变换,以下将离散的傅里叶变换简单入门一下
-
傅里叶变换$\hat{x}k = \sum^{N - 1} x_n \cdot e^{-2\pi i \cdot kn/N}, \quad k = 0, 1, \ldots, N - 1 $
- 即对一个长度为N的离散信号$x=[x_0,x_1,...,x_{N-1}]$(时域形式),目标是将其变为$\hat{x}= [\hat{x}_0, \hat{x}1, \ldots, \hat{x}]$(频域),每一个$\hat{x_k}$是一个频率为k的正弦波在这段信号中的强度(强度:就是频率为k的正弦波,在原信号中参与多少、贡献多大,它是个复数,实部表示大小,虚部表示相位)
- $e^{-2\pi i \cdot kn/N}$是一个复数形式、频率为k的正弦波,怎么来的和欧拉公式有点关系,先不管了,往下看
- $x_n$乘以这个波形,再求和就相当于投影
- 就类似于一个力可以分解为x方向的力和y方向的力
- 波形也可以分解为频率为k的各个分量
-
图上的傅里叶变换
- 为什么图卷积前需要做傅里叶,就是图与图像的不同点
图像中,每个像素都有固定的位置,都有上下左右四个邻居,一个卷积核在图像的每一个位置都可以做同一件事
图结构中,节点之间的连接关系是不规则的,不能在图上“平移"一个卷积核,所以不能用传统CNN的方式在图上提取特征
- 所以在空间域中做不了图卷积,我们借助傅里叶变换将图从空间域变换到另一个域,再进行卷积,最后再借助逆变换将图变回空间域,完成卷积操作(因为傅里叶变换与逆变换是无损的,图本身没有被改变)
4.GCN
①Lx的意义(傅里叶变换+卷积+逆变换)
-
L为上文提到的拉普拉斯矩阵,x为图信号(图上每个节点对应的一个值,比如社交网络中用户的活跃度,交通网络中路口的车流量)
-
Lx表示节点i与其所有邻居差值的求和,以图①-②-③为例
-
简单写就是如下的形式
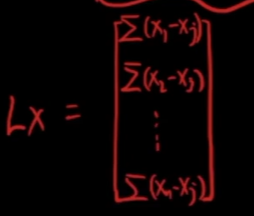
- 由上文可知L可相似对角化,$Lx = U\Lambda U^{T}x$,其中U为L的特征向量拼成的矩阵,为正交阵,$U\Lambda U^T$也为正交阵,下面逐步分解此式
- $U^T x$:对x做了一个正交变换,将x在L的特征向量(的坐标系下)重新表示 ,相当于一步傅里叶变换,新的坐标系相当于图的频域
- $\Lambda U^T x$:每个频率分量(特征向量)乘以特征值,相当于做一个频率滤波,这一步就是CNN的求卷积和的操作
- 最后再左乘U,相当于傅里叶逆变换,将图变换回原来的坐标系
②GCN公式数学推导
公式镇楼:$H^{(l+1)} = \sigma(\tilde{D{-\frac{1}{2}}}\tilde{A}\tilde{D{2}}}H{(l)}W)$
1)谱图卷积定义(频域)
- 图卷积在频域下的定义:$g^*\theta x = Ug\theta(\Lambda)U^T x$,即上文的Lx
- 这个式子的问题:计算U需要求特征值和特征向量,如果图很大的话计算量难以想象,$g_\theta(\Lambda)$是一个关于$\Lambda$的多项式,当图很大时,会有梯度消失/爆炸的问题,所以引出下面的切比雪夫多项式
2)切比雪夫多项式近似卷积核(频域核$g_\theta(\Lambda)$)
- 切比雪夫多项式:$T_n(x) = 2xT_{n-1}(x)-T_{n-2}(x$),即为一个递推式,其中$T_0 = 1,T_1 = x$
- 为什么切比雪夫多项式不会有梯度消失/爆炸的问题:其性质$T_n(cos\theta)=cos(n\theta)$,即不论n多大,多项式都在[-1,1]之间
- 但上式需要$g_\theta(\Lambda)$的$\Lambda$在[-1,1]之间,即特征值在[-1,1]之间;在谱图理论中我们说过,$L_{sym}$的特征值在[0,2]之间,所以构造$L_{sym} - I$,其特征值在[-1 ,1]之间,其中$I$为单位阵
- 所以卷积的定义可以写为$g^*\theta x = U(\sum^{k}\theta _kT_k(\Lambda))U^T x$,其中$\theta _k$为每个位置学习的参数
- 进一步推导
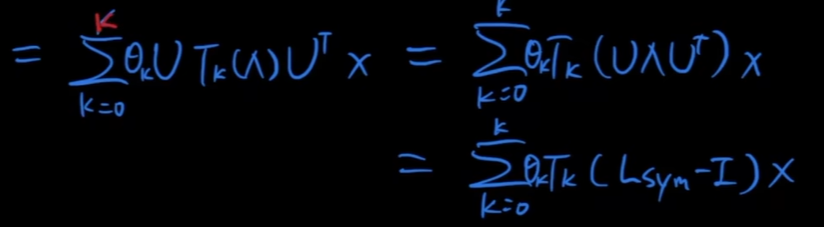
- 切比雪夫的问题:计算$T_k$时需要对矩阵求k次方,计算量还是很大,所以进行一阶近似
3)一阶近似估计
- 即只让$T_k$计算到一阶,二阶及以上都忽略
- 则$\sum_{k=0}^{K}\theta_kT_k(L_{sym}-I)x = \theta_0T_0(L_{sym}-I)x + \theta_1T_1(L_{sym}-I)x$,再代入$T_0 = 1,T_1 = x$,注意Lsym - I是自变量,不是乘积(●'◡'●),原式$=\theta_0x + \theta_1(L_{sym}-I)x$
- 而$L_{sym} = D{-\frac{1}{2}}LD{2}} = D{-\frac{1}{2}}(D-A)D{2}} = I-D{-\frac{1}{2}}AD{2}} $
- 故原式$g^*_\theta x=\theta_0x-\theta_1D{-\frac{1}{2}}AD{2}}x$
4)将两个参数合并为一个权重矩阵
- 令$\theta_1 = -\theta_0$,原式$=\theta_0(I + D{-\frac{1}{2}}AD{2}})x$
5)简化参数 + 自连接
- 上面的是最初的近似版本,后来他们又提出:与其使用两个参数,不如直接给邻居矩阵A加自环,这样的好处是可以使用一个邻居矩阵A表示节点+邻居,A加自环边即加一个单位阵,$\tilde{A} = A+I$
- 这样只需要一个参数矩阵W
- 原式 $=D̃^{-1/2} (A + I) D̃^{-1/2} xW$
6)扩展到多特征输入
- 即输入X为一个矩阵,每个节点有多个输入特征
- 再加上非线性激活
- 最后$H = \sigma\left( \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} X W \right)$
7)扩展到多层
- 就像多层CNN一样,每一层都有输入和输出
- $H^{(l+1)} = \sigma(\tilde{D{-\frac{1}{2}}}\tilde{A}\tilde{D{2}}}H{(l)}W)$
想一小步反推方便理解
-
上面主要是正推,即从最内层出发,阐述公式如何一步步到最外层我们看到的那样,下面主要是从最外层的公式出发,想一想GCN接收一个图,如何一步步进行处理,为了便于理解,我们先讨论单层GCN,即$H = \sigma\left( \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} X W \right)$
-
GCN的输入,是一张图,对于图中每个节点的图信号记为X,如果是单特征X为向量,多特征X为矩阵,对于这张图我们也可以得到邻居矩阵A,给A加自环我们可以得到$\tilde{A}$
-
GCN的传播矩阵为$\tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2}$,为了方便我们记为$\hat{A}$,$\hat{A}x$实际上就是我们上面说的$Lx$,也就是傅里叶+卷积+逆傅里叶的操作,这个线性变换看似是在空间域做的,本质上将其变换到谱域中完成的
- 可以有以下推导,也就是前者为传播矩阵在空域的形式,后者为其在谱域中的等价形式,即在谱域中传播矩阵$\hat{A}=I-L_{sym}$
$$
\begin{align}
L_{\text{sym}} &= D^{-1/2}(D - A)D^{-1/2} \
&= I - D^{-1/2} A D^{-1/2} \
\Rightarrow \quad D^{-1/2} A D^{-1/2} &= I - L_{\text{sym}}
\end{align}
$$
③代码实战
- GCN + ReLU + GCN
- 输入5 * 3的矩阵,即5个节点,每个节点的图信号为3维,输入形式即N * F_in
import torch
import torch.nn as nn
import torch.nn.functional as F
class GCNLayer(nn.Module):
def __init__(self,in_features,out_features,bias=True):
super(GCNLayer,self).__init__()
self.linear = nn.Linear(in_features,out_features,bias=bias)
#X为图信号,A为邻接矩阵
def forward(self,X,A):
I = torch.eye(A.size(0),device = A.device) #单位阵 A.size(0)即A的行数
A_hat = A + I
D_hat = torch.diag(torch.pow(A_hat.sum(1),-0.5))#按行求和得到度矩阵,再进行归一化
A_norm = D_hat @ A_hat @ D_hat #对称归一化
#GCN传播
out = A_norm @ X #特征变换,实际上是在谱域进行卷积
out = self.linear(out)
return out
class SimpleGCN(nn.Module):
def __init__(self,in_features,hidden_features,out_features):
super(SimpleGCN,self).__init__()
self.gcn1 = GCNLayer(in_features,hidden_features)
self.gcn2 = GCNLayer(hidden_features,out_features)
def forward(self,X,A):
#第一层
h = self.gcn1(X,A)
h = F.relu(h)
#第二层
h = self.gcn2(h,A)
return h
def example():
#节点个数,每个节点的输入维度,GCN隐层维度,输出类别数
N,F_in,F_h,C = 5,3,4,2
X = torch.randn(N,F_in) #生成一个形状为 [N, F_in] 的随机输入特征矩阵 X
A = torch.tensor([
[0,1,0,0,1],
[1,0,1,0,0],
[0,1,0,1,0],
[0,0,1,0,1],
[1,0,0,1,0]
],dtype = torch.float32)
model = SimpleGCN(F_in,F_h,C)
logits = model(X,A) #logits一般表示模型最后一层输出
print("logits shape:",logits.shape)
print(logits)
if __name__ == "__main__":
example()
- 输出5*2的矩阵,即5个节点,每个节点的图信号为2维,这里就可以看做一个分类问题,节点被分为两个类别
logits shape: torch.Size([5, 2])
tensor([[ 0.4953, -0.3602],
[ 0.5028, -0.3527],
[ 0.5017, -0.3526],
[ 0.4360, -0.3673],
[ 0.4310, -0.3752]], grad_fn=<AddmmBackward0>)






 浙公网安备 33010602011771号
浙公网安备 33010602011771号