GNN入门

图神经网络

1.图概述

①基本概念

• 如何表示图 - 使用向量，以A Gentle Introduction to Graph Neural Networks为例
  • 使用6个维度的向量表示顶点信息
  • 使用8个维度的向量表示边的信息
  • 使用5个维度的向量表示全局信息，全局信息例如节点数、边数、最长路径等
• 有向图与无向图
  • 无向图：双向的关系，例如好友关系
  • 有向图：单向的关系，例如B站的关注关系

②如何使用图(graph)进行建模

• 图表示图像

  • 将图像上的每一个像素都映射到图上的某一个点，比如左上角的像素被映射到(0,0)点
  • 一个点的颜色、亮度通常都会和它周围的点有关系
  • 非边缘的像素点通常由8个邻居（上下左右+四个对角）
  • 使用邻接矩阵表示哪两个点之间有边

  

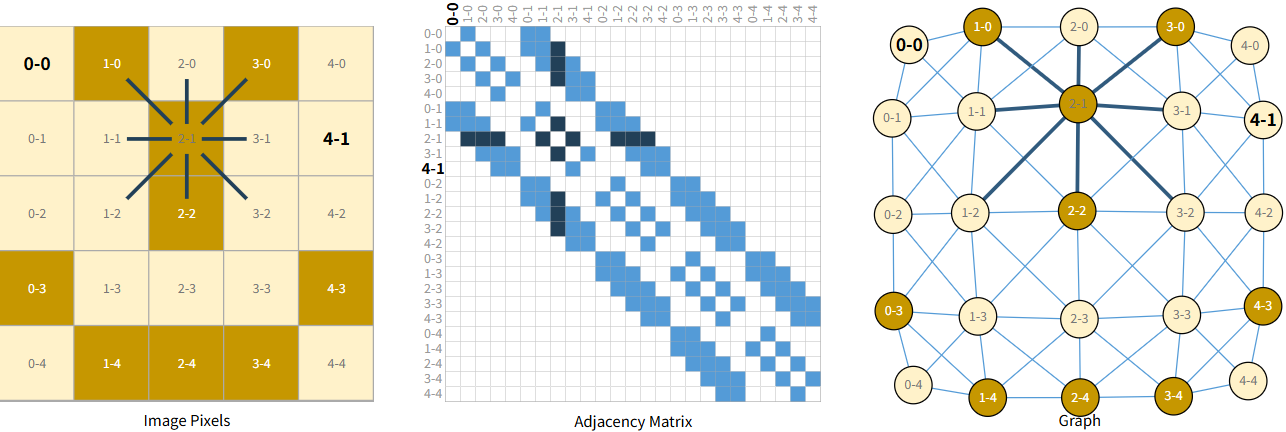
• 图表示文本

  • 每个单词作为一个顶点

  • 边表示单词之间的相邻关系，本例中是单向关系

    

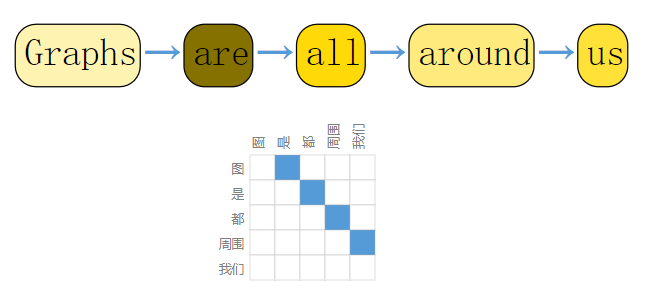
• 社交网络表示成图

  • 将个人表示成节点
  • 将人与人之间的关系表示成边（双向）

  

• 此外还可以将化学中的分子结构、论文中的引文、知识图谱等内容都可以表示成图

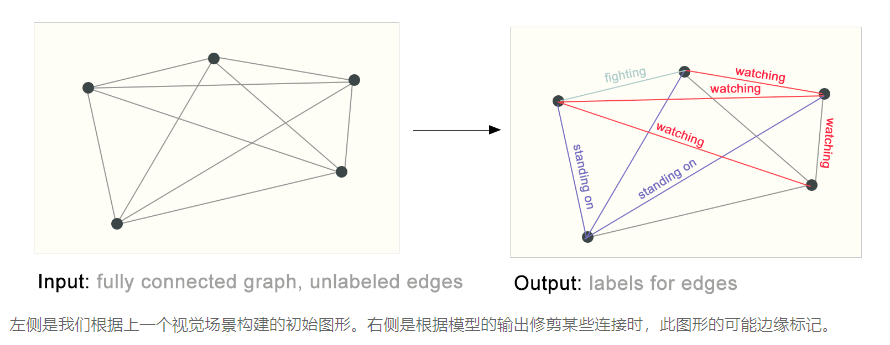
③图结构的相关问题

• 图形级：预测整个图的单个属性，例如预测一个图中是否有环

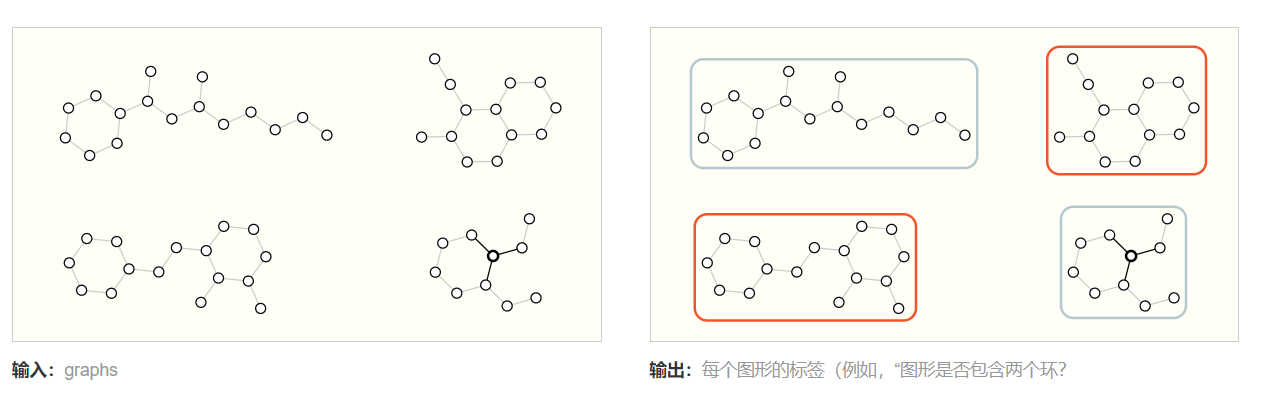
• 顶点级：预测图中每个节点的属性，比如预测某个节点的身份

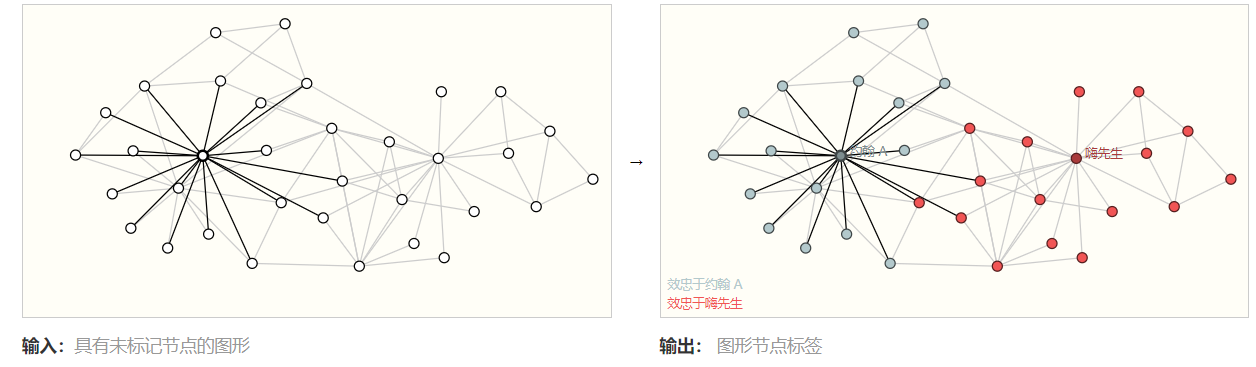
• 边级：预测图中边的属性，例如预测实体之间的关系

2.将图应用于神经网络

①相关问题及解决

• 图包含的4种信息为：节点、边、全局信息、连通性，这些信息将作为输入送到神经网络中
  • 在上文提到前三者都可以使用向量表示
  • 对于连通性：可以使用邻接矩阵表示
    • 如果图很大，其邻接矩阵也很大，且可能会稀疏，在空间上效率很低
    • 一个图交换节点顺序，可能会产生不同形式的邻接矩阵，而这些邻接矩阵表示的都是一个图，有点类似于同构图的感觉
    • 所以通常不使用邻接矩阵表示连通性，而是借助下面的方法
• 使用一个列表表示图的连通性，[1,0]表示顶点1和顶点0有边相连

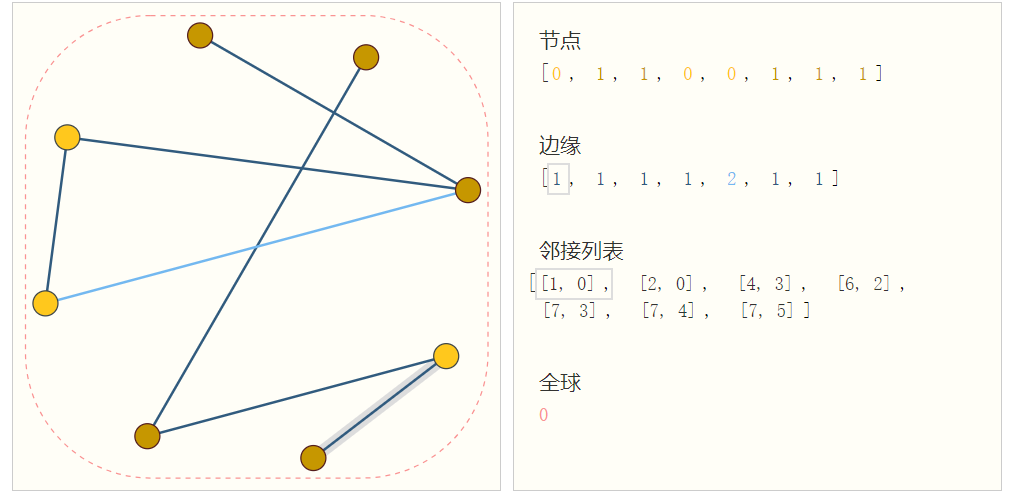
②图神经网络GNN

1)相关概念

• 定义：GNN是图的所有属性（顶点、边、全局属性、连通性）的可优化转换（可训练，可学习参数），它保持图的对称性（节点编号变化不会影响结果），它的变化作用在节点、边、全局属性上
• 图进图出，输出的图同样有节点、边、全局信息，只是特征被更新了，变得更有用了、更难用于后续的任务了

总结：GNN本质上是对节点、边、全局属性进行一种“保持图结构不变”的、可以优化学习的变换，使用消息传递的框架来具体实现这种操作。输入是图，输出也是图，只是图里的特征更新得更好了。

• 消息传递机制

  1. 每个节点将自己的特征（一个向量）发给邻居，类似计网的RIP协议，这个特征可以是自己的特征，也可以是乘个矩阵、加个偏置啥的特征
  2. 一个节点可能会收到多个邻居的消息，需要将这些消息聚合起来，聚合的方法可以是【求和】【取平均】【取最大】
  3. 节点根据聚合好的信息，加上自己的特征，进行特征的更新

  每一轮，节点 = 看自己的邻居，吸收邻居的特征，总结一下，更新自己。

2)构造一个最简单的GNN

• 对图的每一个顶点、边、全局信息套一个小的神经网络（比如MLP - 多层的线性变换 + 激活函数）去更新，例如节点特征->MLP处理->新节点特征，每一类元素用一个MLP，不同元素用不同MLP，同一类内部共享参数。

• 更新一次节点、边、全局这样的小模块称为GNN Layer或GNN Blocks，【注】虽然特征被更新，但图的结构没变，输入和输出都是图，只是特征变了，变得更有用了

  

• 满足分类预测问题：对于最后一层的节点应用线性分类器+Softmax

• 知道边的信息但不知道顶点信息，需要对顶点进行预测，预测方法为：收集边的信息提供给顶点预测，使用池化完成这点

  • 池化分两步，先【收集信息】，比如预测某顶点信息，那首先将与它相关边的信息全拿过来，把这些边的信息排成一个矩阵；
  • 其次把刚才收集到的矩阵进行一个【合并】的动作，比如顶点A收集到信息矩阵，合并的动作可以是将每一列元素进行求和（这里假设顶点和边的向量维度一致，不一样的话还需要进行投影）

• 和CNN池化的关系：二者都是进行聚合操作，但CNN的池化是为了缩小特征图，减小计算量，而GNN这里的池化是为了聚合邻居信息，增强节点表达

• 知道顶点预测边，或知道全局信息预测边or顶点的道理和上面是一样的，下图为一个最简单的GNN，

  

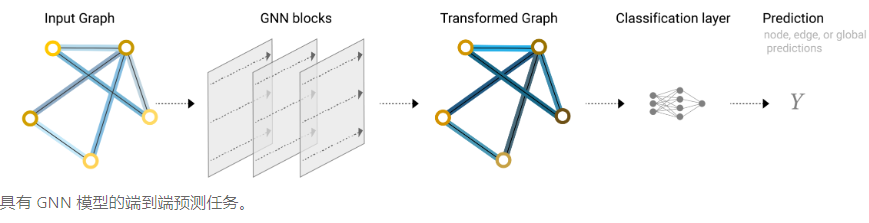
3)在图的各个部分之间传递消息

• 上面的最简单的GNN没有在GNN层内使用图的连通性，比如在做顶点的MLP时，对于单个顶点就是经过一层MLP更新特征后输出，没有考虑到其相连边或顶点的信息

• 消息传递步骤

  1. 对于图中每个节点，收集所有相邻节点的信息，即g函数

  2. 通过聚合函数(sum,avg)聚合所有信息（前两步就是池化的操作）

  3. 所有池化信息通过update更新函数传递

     

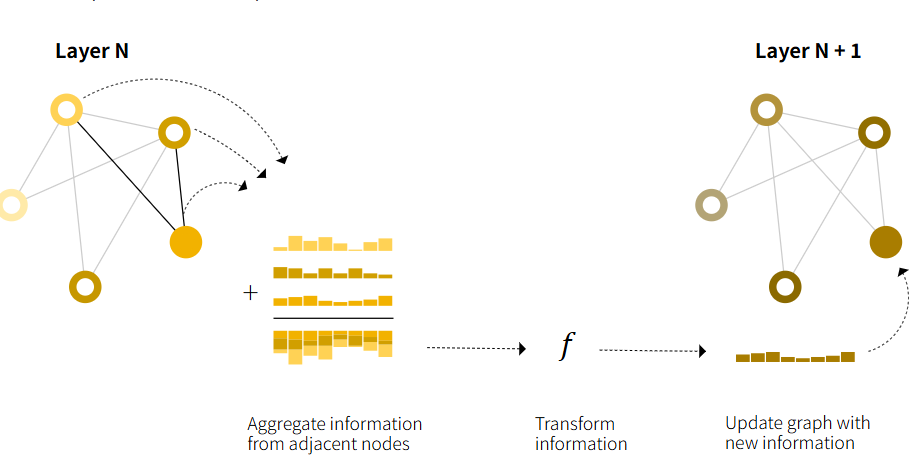
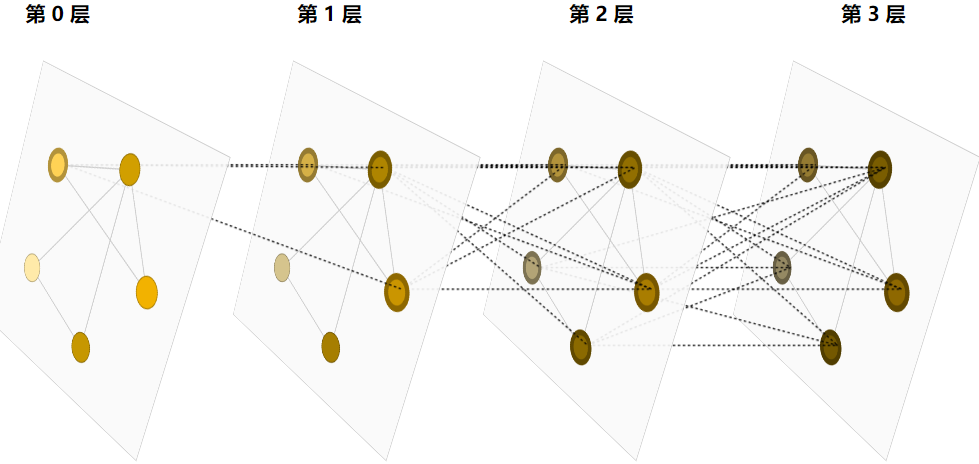
• 通过将传递GNN的消息层堆叠到一起，节点最终可以合并来自整个图的信息，eg在三层之后，节点拥有距离它3步远节点的信息

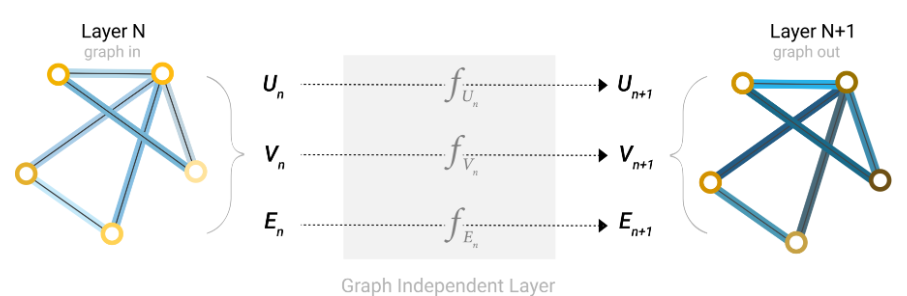
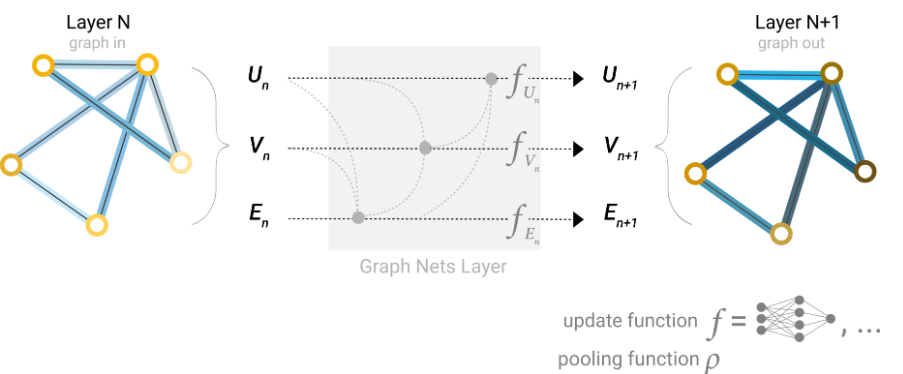
• 下图：顶点、边、全局信息，先通过池化（收集+聚合），再进行update更新，最终得到输出图（layer N+1)

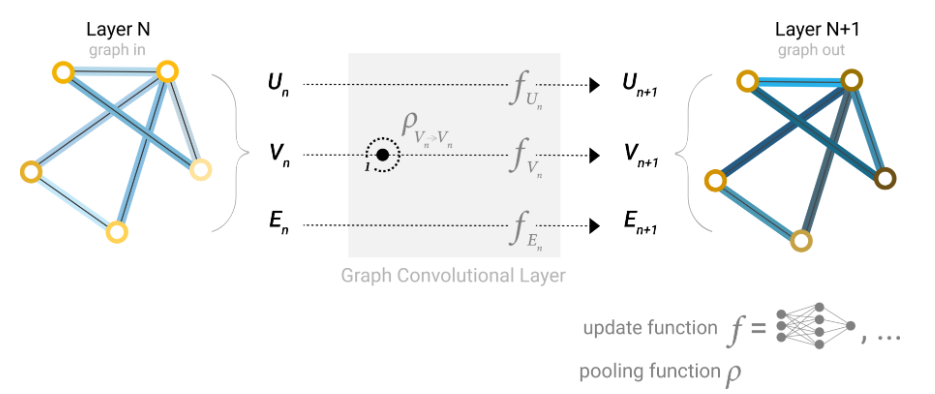
4)将信息传递用于节点/边信息预测

• 上面的知道边预测顶点信息、知道顶点预测边信息都是在最后一步进行的，为了更好的将边的信息给顶点(或是反过来)，我们可以在GNN的每一层都使用消息传递机制，以将相邻边的信息给顶点为例，步骤如下：
  1. 聚合邻边信息
  2. 更新边的信息（使用更新函数）
  3. 将更新后边的特征传递给顶点
• 这样可以使节点和边之间的信息交互变得更流畅，而不仅仅局限于某个阶段
• 更新顺序：是先更新顶点的表示还是先更新边的表示，编织式更新：顶点信息和边的信息交替更新
  • 顶点到顶点：通过线性变换update函数更新顶点信息
  • 边到边：通过线性变换update函数更新边信息
  • 顶点到边：节点的特征可以更新边的信息，即节点的更新结果可以进一步影响边的更新结果
  • 边到顶点：边的特征可以更新顶点的信息，即边的更新结果可以进一步影响顶点的更新结果
• 为什么交替更新有意义：节点和边是相互依赖的，交替更新可以充分利用这种交替更新的关系

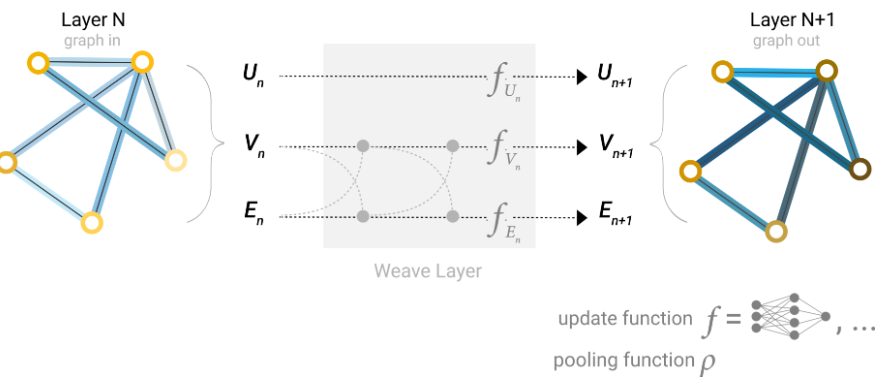
5)利用全局信息

• 上面提到，将传递GNN的消息层堆叠到一起，k层之后，节点就拥有了距离它k步顶点的信息，但如果图过于庞大，顶点之间的距离可能会很长，此时如果想要顶点拥有其他所有顶点的信息，GNN会很复杂，计算成本高
• 一种解决方法是使用全局信息U，又称主节点或上下文向量，主节点连接了图的所有节点和边，可以作为桥梁传递信息
• Eg：顶点的信息收集给边时，也会将U的信息给边，边的信息给顶点时也一样

6)最终预测

• 即模型最后一层，可以仅使用顶点or边的信息做预测，也可以加上全局信息，也可以加上相邻顶点或边的信息，都可以
• （上面的信息都是向量形式），这些不同类别的信息可以加在一起，可以合并在一起，也都可以

7)GNN中的采样图和批处理

• 图采样通过选择子图减小计算量，批处理通过mini-batch实现高效训练

• 传统神经网络通过mini-batch采样，但应用于图上会因为图的不规则性产生问题

  • 图中每个节点的邻居数量不同，连的边数量也不同，无法定义固定大小的批量
  • 如果随机截取子图，可能破坏子图的拓扑性质 - 相邻顶点和边被截出，eg一个分子的子图可能是另一个分子

• 需要解决的问题

  • 采样的子图需要保留原图的关键结构（邻接关系、连通性）
  • 采样方法可以适用于不同场景，eg引文网络、分子图、社交网络

• 待补充

3.图类型扩展

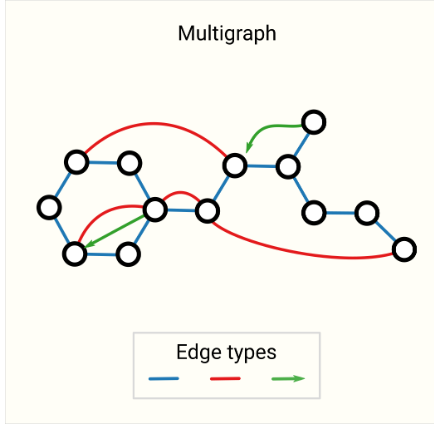
①Multigraphs（多重图）

• 允许两个节点之间有多条边，这些边可以分别是有向的或无向的
• 应用：社交网络中，A和B可以通过多条边沟通（电话、邮件、聊天）

②Hypergraphs（超图）

• 一条边可以连接2个以上的顶点，超图的边类似一个集合，包含多个边
• 应用：协作网络，一个项目小组（超边）可能有多个成员（顶点）

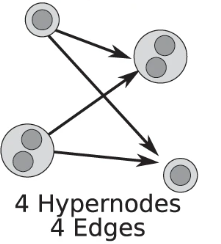
③Hypernodes（超节点）

• 一个节点表示多个对象或子节点，在超图的背景下，超节点通常用于表示一个集合或多个相连的节点
• 应用：节点可能需要表示一个集合，而不是单一的实体

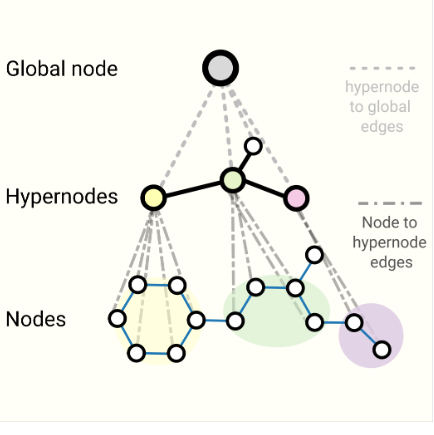
④Hierarchical Graphs（分层图）

• 节点可以分为不同的层级，通常顶层节点表示系统的整体结构，底层节点表示具体的元素
• 应用：公司职级，顶层是CEO；文件系统的目录树，顶层是根目录
• 下图的第二层中节点为超节点