MDP & Q-learning
1.基本概念
- 强化学习讨论的问题:一个智能体(agent)如何在一个复杂的环境(environment)中去极大化它所获得的奖励。通过感知环境的状态(state)对动作(action)的反应(reward),来指导更好的动作,从而获得最大的收益(return)。以上过程称为在交互中学习,这样的学习方法称为强化学习。
- 一个例子:机器人走网格
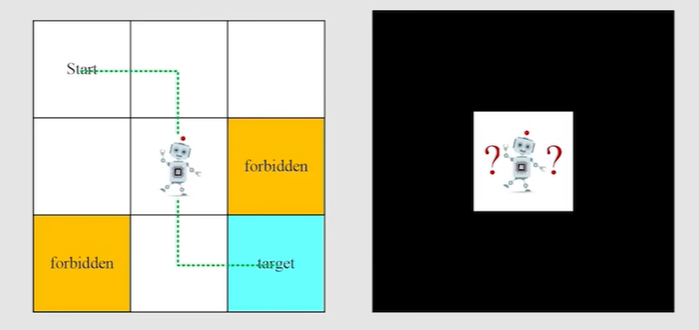
-
state:agent相对于environment的一个status,在上面的例子中,state就是指位置,使用s1-s9表示这些位置状态;环境决定状态
-
state space(状态空间):即所有状态的集合
-
Action:agent在某一时刻根据当前state做出决策/选择的行为,在上面例子中,在一个位置状态下,可能有5个action(向上下左右走&原地不动)
-
离散的动作空间:动作的选择是可数的,比如这里的上下左右,常用算法:Q-learning
- 连续的动作空间:动作类型是一个实数区间(无限可能),比如手臂的力度
-
Action space of state:当前状态下所有的action集合 - 每个状态都有一个action space
-
state transition:agent在某一state下执行某种action,转移到另一个state
- 如果action触碰到边界,则相当于agent原地不动
- 如果action进入到forbidden area,有两种情况:①forbidden area可进入,则直接进入;②forbidden area不可进入,则相当于原地不动

-
state transition probability:借助条件概率去描述状态转移
-
比如当前在s1,执行动作a2后,若P(s2|s1,a2) = 1,则说明一定会到达s2
- 若P(s2|s1,a2) = 0.5,P(s5|s1,a2) = 0.5,则说明有50%的概率到达s2,有50%的概率到达s5
-
policy(策略):根据当前state,决定采取什么action
-
Reward(奖励):环境给agent一个反馈,用来指导agent是不是做得好,比如机器人走到出口 + 1分,机器人撞墙 - 1分
-
Episode(回合):agent从起点出发,直到任务结束,称为一轮
-
Trajectory(轨迹):agent一轮行动中,形如(状态,动作,奖励)这样的序列
-
Return(回报):从当前开始,到终点累计的总奖励(Reward之和),强化学习的目标就是最大化期望的Return,Return可以用来评估Policy的好坏
-
模拟机器人寻路代码
import numpy as np
import time
class GridWorld:
def __init__(self,size = 3):
self.size = size
self.start = (0,0)
self.goal = (self.size - 1,self.size - 1)
self.reset()
def reset(self):
self.state = self.start #回到起点
return self.state
def step(self,action):
x,y = self.state
if action == "up" : x = max(0,x - 1)
elif action == "down" : x = min(self.size - 1,x + 1)
elif action == "left" : y = max(0,y - 1)
elif action == "right" : y = min(self.size - 1,y + 1)
self.state = (x,y)
reward = 1.0 if self.state == self.goal else -0.1
done = self.state == self.goal #判断游戏是否结束
time.sleep(1) # 每步暂停 1 秒
return self.state, reward,done
def get_actions(self):
return ["up","down","left","right"]
def render(self):
grid = [["⬜" for _ in range(self.size)] for _ in range(self.size)] #_仅表示一个占位符,grid是一个二维列表
x,y = self.state
gx,gy = self.goal
grid[gx][gy] = "🏁"
grid[x][y] = "🟩"
for row in grid:
print(" ".join(row)) #" ".join(row) 会把这几个元素用空格 " " 连接成一个字符串
print() #打印一个空行
if __name__ == "__main__":
env = GridWorld()
state = env.reset()
env.render() #生成网格图
for _ in range (20):
action = np.random.choice(env.get_actions())
next_state,reward,done = env.step(action)
print(f"Action:{action},Next state:{next_state},Reward:{reward}")
env.render() #绘制步数之后的网格表
if done:
print("✔️successful pass!")
break
2.马尔科夫决策过程(MDP)
①基本概念
-
为什么需要MDP:强化学习中,agent需要在一个环境中不断做决策,获得奖励,从而学习“好行为”,为了严谨的描述
决策 - 反馈 - 学习的过程,就引入MDP -
MDP是对完全可观测环境进行描述的,观测到的状态内容完整决定了决策的需要的特征
- 你不需要依赖历史信息或者猜测隐藏变量——当前的状态就足够做出合理的动作选择(不关心「怎么来到这个状态」(没有“前序”))
- 例如机器人走迷宫就是完全可观测,不需要知道“你从哪儿来”、“你之前走了几步”——当前状态已经够用了
-
马尔科夫性:未来只依赖于当前状态和当前动作,与过去无关,因为当前的状态就包含了过去的信息
- 使用状态转移概率:$$p_{ss'} = P[S_{t + 1 = s'} | S_t = s]$$描述马尔科夫性,即在当前状态为s的条件下,下一时刻状态转移到s’的概率,这个概率就被称为状态转移概率
- $S_t$为t时刻的状态
- $P_{ss'}$为当前状态为s,下一时刻转移到s‘的概率
- 状态转移矩阵定义了所有状态的转移概率,矩阵中每行元素的和为1
- 使用状态转移概率:$$p_{ss'} = P[S_{t + 1 = s'} | S_t = s]$$描述马尔科夫性,即在当前状态为s的条件下,下一时刻状态转移到s’的概率,这个概率就被称为状态转移概率
$$
\begin{bmatrix}
p_{11} ... p_{1n}\
\vdots \
p_{n1} ... p_{nn}
\end{bmatrix}
$$
-
马尔科夫过程:又称为马尔科夫链,是一个无记忆的随机过程,可以用一个元素<S,P>表示,其中S表示状态集,P表示状态转移矩阵
-
示例:学生马尔科夫链:每个圆圈表示状态,箭头表示在当前状态下转移到目标状态的概率,根据此图不难画出状态转移矩阵
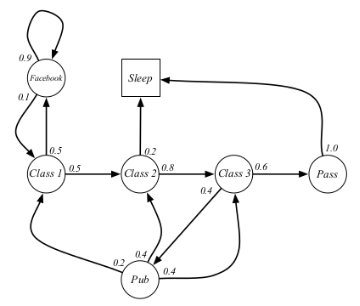
②马尔科夫奖励过程 Markov Reward Process & 回报Return
- 即在马尔科夫过程的基础上,增加了奖励R和衰减系数$\gamma$,故可以用<S,P,R,$\gamma$>表示
- 奖励即当前时刻t在状态s下,在下一个时刻能获得的奖励期望,即$$R_S = E[R_{t+1}|S_t = s]$$
- 衰减系数:是一个[0,1]的数,表示未来奖励的重要程度
- 什么是未来奖励:比如做日结,每天100元,共7天
- 现实生活中,大多人认为今天拿到的钱 > 未来拿到的钱,所以引入了衰减因子,弱化将来的奖励,即越远的奖励,价值越低
- 回报Return:即从当前时刻t开始,到结束所有奖励的总和
联系第一部分的概念
Reward(奖励):环境给agent一个反馈,用来指导agent是不是做得好,比如机器人走到出口 + 1分,机器人撞墙 - 1分
Return(回报):从当前开始,到终点累计的总奖励(Reward之和),强化学习的目标就是最大化期望的Return,Return可以用来评估Policy的好坏
- 未来奖励计算 $$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... \gamma^n R_{n+1}$$
- $\gamma$偏向0,则表明趋向于“近视”性评估
- $\gamma$偏向1,则表明偏重考虑远期的利益
- 可以推导得$G_t = R_{t+1} + \gamma G_{t+1}$(提一个$\gamma$出来)
③价值函数 Value Function
- 价值函数给出某一state或action的长期价值
- 某一状态的价值函数$$v(s) = E[G_t|S_t = s]$$,即从当前状态开始,马尔科夫链收获(Return)的期望(期望能获得的未来所有回报的期望值)
- 当$\gamma$ = 0时,各状态的即时奖励同各状态的价值相同(也就是上面说的近视)
- 当$\gamma$ != 0时,各状态的价值就需要通过计算得到
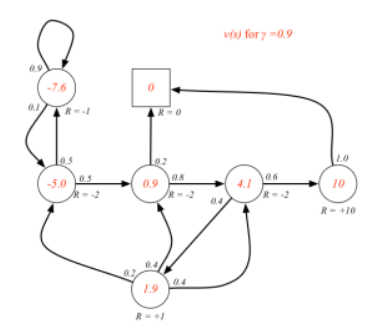
- 上图是$\gamma$ = 0.9的情况,可以简单理解一下,比如状态为class3时,即时奖励R = -2,但因为衰减因子为0.9,因此会偏重考虑远期的利益,而class3有0.6的概率会进入pass,而pass的及时奖励为10,故经计算可得class3的价值为4.1(意思就是因为考虑了远期利益,class3的价值相比即时价值大大增加)
- Return和价值的区别
- Return是对单个Trajectory所求的
- state Value是针对多个Trajectory的Return,求这些Return的期望
④贝尔曼公式
- 尝试对上述的某一状态的价值函数进行化简
$$
\begin{align}
v(s) &= E[G_t|S_t = s]\
&= E[R_{t+1} + \gamma R_{t+2} + \gamma ^2 R_[t+3] +...|S_t = s]\
&= E[R_{t+1} + \gamma(R_{t+2} + \gamma R_{t+3} +...)|S_t = s]\
&= E[R_{t+1} + \gamma G_{t+1}|S_t = s]\
&= E[R_{t+1} + \gamma v(S_{t+1})|S_t = s]
\end{align}
$$
- 前面3行就是递归,重点理解最后一行$G_{t+1} = v(S_{t +1})$,由上述可知
- $G_{t+1} = R_{t+2} + \gamma R_{t+3} + \gamma^2 R_{t+4} + ... \gamma^n R_{n+1}$,表示t+1时刻开始,未来可获得的总奖励,也就是收获Return
- $v(s_{t+1}) = E[G_{t+1}|S_{t+1} = s]$,表示t+1时刻开始,不同trajectory的Return的期望
- 暂且理解:在你还不知道将来会走到哪个状态的时候,就可以用对 $S_{t+1}$ 的期望来近似$G_{t+1}$
- 所以价值函数可以拆解为$$v(s) = E[R_{t+1}|S_t = s] + E[\gamma v(S_{t+1})|S_t = s)]$$
- 前一部分为当前时刻的即时奖励
- 后一部分为下一时刻状态的价值期望
- 因此贝尔曼方程提供了一种递归的方式来计算每个状态的价值
- 价值迭代:基于动态规划,反复应用贝尔曼方程来计算每个状态的最优价值
- 策略评估:给定一个策略,计算每个状态的价值
- 策略改进:在评估策略之后,更新策略为当前状态下选择价值最大的action
- 实现价值迭代:在
GridWorld中计算每个位置的价值并最终得到最优策略。
def value_iteration(env,gamma = 0.9,threshold = 0.01):
value_table = np.zeros((env.size,env.size)) #状态价值表
while (1):
delta = 0
for x in range(env.size):
for y in range(env.size):
state = (x,y)
if state == env.goal:
continue
action_values = [] #动作价值
for action in env.get_actions():
next_state,reward,done = env.step(state,action)
action_value = reward + gamma * value_table[next_state[0],next_state[1]] #贝尔曼公式
action_values.append(action_value)
max_action_value = max(action_values)
delta = max(delta, abs(value_table[x, y] - max_action_value)) #价值更新的差值
value_table[x, y] = max_action_value
if delta < threshold:#如果一次迭代中,所有状态的价值变化都很小(小于 threshold),就认为已经“收敛”了,也就是说差不多已经是最优解了,就可以 停止迭代。
break
return value_table
if __name__ == "__main__":
env = GridWorld()
values = value_iteration(env)
print("最终状态价值表:")
print(np.round(values, 2))
⑤马尔科夫决策过程
-
就是在马尔科夫奖励过程的基础上加一个
decision过程,对比奖励过程多了一个动作集合,使用<S,A,P,R,$\gamma$>来表示- S - 状态空间
- A - 动作空间
- P - 状态转移概率,$P_{ss'}$为当前状态为s,下一时刻转移到s‘的概率
- R - 奖励函数Reward
- $\gamma$ - 衰减因子
-
策略(policy):使用π表示策略的集合,
π(a|s)表示状态为s时,采取行动a的概率 -
目标:找到一个策略π,使得长期累积奖励(Return)最大化 - 即上面的$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... \gamma^n R_{n+1}$
-
策略提取:对每个状态,尝试所有动作,计算最优价值
#提取每个状态的最优动作(即策略)
def extract_policy(value_table,env,gamma = 0.9):
policy = np.full((env.size,env.size)," ",dtype=object) #存储最优策略
for x in range(env.size):
for y in range(env.size):
state = (x,y)
if state == env.goal:
continue
action_values = []
for action in env.get_actions():
next_state,reward,done = env.step(state,action)
action_value = reward + gamma * value_table[next_state[0], next_state[1]]
action_values.append(action_value)
best_action = env.get_actions()[np.argmax(action_values)] #action_values是价值列表,取价值最大的action的序号i,get_actions()[i]对应的动作就是最优动作
policy[x,y] = best_action
return policy
- 可视化 + agent应用最优策略
#打印最优策略
def render_policy(policy, env):
arrow_map = {
"up": "⬆",
"down": "⬇",
"left": "⬅",
"right": "➡",
" ": " " # 空白用于目标状态
}
print("最优策略图:")
for x in range(env.size):
row = ""
for y in range(env.size):
if (x, y) == env.goal:
row += "🏁 "
else:
row += arrow_map[policy[x, y]] + " "
print(row)
#最优策略应用到agent
def run_agent(env,policy):
state = env.reset()
env.render()
steps = 0
while state != env.goal:
action = policy[state]
state, reward, done = env.step(state,action)
env.render()
steps += 1
if done:
print("✔️successful pass!")
break
- 完整代码
import numpy as np
import time
class GridWorld:
def __init__(self,size = 3):
self.size = size
self.start = (0,0)
self.goal = (self.size - 1,self.size - 1)
self.reset()
def reset(self):
self.state = self.start #回到起点
return self.state
def step(self,state,action):
x,y = state
if action == "up" : x = max(0,x - 1)
elif action == "down" : x = min(self.size - 1,x + 1)
elif action == "left" : y = max(0,y - 1)
elif action == "right" : y = min(self.size - 1,y + 1)
self.state = (x,y)
reward = 1.0 if self.state == self.goal else -0.1
done = self.state == self.goal #判断游戏是否结束
#time.sleep(1) # 每步暂停 0.3 秒
return self.state, reward,done
def get_actions(self):
return ["up","down","left","right"]
def render(self):
grid = [["⬜" for _ in range(self.size)] for _ in range(self.size)] #_仅表示一个占位符,grid是一个二维列表
x,y = self.state
gx,gy = self.goal
grid[gx][gy] = "🏁"
grid[x][y] = "🟩"
for row in grid:
print(" ".join(row)) #" ".join(row) 会把这几个元素用空格 " " 连接成一个字符串
print() #打印一个空行
# 用来模拟“某个状态执行动作后的新状态”
def value_iteration(env,gamma = 0.9,threshold = 0.01):
#如果一次迭代中,所有状态的价值变化都很小(小于 threshold),就认为已经“收敛”了,也就是说差不多已经是最优解了,就可以 停止迭代。
value_table = np.zeros((env.size,env.size)) #状态价值表
while (1):
delta = 0
for x in range(env.size):
for y in range(env.size):
state = (x,y)
if state == env.goal:
continue
action_values = [] #动作价值
for action in env.get_actions():
next_state,reward,done = env.step(state,action)
action_value = reward + gamma * value_table[next_state[0],next_state[1]] #贝尔曼公式
action_values.append(action_value)
max_action_value = max(action_values)
delta = max(delta, abs(value_table[x, y] - max_action_value)) #价值更新的差值
value_table[x, y] = max_action_value
if delta < threshold:
break
return value_table
#提取每个状态的最优动作(即策略)
def extract_policy(value_table,env,gamma = 0.9):
policy = np.full((env.size,env.size)," ",dtype=object) #存储最优策略
for x in range(env.size):
for y in range(env.size):
state = (x,y)
if state == env.goal:
continue
action_values = []
for action in env.get_actions():
next_state,reward,done = env.step(state,action)
action_value = reward + gamma * value_table[next_state[0], next_state[1]]
action_values.append(action_value)
best_action = env.get_actions()[np.argmax(action_values)] #action_values是价值列表,取价值最大的action的序号i,get_actions()[i]对应的动作就是最优动作
policy[x,y] = best_action
return policy
#打印最优策略
def render_policy(policy, env):
arrow_map = {
"up": "⬆",
"down": "⬇",
"left": "⬅",
"right": "➡",
" ": " " # 空白用于目标状态
}
print("最优策略图:")
for x in range(env.size):
row = ""
for y in range(env.size):
if (x, y) == env.goal:
row += "🏁 "
else:
row += arrow_map[policy[x, y]] + " "
print(row)
#最优策略应用到agent
def run_agent(env,policy):
state = env.reset()
env.render()
steps = 0
while state != env.goal:
action = policy[state]
state, reward, done = env.step(state,action)
env.render()
steps += 1
if done:
print("✔️successful pass!")
break
if __name__ == "__main__":
env = GridWorld()
values = value_iteration(env)
print("最终状态价值表:")
print(np.round(values, 2))
policy = extract_policy(values, env)
render_policy(policy, env)
print("智能体开始执行最优策略:")
run_agent(env, policy)
- 输出
最终状态价值表:
[[0.46 0.62 0.8 ]
[0.62 0.8 1. ]
[0.8 1. 0. ]]
最优策略图:
⬇ ⬇ ⬇
⬇ ⬇ ⬇
➡ ➡ 🏁
智能体开始执行最优策略:
🟩 ⬜ ⬜
⬜ ⬜ ⬜
⬜ ⬜ 🏁
⬜ ⬜ ⬜
🟩 ⬜ ⬜
⬜ ⬜ 🏁
⬜ ⬜ ⬜
⬜ ⬜ ⬜
🟩 ⬜ 🏁
⬜ ⬜ ⬜
⬜ ⬜ ⬜
⬜ 🟩 🏁
⬜ ⬜ ⬜
⬜ ⬜ ⬜
⬜ ⬜ 🟩
✔️successful pass!
进程已结束,退出代码为 0
3.Q-learning
- 上面的MDP中策略提取部分,就是在一个已知环境,根据贝尔曼方程,计算出最优的状态价值V(s),再推导出最优策略,这是动态规划的方法,前提是我们知道环境的所有信息(状态、动作、转移概率)
- Q-learning 的目标是学习一个“评分表”(称为 Q-table),告诉你在某个特定位置(状态 s)选择某个特定方向(动作 a) 最终能获得多少总分(累积奖励)。这个分数就是 Q 值,记为Q(s,a)
- 引入RL的核心思想:在未知环境下智能体通过交互学会最优策略,Q-learning是一种无模型基于值的强化学习算法
$$
Q(s_t,a_t)\leftarrow Q(s_t,a_t) + \alpha[r_{t+1} + \gamma \cdot \max_{a’}(Q(S_{t+1},a^‘) - Q(s_t,a_t)) ]
$$
-
上述为核心公式,其中Q(s,a) :在状态s下采取动作a取得的回报 | α:学习率 | $r_{t+1}$:在时刻t执行动作a后的即时奖励 | $\gamma$:衰减因子
-
公式含义:通过对当前Q值进行更新,使当前Q值向目标值靠近
- 目标值:贝尔曼方程计算得出,即当前动作带来的即时奖励$r_{t+1}$ + 下一状态得到的最大期望未来回报,即$\gamma \cdot \max_{a’}(Q(S_{t+1},a^‘)$
- 理解:当前的Q值可能是猜的,或者是初始化值(因为qlearning是在未知环境下),而目标值是看到了奖励+猜测下一状态的最大收益
-
学习的过程 - 学习是如何进行的
-
每次选择动作 - 探索 or 利用
- 探索:随机选择一个动作执行
- 利用:选择当前Q值最大的动作
-
如何更新Q值
- 目标值怎么来
- 在一次次尝试中得到即时奖励r和下一个状态s'
- 从已有的Q表中查s'的最大Q值(初始可能为0),这个值就作为目标值,用于更新当前的Q
- Q值更新
- 有了目标值,更新Q值的过程就是从当前值往目标值靠,即$Q_{s_t,a_t} \leftarrow Q_{s_t,a_t} + \alpha \cdot(目标值 - 当前估计)$
best_next_q = max([Q.get((next_state,a),0.0)for a in env.get_actions()]) current_q = Q.get((state,action),0.0) Q[state,action] = current_q + alpha * (reward + gamma * best_next_q - current_q) - 目标值怎么来
-
-
代码实现:初始化一个Q表,每个元素是一个键值对,key为(state,action),Value为Q值,设定一个训练轮数episodes开始训练,每轮训练都是从起点开始,重复执行:有10%的概率“探索”,即随机选择一个动作,然后执行,更新状态和q值,有90%的概率执行“利用”,即选择当前状态下可获得最大q值的动作,然后执行,更新状态和q值,直到到达终点,结束本轮训练。
#Q-learning
#episodes:训练总回合数,epsilon:探索率,智能体随机选择动作的概率,0.1即10%的时间随机探索,90%的时间利用已知信息
def q_learning(env,episodes = 500,alpha = 0.1, gamma = 0.9, epsilon = 0.1):
#Q-table 存储了在特定状态(state)下执行特定动作(action)的预期未来总回报(Q值)
Q = {} #Q表初始化,key:(state,action),value:Q值
for ep in range(episodes):
state = env.reset()
while (1):
if (np.random.rand() < epsilon):
action = np.random.choice(env.get_actions()) #探索(10%的时间) - 随机选择一个动作
else:
q_vals = [Q.get((state,a),0.0) for a in env.get_actions()]
action = env.get_actions()[np.argmax(q_vals)] #利用 - 选择Q值最大的动作
#执行动作
next_state,reward,done = env.step(state,action)
#更细Q值
best_next_q = max([Q.get((next_state,a),0.0)for a in env.get_actions()])#查找在next_state下哪个动作最佳 - 用于以后的“利用”
current_q = Q.get((state,action),0.0)
Q[state,action] = current_q + alpha * (reward + gamma * best_next_q - current_q) #qlearning公式
state = next_state
if done:
break #停止当前轮循环,开启下一轮,相当于一个训练的过程
return Q
- 也可以将q表打印出来
def print_q_table(Q, env):
data = []
for x in range(env.size):
for y in range(env.size):
state = (x, y)
row = {'state': state}
for action in env.get_actions():
row[action] = round(Q.get((state, action), 0.0), 2)
data.append(row)
df = pd.DataFrame(data)
print("\n📋 Q 表(每个状态对应的动作 Q 值):")
print(df.to_string(index=False))
Q = q_learning(env)
print_q_table(Q, env)
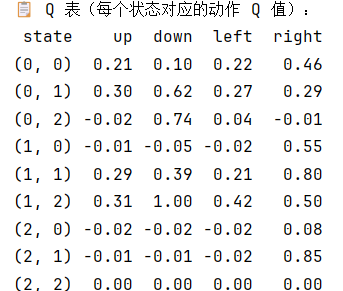
- 应用Q-learning
#从训练后的Q表中提取最优策略
def extract_policy_from_q(Q,env):
policy = {}
for x in range(env.size):
for y in range(env.size):
state = (x,y)
if state == env.goal:
continue
q_vals = [Q.get((state,a),0.0) for a in env.get_actions()]
best_action = env.get_actions()[np.argmax(q_vals)]
policy[state] = best_action
return policy #policy是一个二维矩阵
#agent使用qlearning
def run_agent_with_q(env,policy):
state = env.reset()
env.render()
steps = 0
while state != env.goal:
action = policy[state]
state,reward,done = env.step(state,action)
env.render()
steps += 1
if done:
print(f"到终点辣,用了 {steps}步")
break
if __name__ == "__main__":
env = GridWorld()
Q = q_learning(env) #得到训练后的Q表
policy = extract_policy_from_q(Q,env)
run_agent_with_q(env,policy)





 浙公网安备 33010602011771号
浙公网安备 33010602011771号