导数与微分的联系

导数与微分的联系

导数和微分的联系

1. 导数

   从物理的角度看，以牛顿为代表的数学家，在研究速度时，为了表示瞬时变化率，而引出了以下的等式：

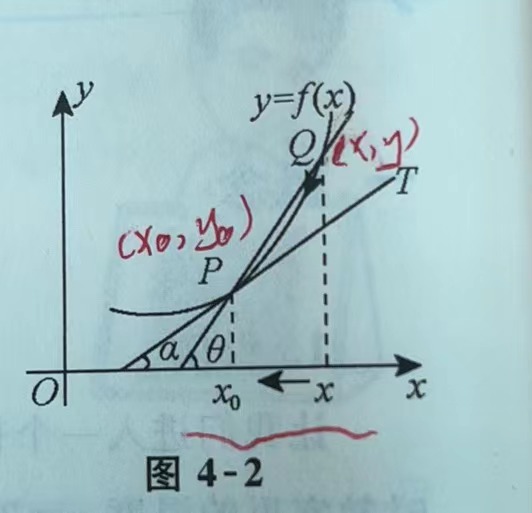
   \[lim_{\Delta t\rightarrow0}\frac{\Delta S}{\Delta t} = S'(t) = v(t) \]

   从几何的角度看，曾经很长一段时间，人们对于切线的定义是五花八门，千奇百怪，但又无法精确定义，直到莱布尼兹给出如下的解释：

   

   令Q沿着曲线向P靠近，直到无限趋近于P，此时直线PT则是曲线在P点处的切线。

   而对于切线的斜率，可以有以下表示：

   \[lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}=k \]

   数学就是要将具体情境抽象化，尽可能统一地描述事务，因此，将以上的例子抽象化，我们可以说：

   导数就是：\(\frac{函数增量}{自变量增量}\)对于某个自变量的极限。

   数学描述（增量式）：

   \[f'(x)=lim_{\Delta x\rightarrow0}\frac{\Delta y}{\Delta x}=lim_{\Delta x\rightarrow0}\frac{f(x_0-\Delta x)-f(x_0)}{\Delta x} \]

   数学描述（差值式）：

   \[f'(x_0)=lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0} \]

2. 微分

   • 引例

     \(y = f(x) = x^2\)

     \(\Delta y=(x+\Delta x)^2-x^2=2x\cdot\Delta x+(\Delta x)^2\)

     由于\((\Delta x)^2=o(\Delta x)\)，即高阶无穷小，因此\((\Delta x)^2\)对于\(\Delta x\)是忽略不计的，因此

     \(\Delta y=2x\cdot\Delta x\) ==> \(dy=2x\cdot\Delta x\)

     由于\(f'(x)=2x\)以及\(dx=\Delta x\)，因此

     \(dy=f'(x)dx\)

   • 引例解释

     • \(dy\)是怎么定义的？

       当函数增量可以写成：\(\Delta y=A\Delta x+o(\Delta x)\) 时，我们定义\(dy=A\Delta x\)

     • 为什么A就等于\(f'(x)\)呢？

       可以证明，这里不讨论。

     • 为什么\(dx=\Delta x\)呢？

       因为\(\Delta x=1\cdot\Delta x + 0\)，由上面可知\(dx=1\cdot\Delta x=\Delta x\)

     • 这个引例是可微的，那为什么它可微呢？

       一、\((\Delta x)^2\)对于\(\Delta x\)是忽略不计的

       二、\(2x=A\)

       可微的通俗理解：可微就是可以将函数增量写成一个简单的量加上一个可以忽略的高阶无穷小。

     • 可微和可导的联系？

       可微和可导互为充要条件，可以这么理解：在光滑的曲线上是可导的，因此存在切线，即可以用一段切线近似代替该点处的曲线，而产生的误差可以忽略不计，这就是可微。