Quantum Metrology

State after Beam Splitter

Refer to page 9 of ^[1]

\[|1\rangle |0\rangle \\ \left( \begin{matrix} \cos \frac{\phi}{2}& -\sin \frac{\phi}{2}\\ \sin \frac{\phi}{2}& \cos \frac{\phi}{2}\\ \end{matrix} \right) \left( \begin{array}{c} {a_{in}}^{\dagger}\\ {b_{in}}^{\dagger}\\ \end{array} \right) =\left( \begin{array}{c} {a_{out}}^{\dagger}\\ {b_{out}}^{\dagger}\\ \end{array} \right) \\ \left( \begin{array}{c} {a_{in}}^{\dagger}\\ {b_{in}}^{\dagger}\\ \end{array} \right) =\left( \begin{matrix} \cos \frac{\phi}{2}& \sin \frac{\phi}{2}\\ -\sin \frac{\phi}{2}& \cos \frac{\phi}{2}\\ \end{matrix} \right) \left( \begin{array}{c} {a_{out}}^{\dagger}\\ {b_{out}}^{\dagger}\\ \end{array} \right) =\left( \begin{array}{c} \cos \frac{\phi}{2}{a_{out}}^{\dagger}+\sin \frac{\phi}{2}{b_{out}}^{\dagger}\\ -\sin \frac{\phi}{2}{a_{out}}^{\dagger}+\cos \frac{\phi}{2}{b_{out}}^{\dagger}\\ \end{array} \right) \\ |1\rangle |0\rangle ={a_{in}}^{\dagger}|0\rangle |0\rangle =\left( \cos \frac{\phi}{2}{a_{out}}^{\dagger}+\sin \frac{\phi}{2}{b_{out}}^{\dagger} \right) |0\rangle |0\rangle \\ =\cos \frac{\phi}{2}|1\rangle |0\rangle +\sin \frac{\phi}{2}|0\rangle |1\rangle \]

Quantum Fisher Information^[2]

\[\frac{L_{\lambda}\rho _{\lambda}+\rho _{\lambda}L_{\lambda}}{2}=\partial _{\lambda}\rho _{\lambda} \\ \partial _{\lambda}p\left( x|\lambda \right) =Tr\left[ \partial _{\lambda}\rho _{\lambda}\Pi _x \right] \\ =Tr\left[ \frac{L_{\lambda}\rho _{\lambda}+\rho _{\lambda}L_{\lambda}}{2}\Pi _x \right] \\ =Tr\left[ \frac{L_{\lambda}\rho _{\lambda}}{2}\Pi _x \right] +Tr\left[ \frac{\rho _{\lambda}L_{\lambda}}{2}\Pi _x \right] \\ =\mathrm{Re}\left( Tr\left[ \rho _{\lambda}\Pi _xL_{\lambda} \right] \right) \\ F\left( \lambda \right) =\int{dx}\frac{\mathrm{Re}\left( Tr\left[ \rho _{\lambda}\Pi _xL_{\lambda} \right] \right) ^2}{Tr\left[ \rho _{\lambda}\Pi _x \right]}\le \int{dx}\left| \frac{Tr\left[ \rho _{\lambda}\Pi _xL_{\lambda} \right]}{\sqrt{Tr\left[ \rho _{\lambda}\Pi _x \right]}} \right|^2 \\ =\int{dx}\left| Tr\left[ \frac{\rho _{\lambda}\Pi _xL_{\lambda}}{\sqrt{Tr\left[ \rho _{\lambda}\Pi _x \right]}} \right] \right|^2=\int{dx}\left| Tr\left[ \frac{\sqrt{\rho _{\lambda}}\sqrt{\Pi _x}}{\sqrt{Tr\left[ \rho _{\lambda}\Pi _x \right]}}\sqrt{\Pi _x}L_{\lambda}\sqrt{\rho _{\lambda}} \right] \right|^2 \\ \le \int{dx}\left| Tr\left[ \frac{\sqrt{\rho _{\lambda}}\sqrt{\Pi _x}}{\sqrt{Tr\left[ \rho _{\lambda}\Pi _x \right]}}\frac{\sqrt{\Pi _x}\sqrt{\rho _{\lambda}}}{\sqrt{Tr\left[ \rho _{\lambda}\Pi _x \right]}} \right] ^{\frac{1}{2}}Tr\left[ \sqrt{\rho _{\lambda}}L_{\lambda}\sqrt{\Pi _x}\sqrt{\Pi _x}L_{\lambda}\sqrt{\rho _{\lambda}} \right] ^{\frac{1}{2}} \right|^2 \\ =\int{dx}Tr\left[ \sqrt{\rho _{\lambda}}L_{\lambda}\sqrt{\Pi _x}\sqrt{\Pi _x}L_{\lambda}\sqrt{\rho _{\lambda}} \right] \\ =Tr\left[ \rho _{\lambda}{L_{\lambda}}^2 \right] \\ if\,\,\frac{\sqrt{\Pi _x}\sqrt{\rho _{\lambda}}}{\sqrt{Tr\left[ \rho _{\lambda}\Pi _x \right]}}=a\sqrt{\Pi _x}L_{\lambda}\sqrt{\rho _{\lambda}}\,\,with\,\,real\,\,a. \\ Tr\left[ \rho _{\lambda}\Pi _xL_{\lambda} \right] =Tr\left[ \sqrt{\rho _{\lambda}}\sqrt{\Pi _x}\sqrt{\Pi _x}L_{\lambda}\sqrt{\rho _{\lambda}} \right] \\ =Tr\left[ \sqrt{\rho _{\lambda}}\sqrt{\Pi _x}\frac{\sqrt{\Pi _x}\sqrt{\rho _{\lambda}}}{\sqrt{Tr\left[ \rho _{\lambda}\Pi _x \right]}} \right] \frac{1}{a} \\ =real\,\,number\,\, \]

Error propagation formula^[3]

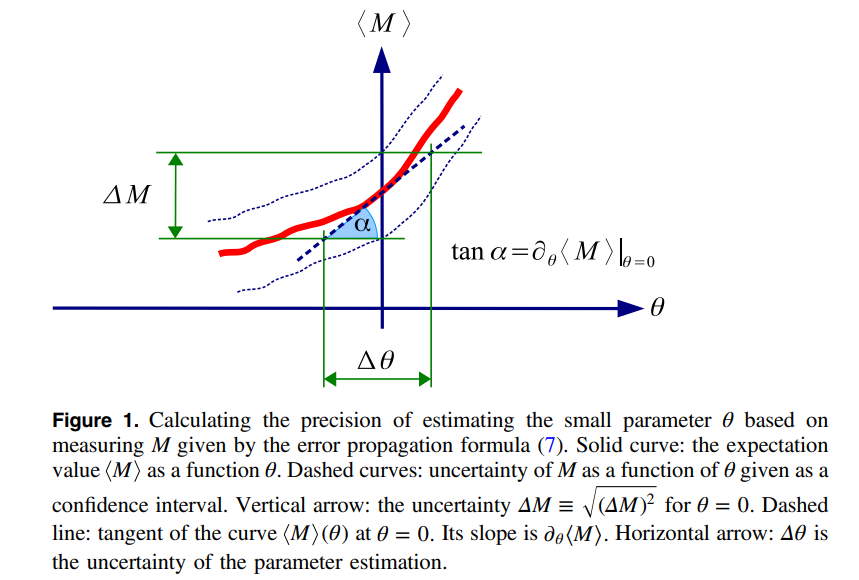
\[\left< \left( \theta -\left< \theta \right> \right) ^2 \right> \left| \partial _{\theta}\langle M\rangle |_{\theta =\theta _0} \right|^2=\left< \left( \left( \theta -\left< \theta \right> \right) \partial _{\theta}\langle M\rangle |_{\theta =\theta _0} \right) ^2 \right> \approx \left< \left( M-\left< M \right> \right) ^2 \right> \]

So we have: \((\Delta \theta )^2=\frac{(\Delta M)^2}{\left| \partial _{\theta}\langle M\rangle |_{\theta =\theta _0} \right|^2}\).

More rigorous proof may refer to this link.

---

1. E. Polino, M. Valeri, N. Spagnolo, and F. Sciarrino, Photonic Quantum Metrology, ArXiv:2003.05821 [Quant-Ph] (2020). ↩︎

2. QUANTUM ESTIMATION FOR QUANTUM TECHNOLOGY | International Journal of Quantum Information, https://www.worldscientific.com/doi/abs/10.1142/S0219749909004839. ↩︎

3. G. Tóth and I. Apellaniz, Quantum Metrology from a Quantum Information Science Perspective, J. Phys. A: Math. Theor. 47, 424006 (2014). ↩︎