【大二病也要学离散！】第十四章 格与布尔代数

今天的三部曲，第一章，格与布尔代数.

14.1 格的定义及性质

首先声明:本章的\(\wedge\)和\(\vee\)不是合取和析取，而表示最大下界和最小上界.
下面分别是格在偏序集和代数结构的两个定义.
设\(\langle S,\preccurlyeq \rangle\)是偏序集，若\(\forall x,y \in S,\{x,y\}\)均有最小上界和最大下界，则\(S\)关于\(\preccurlyeq\)构成一个格.
设\(\langle S,*,\circ \rangle\)是代数系统，\(*\)和\(\circ\)是二元运算，若\(*\)和\(\circ\)满足交换律、结合律和吸收律，则\(\langle S,*,\circ \rangle\)构成一个格.
注意:幂等律可以由吸收律推导出，因此不要求.
注意:最小上界和最大上界是唯一的.
定义:集合\(B\)的幂集\(P(B)\)关于\(\subseteq\)构成一个格，称\(\langle P(B),\subseteq \rangle\)为\(B\)的幂集格.
定义:\(G\)是群，\(L(G)\)是其所有子群的集合，即\(L(G)=\{H | H \leqslant G\}.\)其关于\(\subseteq\)构成一个格，易得\(H_1 \wedge H_2=H_1 \cap H_2,H_1 \vee H_2=\langle H_1 \cup H_2 \rangle.\)
数据仓库:使用物化视图，采用格的结构.
设\(p\)为含有格中元素以及符号\(=,\preccurlyeq,\succcurlyeq,\wedge,\vee\)的命题，令\(p^*\)是将\(p\)中的\(\preccurlyeq\)替换为\(\succcurlyeq,\)将\(\succcurlyeq\)替换为\(\preccurlyeq,\)将\(\wedge\)替换为\(\vee,\)将\(\vee\)替换为\(\wedge\)所得到的命题，则称\(p^*\)为\(p\)的对偶命题.
对偶原理:若\(p\)对一切格为真，则\(p^*\)也对一切格为真.
于是，我们能推出下列定理.
设\(\langle L,\preccurlyeq \rangle\)是格，则运算\(\vee\)和\(\wedge\)满足交换律、结合律、幂等律和吸收律.
(1) \(\forall a,b \in L,a \vee b=b \vee a,a \wedge b=b \wedge a.\)
(2) \(\forall a,b,c \in L,(a \vee b) \vee c=a \vee (b \vee c),(a \wedge b) \wedge c=a \wedge (b \wedge c).\)
(3) \(\forall a \in L,a \vee a=a,a \wedge a=a.\)
(4) \(\forall a,b \in L,a \vee (a \wedge b)=a,a \wedge (a \vee b)=a.\)
从而推出以下定理:
设\(\langle S,*,\circ \rangle\)是具有两个二元运算的代数系统，且\(*\)和\(\circ\)运算满足交换律、结合律和吸收律，则可以适当定义\(S\)上的偏序\(\preccurlyeq,\)使得\(\langle S,\preccurlyeq \rangle\)构成一个格，且\(\forall a,b \in S,a \wedge b=a*b,a \vee b=a \circ b.\)
我们还有关于格的一些运算性质,设\(L\)是格.
(1) \(\forall a,b \in L,a \preccurlyeq b \Leftrightarrow a \wedge b=a \Leftrightarrow a \vee b =b.\)
(2) \(\forall a,b,c,d \in L,\)若\(a \preccurlyeq b,c \preccurlyeq d,\)则\(a \wedge c \preccurlyeq b \wedge d,a \vee c \preccurlyeq b \vee d.\)
(3) \(\forall a,b,c \in L,a \vee (b \wedge c) \preccurlyeq (a \vee b) \wedge (a \vee c).\)
设\(\langle L,\wedge,\vee \rangle\)是格，\(S\)是\(L\)的非空子集，若\(S\)关于\(L\)中的运算\(\wedge\)和\(\vee\)仍构成格，则称\(S\)是\(L\)的子格.
注意:子格仍然满足原格中的性质，比如\(e \wedge f=c,c \notin S_1,\)则\(S_1\)不是子格.

14.2 分配格、有补格和布尔代数

设\(\langle L,\wedge,\vee \rangle\)是格，若\(\forall a,b,c \in L\)有\(a \wedge (b \vee c)=(a \wedge b) \vee (a \wedge c),a \vee (b \wedge c)=(a \vee b) \wedge (a \vee c).\)成立，则称\(L\)为分配格.

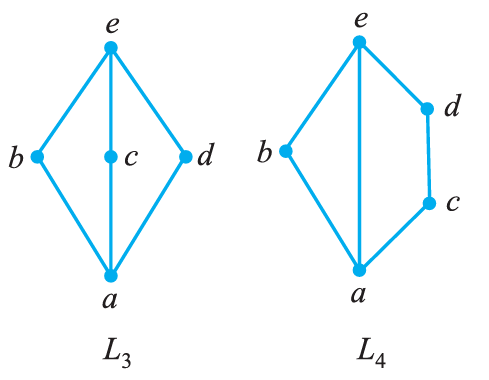
如图\(L_3\)所示的哈斯图称为钻石格，若图\(L_4\)所示的哈斯图称为五角格.
注意:钻石格的特点是三条单链，五角格的特点是一条单链和一条双链，因此中间那条连不连无所谓.
我们给出以下定理，设\(L\)是格:
(1) \(L\)是分配格当且仅当\(L\)中不含与钻石格和五角格同构的子格.
(2) 小于五元的格都是分配格.
(3) 任何一条链都是分配格.
(4) \(L\)是分配格当且仅当\(\forall a,b,c \in L,a \vee b=a \vee c,a \wedge b=a \wedge c,\)则\(b=c.\)
注意:若要用定义证明分配格，只需证明其中一个等式.
为引入有补格的概念，我们先介绍以下概念:
设\(L\)是格，若存在\(a \in L\)使得\(\forall x \in L,a \preccurlyeq x,\)则称\(a\)为\(L\)的全下界，若存在\(b \in L\)使得\(\forall x \in L,x \preccurlyeq b,\)则称\(b\)为\(L\)的全上界.
注意:若存在全下界或全上界，则一定是唯一的.我们通常将全下界记为\(0,\)全上界记为\(1.\)
设\(L\)为格，若\(L\)存在全下界和全上界，则称其为有界格，并将\(L\)记作\(\langle L,\wedge,\vee,0,1 \rangle.\)
注意:在有界格中，\(0\)是关于\(\wedge\)的零元，\(\vee\)的单位元；\(1\)是关于\(\wedge\)的单位元，\(\vee\)的零元.若对偶命题中存在\(0,\)则要把它换成\(1;\)反之则要换成\(0.\)
设\(\langle L,\wedge,\vee,0,1 \rangle\)为有界格，\(a \in L,\)若存在\(b \in L,a \wedge b=0,a \vee b=1,\)则称\(b\)为\(a\)的补元.
注意:补元是相互的。
注意:对于\(\wedge\)和\(\vee\)运算，若两个数可比,则一定在它们之间，反之则沿着哈斯图向上或者向下走.
注意:在任何有界格中，\(0\)和\(1\)都是互补的，其他的元素可能有补元，也可能没有补元；有补元可能唯一，可能不唯一.对于有界分配格，如果它的元素存在补元，则其唯一.
定理:设\(\langle L,\wedge,\vee,0,1 \rangle\)是有界分配格，若\(a \in L,\)且对于\(a\)存在补元\(b,\)则\(b\)是\(a\)的唯一补元.
设\(\langle L,\wedge,\vee,0,1 \rangle\)是有界格，若\(\forall a \in L,a\)在\(L\)中都存在补元，则称其为有补格.
若一个格是有补分配格，则称它为布尔格或布尔代数.
设\(\langle B,*,\circ \rangle\)是代数系统，\(*\)和\(\circ\)是二元运算.若\(*\)和\(\circ\)满足:
(1) 交换律，\(\forall a,b \in B,a*b=b*a.a \circ b=b \circ a.\)
(2) 分配律，\(\forall a,b,c \in B,a*(b \circ c)=(a*b)\circ (a*c).\)
(3) 同一律，存在\(0,1 \in B,\forall a \in B,a*1=a,a \circ 0=a.\)
(4) 补元律，\(\forall a \in B,\)存在\(a' \in B,a*a'=0,a \circ a'=1.\)
则称\(\langle B,*,\circ \rangle\)是布尔代数.
注意:有补格中每个元素都存在唯一的补元，可以把求补元的运算当做布尔代数中的一种一元运算，记作\(\langle B,\wedge,\vee,',0,1 \rangle.\forall a \in B,a'\)是\(a\)的补元.
布尔代数有以下性质:
设\(\langle B,\wedge,\vee,',0,1 \rangle\)是布尔代数，则
(1) \(\forall a \in B,(a')'=a.\)
(2) \(\forall a,b \in B,(a \wedge b)'=a' \vee b',(a \vee b)'=a' \wedge b'.\)
注意:(1)称为双重否定律,(2)称为德摩根律.
注意:德摩根律对于有限个元素都是正确的.
注意:\(B\)是任意集合，\(B\)的幂集格\(\langle P(B),\cap,\cup,\sim,\emptyset,B \rangle\)构成布尔代数，称作集合代数.

设\(L\)是格，\(0 \in L,0 \neq a \in L.\)若\(\forall b \in L,\)当\(0 \prec b \preccurlyeq a,b=a.\)称\(a\)为\(L\)中的原子.
于是有以下定理:
(1) 设\(B\)是有限布尔代数，\(A\)是\(B\)的全体原子组成的集合，则\(B\)同构于\(A\)的幂集代数\(P(A).\)
(2) 任何有限布尔代数的基数为\(2^n.\)
(3) 任何等势的有限布尔代数都是同构的.

下面是一些容易错的题目:
1.注意:判断是不是布尔代数，先判断是不是格.
注意:判断是不是格，先考虑是否其下界可比.
注意:证明子格也要先证非空，然后证明对\(\wedge\)和\(\vee\)封闭(或是运算律)
注意:如果是链只有\(0\)和\(1\)有补元.

2.求证:
(1) \((a \wedge b) \vee b=b.\)
(2) \((a \wedge b) \vee (c \wedge d) \preccurlyeq (a \vee c) \wedge (b \vee d).\)
思路:这种思路都是证明两边小于等于.
证明:(1) 易知\((a \wedge b) \vee b \succcurlyeq b,\)又由于\(b \succcurlyeq b,b \succcurlyeq (a \wedge b),\)得\((a \wedge b) \vee b \preccurlyeq b,\)因此\((a \wedge b) \vee b=b.\)
(2) 由于\(a \wedge b \preccurlyeq a \preccurlyeq a \vee c,a \wedge b \preccurlyeq b \preccurlyeq b \vee d,\)得\(a \wedge b \preccurlyeq (a \vee c) \wedge (b \vee d),\)同理有\(c \wedge d \preccurlyeq (a \vee c) \wedge (b \vee d).\)得\((a \wedge b) \vee (c \wedge d) \preccurlyeq (a \vee c) \wedge (b \vee d).\)

3.注意:给定\(\mathrm{lcm},\mathrm{gcd}\)是布尔代数.

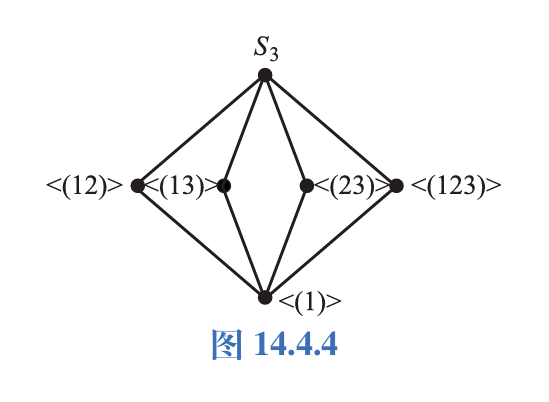
4.画出三元对称群\(S_3\)的子群格.
答案:如图所示

5.小结论:设\(L\)为格，若\(a_1 \wedge a_2 \wedge a_3 \ldots a_n=a_1 \vee a_2 \vee a_3 \ldots a_n,\)则\(a_1=a_2 \ldots a_n.\)

6.设\(\langle L,\preccurlyeq \rangle\)是格，任取\(a \in L,\)令\(S=\{x \in L | x \preccurlyeq a\}.\)求证:\(\langle S,\preccurlyeq \rangle\)是\(S\)的子格.
思路:按照前面说的证明子格的思路来.
证明:由于\(a \in S,\)因此\(S\)非空.
\(\forall x,y \in S,x \preccurlyeq a,y \preccurlyeq a,\)因此\(x \vee y \preccurlyeq a \preccurlyeq a=a,x \wedge y \preccurlyeq a,\)从而有关于这两种运算封闭，即为子群.

7.给定下列集合和运算，判断是哪一类代数系统.
(1) \(S_1=\{1,\frac{1}{2},2,\frac{1}{3},3,\frac{1}{4},4\},*\)为普通乘法.
答案:不是代数系统，因为不封闭.

8.\(S_4=\{1,2,3,6\},\forall x,y \in S,x \circ y\)和\(x*y\)分别表示求最大公因数和最小公倍数.
答案:是格，也是布尔代数.这两个运算满足交换律和结合律，求最小公倍数运算的单位元是\(1,\)求最大公因数的单位元是\(6,\)满足同一律和补元律.

9.设\(B\)是布尔代数，则\(\forall a,b \in B,a \preccurlyeq b \Leftrightarrow a \wedge b'=0 \Leftrightarrow a' \vee b=1.\)

9.对于\(n=1,2,3,4,5,\)给出所有不同构的\(n\)元格.
答案: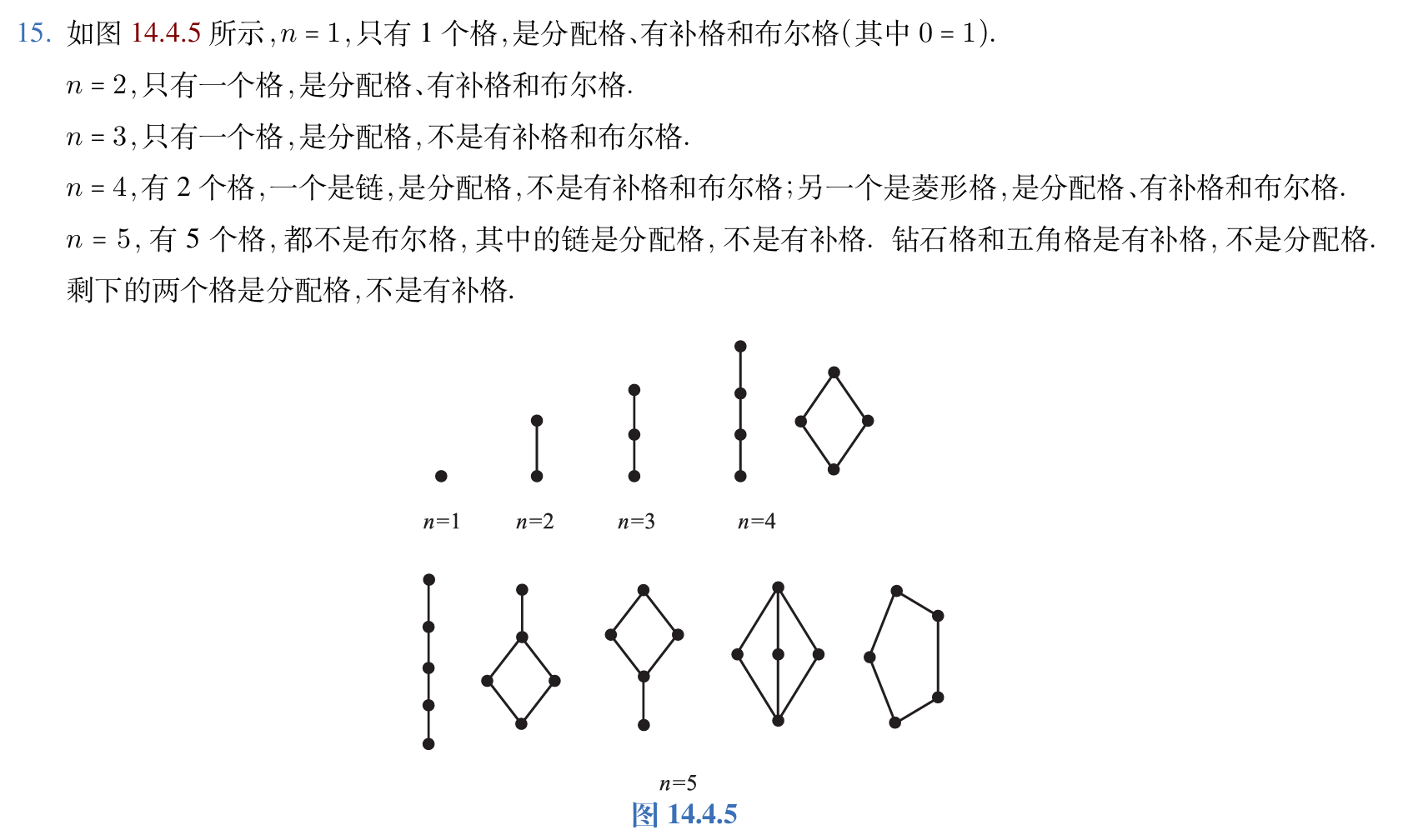

10.设\(B=\langle \wedge,\vee,',0,1 \rangle\)是布尔代数，在\(B\)上定义二元运算\(\oplus:\forall x,y \in B,x \oplus y=(x \wedge y') \vee (x' \wedge y).\)
问:\(\langle B,\oplus \rangle\)能否构成代数系统？如果能，指出是哪一种代数系统.
证明:是群，易知原运算是封闭的.
下面证明结合律:

\[\begin{align*} (x \oplus y) \oplus z & =((x \wedge y') \vee (x' \wedge y)) \oplus z \\ & = (((x \wedge y') \vee (x' \wedge y)) \wedge z') \vee (((x \wedge y') \vee (x' \wedge y))' \wedge z) \\ & = (x \wedge y' \wedge z') \vee (x' \wedge y \wedge z') \vee (x' \wedge y' \wedge z) \vee (x \wedge y \wedge z) \\ \end{align*}\]

\[\begin{align*} x \oplus (y \oplus z) & =x \oplus ((y \wedge z') \vee (y' \wedge z)) \\ & =(x' \wedge ((y \wedge z') \vee (y' \wedge z))) \vee (x \wedge ((y \wedge z') \vee (y' \wedge z))') \\ & = (x \wedge y' \wedge z') \vee (x' \wedge y \wedge z') \vee (x' \wedge y' \wedge z) \vee (x \wedge y \wedge z) \\ \end{align*}\]

同时有，\(0\)是单位元，\(x\)的逆元就是其自身，因此是群.

11.小结论:设\(B\)是布尔代数，\(\forall a,b,c \in B,\)若\(a \preccurlyeq c,\)则有\(a \vee (b \wedge c)=(a \vee b) \wedge c.\)

12.设\(B\)是布尔代数，\(a_1,a_2,\ldots a_n \in B,\),则有\((a_1 \vee a_2 \vee \ldots \vee a_n)'=a_1' \wedge a_2' \ldots \wedge a_n',(a_1 \wedge a_2 \ldots \wedge a_n)'=a_1' \vee a_2' \ldots \vee a_n'.\)

13.设\(B_1,B_2,B_3\)是布尔代数，证明:若\(B_1 \cong B_2,B_2 \cong B_3,\)则\(B_1 \cong B_3.\)
证明:由于\(f:B_1 \rightarrow B_2,g:B_2 \rightarrow B_3,\)因此\(f \circ g:B_1 \rightarrow B_3\)也是双射.下面证明其为同态映射.\(\forall x,y \in B_1,f \circ g(x \wedge y)=g(f(x) \wedge f(y))=g(f(x)) \wedge g(f(y))=f \circ g(x) \wedge f \circ g(y).\)
\(f \circ g(x')=g(f(x)')=g(f(x))'=f \circ g(x)'.\)
因此其为同态映射，且\(B_1 \cong B_3.\)

14.设\(L=\langle Z_12,\oplus \rangle\)的子群格，给出\(L\)的所有\(4\)元子格.
答案:共有\(\{\langle 0 \rangle,\langle 4 \rangle,\langle 6 \rangle,\langle 2 \rangle\},\{\langle 6 \rangle,\langle 3 \rangle,\langle 2 \rangle,\langle 1 \rangle\},\{\langle 0 \rangle,\langle 4 \rangle,\langle 3 \rangle,\langle 1 \rangle\},\{\langle 0 \rangle,\langle 4 \rangle,\langle 2 \rangle,\langle 1 \rangle\},\{\langle 0 \rangle,\langle 6 \rangle,\langle 2 \rangle,\langle 1 \rangle\},\{\langle 0 \rangle,\langle 6 \rangle,\langle 3 \rangle,\langle 1 \rangle\}.\)

15.设\(G=\langle Z_5,\oplus \rangle\).令\(G\)上所有自同构构成的群为\(\mathrm{Aut} \ G,\)给出其运算表并画出它的子群格\(L\)的哈斯图.
答案: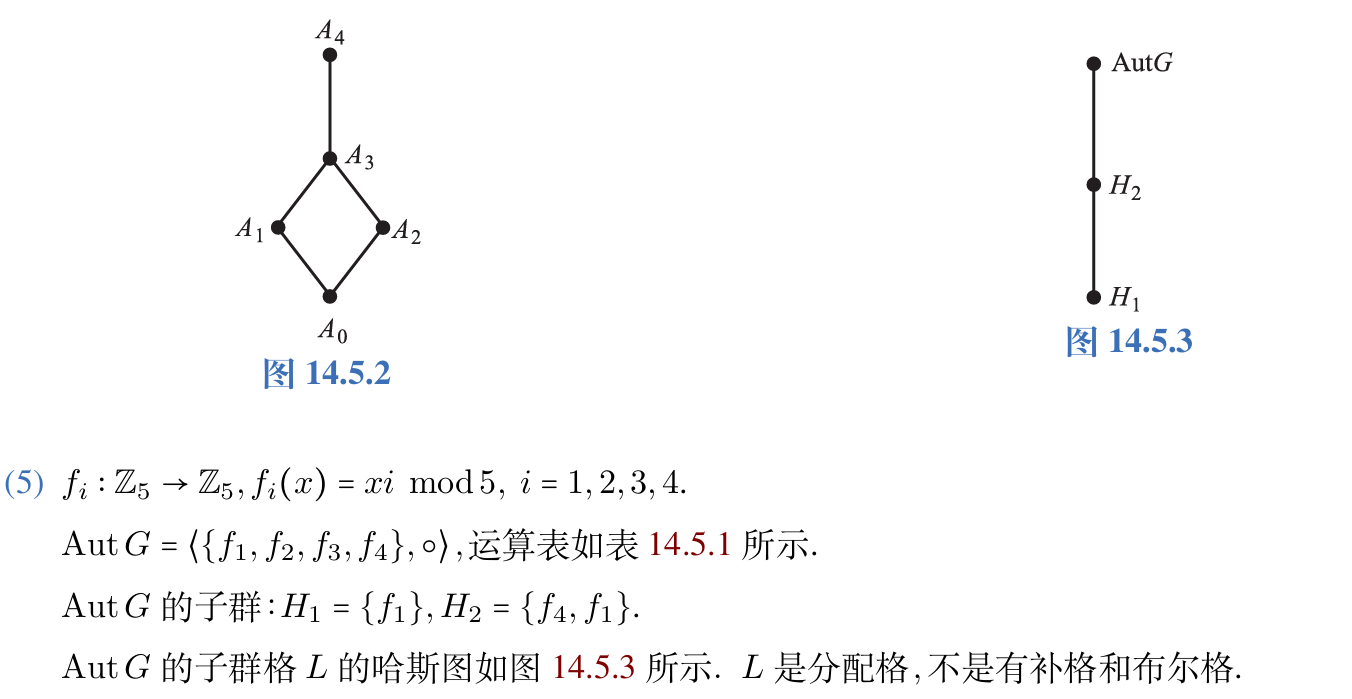

16.设\(I\)是格\(L\)的非空子集，如果满足下列条件，称\(I\)为理想:
(i) \(\forall a,b \in I,a \vee b=I.\)
(ii) \(\forall a \in I,\forall x \in L,x \preccurlyeq a \rightarrow x \in I\).
证明:\(I\)是\(L\)的子格.
证明:由题意，\(I\)非空且\(\vee\)封闭，又由于\(\forall a,b \in I,a \wedge b \preccurlyeq a,\)因此\(a \wedge b \in I.\)

17.在格\(L\)中,\(\forall a,b,c \in L,a \wedge (b \vee c)=(a \wedge b) \vee (a \wedge c),\)求证\(\forall a,b,c \in L,a \vee (b \wedge c)=(a \vee b) \wedge (a \vee c).\)
思路:考虑拓展.
证明:\((a \vee b) \wedge (a \vee c)=((a \vee b) \wedge a) \vee ((a \vee c)\wedge c)=a \vee ((a \wedge c) \vee (b \wedge c))=(a \vee (a \wedge c)) \vee (b \wedge c)=a \vee (b \wedge c).\)

下学期，也请各位继续关注：
《System beats!》
《大二病也要学离散！》
《数算の旅》
《某信息学的概率统计》
还有——

《我的算法竞赛不可能这么可爱》

本期到此结束！