【大二病也要学离散！】第十二章 代数系统

今明两天我们要把代数结构的三章学完
剩下的逻辑就不难了

12.2 二元运算及其性质

设\(S\)为集合，函数\(f:S \times S \rightarrow S\)称为\(S\)上的二元运算，简称为二元运算.
封闭、不封闭的概念
一个运算是否为\(S\)上的二元运算:
(1) \(S\)中任意两个元素都可以进行这种运算，且运算结果唯一.
(2) \(S\)中任意两个元素的运算结果都属于\(S,\)即\(S\)对该运算是封闭的.
通常用\(\circ,*,\cdot\)等符号表示二元运算，称为算符.
设\(S\)为集合，函数\(f:S \rightarrow S\)称为\(S\)上的一个一元运算，简称为一元运算，用算符记作\(\circ(x)=y\)或\(\circ x=y.\)
二元运算的主要性质:
(1) 交换律，例如相对补，矩阵乘法\(A^A\)上函数的复合不是可交换的
(2) 结合律,例如函数的复合运算是可结合的
(3) 若\(\forall x \in S,x \circ x=x,\)则称其满足幂等律.若某些\(x\)满足\(x \circ x=x,\)称它们为幂等元.若\(S\)上的二元运算满足幂等律，则\(S\)中的所有元素都是幂等元.例如加法和乘法、相对补和对称差运算不满足幂等律.
(4) 给定\(S\)上的两个二元运算\(\circ\)和\(*,\)若\(\forall x,y,z \in S,x*(y \circ z)=(x * y)\circ (x * z),(y \circ z)*x=(y*x) \circ (z*x).\)则称\(*\)对\(\circ\)是可分配的，或称\(*\)对\(\circ\)满足分配律.
注意:通常应该指明哪个运算对哪个运算可分配，因为往往只有一个运算对另一个运算满足分配律，反之不对.
注意:用归纳法可证若\(*\)对\(\circ\)分配律成立，则广义分配律也成立.
注意:对单个运算不能考虑分配律.
(5) 若\(\circ\)和\(*\)是\(S\)上两个可交换的二元运算，如果\(\forall x,y \in S,x*(x \circ y)=x,x \circ (x*y)=x,\)则称\(\circ\)和\(*\)满足吸收律.
(6) 左单位元、右单位元和单位元(幺元),若同时存在左右单位元，则它们相等且为唯一的单位元.
(7) 左零元、右零元和零元，若同时存在左零元和右零元，则它们相等且为唯一的零元.
(8) 若\(\circ\)是\(S\)上的二元运算，\(e\)和\(\theta\)分别为\(\circ\)的单位元和零元，若\(S\)至少有两个元素，则\(e \neq \theta.\)
(9) 左逆元、右逆元、逆元(可逆)
(10) 设\(\circ\)是\(S\)上可结合的二元运算，\(e\)为该运算的单位元，若\(x \in S\)存在左逆元和右逆元，则它们相等且为\(x\)唯一的逆元.
注意:单位元和零元都是相对与运算本身而言的，而逆元是相对于元素而言.不同的元素对应着不同的逆元，有的元素没有逆元.
(11) 设\(\circ\)为\(S\)上的二元运算，若\(\forall x,y,z \in S,\)有\(x \circ y = x \circ z,x \neq \theta, \rightarrow y=z,y \circ x = z \circ x,x \neq \theta, \rightarrow y=z\)前者称为左消去律，后者称为右消去律，两者合称消去律，注意被消去的数不能是零元.

12.2 代数系统

非空集合\(S\)和\(S\)上\(k\)个一元或二元运算\(f_1,f_2,\ldots,f_k\)组成的系统称作一个代数系统，简称为代数，记作\(\langle S,f_1,f_2,\ldots,f_k \rangle.\)
代数系统中的特定元素，称这些元素为该代数系统的特异元素或代数常数，也可以把这些代数常数列到系统的表达式中，在不发生混淆的情况下，为了叙述的简便也常用集合的名字来标记代数系统.
若两个代数系统中运算的个数相同，对应运算的元数想通，且代数常数的个数也相同,那么称这两个代数系统具有相同的构成成分，也称它们是同类型的代数系统.
注意:同类型的代数系统只是具有相同的构成成分，不一定有相同的运算性质.
若同类型的两个代数系统具有共同的运算性质，那么称它们是同种的.
若规定了代数系统的构成成分，即集合、运算以及代数常数，若再限制运算的算律，那么满足这些条件的代数系统就有完全相同的性质
比如，\(\langle S,\circ \rangle,\)其中\(\circ\)是可结合的二元运算，那么它是一类代数系统，即半群.
比如，\(\langle S,\circ,* \rangle,\)其中\(\circ\)和\(*\)是二元运算，并满足交换律、结合律、幂等律和吸收律，那么它是一种一类代数系统，即格.
由已知的代数系统通过系统的方法构成新的代数系统:
设\(V=\langle S,f_1,f_2,\ldots,f_k \rangle\)是代数系统，\(B \subseteq S,\)如果\(B\)对运算\(f_1,f_2,\ldots,f_k\)都是封闭的，且\(B\)和\(S\)含有相同的代数常数，那么称\(\langle B,f_1,f_2,\ldots,f_k \rangle\)是\(V\)的子代数系统，简称为子代数，有时简记为\(B.\)
注意:对于任何代数系统，其子代数一定存在，最大的子代数就是\(V\)本身.如果\(V\)中所有代数常数构成的集合对\(V\)中所有的运算都是封闭的，那么它构成了\(V\)的最小子代数.这种最大和最小子代数称为\(V\)的平凡子代数.若\(B\)是\(S\)的真子集，则\(B\)构成的子代数称为\(V\)的真子代数.
注意:在真子代数中不存在空集的概念，因此最小子代数既是平凡子代数，又是真子代数.
设\(V_1=\langle A,\circ \rangle\)和\(V_2=\langle B,* \rangle\)是同类型的代数系统，\(\circ\)和\(*\)是二元运算，在集合\(A \times B\)上定义二元运算\(\cdot\),\(\forall \langle a_1,b_1 \rangle,\langle a_2,b_2 \rangle \in A \times B,\langle a_1,b_1 \rangle \cdot \langle a_2,b_2 \rangle=\langle a_1 \circ a_2,b_1*b_2 \rangle.\)则称\(V=\langle A \times B,\cdot \rangle\)为\(V_1\)和\(V_2\)的积代数,记作\(V_1 \times V_2.\)此时也称\(V_1\)和\(V_2\)为\(V\)的因子代数.
关于积代数的一些定理:
设\(V_1=\langle A,\circ \rangle\)和\(V_2=\langle B,* \rangle\)是同类型的代数系统，\(V_1 \times V_2=\langle A \times B,\cdot \rangle\)是它们的积代数.
(1) 如果\(\circ\)和\(*\)满足交换律、结合律、幂等律，那么\(\cdot\)也满足交换律、结合律和幂等律.
(2) 如果\(e_1(\theta_1)\)和\(e_2(\theta_2)\)分别为\(\circ\)和\(*\)的单位元(零元)，那么\(\langle e_1,e_2 \rangle(\langle \theta_1,\theta_2 \rangle)\)也是\(\cdot\)的单位元(零元).
(3) 如果\(x\)和\(y\)分别为\(\circ\)和\(*\)的可逆元素，那么\(\langle x,y \rangle\)也是\(\cdot\)运算的可逆元素，其逆元就是\(\langle x^{-1},y^{-1} \rangle.\)
注意:积代数的定义可以推广到具有多个运算的同类型的代数系统，积代数也保留因子代数中的分配律、吸收律等性质，但是不一定保留消去律.

12.3 同态与同构

设\(V_1=\langle A,\circ \rangle\)和\(V_2=\langle B,* \rangle\)是同类型的代数系统，\(f:A \rightarrow B,\)且\(\forall x,y \in A\)有\(f(x \circ y)=f(x)*f(y).\)则称\(f\)是从\(V_1\)到\(V_2\)的同态映射,简称为同态.
注意:同构有自反性、对称性与传递性.
若\(f\)为单射，称为单同态；若为满射则称为满同态，此时称\(V_2\)是\(V_1\)的同态像;若\(f\)为双射，称其为同构，也称代数系统\(V_1\)同构于\(V_2,\)记作\(V_1 \cong V_2.\)
若同态映射\(f\)是从\(V\)到\(V\)的，那么称\(f\)为自同态，同样有单自同态、满自同态、同构的概念.
若\(V_1=\langle A,\circ \rangle\)和\(V_2=\langle B,* \rangle,f\)是从\(V_1\)到\(V_2\)的同态映射，那么若\(\circ\)具有交换律、结合律、幂等律等(消去律)可能是例外，则\(*\)也具有相同算律.同时，\(f\)把\(V_1\)的单位元\(e_1\)映射到\(V_2\)的单位元\(e_2,\)即\(f(e_1)=e_2.\)同样对于零元和可逆元也有\(f(\theta_1)=\theta_2,f(x^{-1})=f(x)^{-1}.\)
上述关于同态映射的定义可以推广到具有有限多个运算的代数系统.例如，\(V_1=\langle A,\circ_1,\circ_2, \rangle\)和\(V_2=\langle B,*_1,*_2 \rangle,f:A \rightarrow B,\)如果\(\forall x,y \in A,\)有\(f(x \circ_1 y)=f(x)*_1f(y),f(x \circ_2 y)=f(x)*_2f(y),\)那么\(f\)是从\(V_1\)到\(V_2\)的同态映射.
零同态:全映射到零.
证明恰有\(n\)个\(V\)的自同态的思路:证明其有\(n\)个自同态，然后证明任意自同态都是其中一员.
进程代数:见书.

下面是一些容易错的题目:
1.通过运算表判断运算律和代数常数的办法:
交换律是容易发现的
幂等律也是容易发现的
如果在运算表的某行或者某列(除了零元所在的行列)有两个值相等，那么不满足消去律.
单位元和零元是容易发现的
幂等元也是容易发现的
对于结合律，只需判断除单位元和零元之外的元素，认真发现可能破坏结合律的元素并加以验证.

2.注意:求单位元时要满足左右单位元均满足.
注意:不可交换也可能存在单位元或者零元.
注意:逆元不一定在原集合中.
注意:任何减法都没有零元.

3.注意:能构成代数系统，关键在于满足运算的定义.

4.注意:写同态像的时候，应用子代数的形式表示，同时并不是只有满自同态才有同态像.

5.下列集合和运算是否构成代数系统？如果构成，说明该系统是否满足交换律、结合律，求出该运算的单位元、零元和所有可逆元素的逆元.
(6) \(A=Z,x*y=x+y+xy,\)这里\(+\)为普通加法.
答案:构成；交换、结合，单位元0,零元-1，可逆元为0和-2.

6.对于下列集合和二元运算，判断\(A\)上是否封闭.如果是封闭的，那么指出它是否满足交换律、结合律，是否有零元和单位元.
(1) \(A=P(\{a,b\}),X*Y=X \cup Y.\)
(3) \(A\)是非空集合\(B\)上所有二元关系的关系矩阵集合，\(*\)为关系矩阵乘法(相加采用逻辑加).
(4) \(A=nZ=\{nk | k \in Z\},n\)是正整数，\(*\)为普通乘法.
(6) \(A\)是非空集合\(B\)上所有等价关系的集合,\(R_1 * R_2=R_1 \cup R_2.\)
答案:(1) 封闭，交换，结合，单位元是\(\emptyset,\)零元是\(\{a,b\}.\)
(3) 封闭，可结合，仅当\(B\)为单元集时可交换；单位元是单位矩阵，零元是全0矩阵.
(4) 封闭，可交换，可结合，单位元是空集，没有零元.
(6) 当\(|B|<3\)时，\(B\)上的全部等价关系只有恒等关系和全域关系，运算封闭；此时运算满足交换律和结合律，单位元是恒等关系，零元是全域关系.当\(|B| \ge 3\)时，两个等价关系的并集不一定具有传递性，运算不封闭.

7.设\(V=\langle A,\oplus \rangle,\)其中\(A=P(\{1,2,3\}),\oplus\)为集合的对称差，试给出\(V\)的所有子代数，并说明哪些是平凡子代数，哪些是真子代数.
答案:平凡子代数:\(B_1=\{\emptyset \},V.\)
非平凡子代数:
2元的:\(B_2=\{\emptyset,\{1\}\},B_3=\{\emptyset,\{2\}\},B_4=\{\emptyset,\{3\}\},B_5=\{\emptyset,\{1,2\}\},B_6=\{\emptyset,\{1,3\}\},B_7=\{\emptyset,\{2,3\}\},B_8=\{\emptyset,\{1,2,3\}\}.\)
4元的:\(B_9=\{\emptyset,\{1\},\{2\},\{1,2\}\},B_{10}=\{\emptyset,\{1\},\{3\},\{1,3\}\},B_{11}=\{\emptyset,\{2\},\{3\},\{2,3\}\}\)
\(B_{12}=\{\emptyset,\{1\},\{2,3\},\{1,2,3\}\},B_{13}=\{\emptyset,\{2\},\{1,3\},\{1,2,3\}\},B_{14}=\{\emptyset,\{3\},\{1,2\},\{1,2,3\}\}.\)

8.设\(A=\{0,1\},S=A^A.\)，请写出\(S\)上合成运算的运算表.

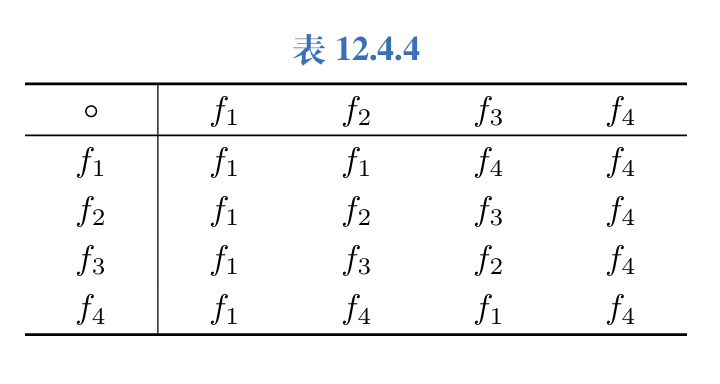
9.设\(A=\{a,b,c\},\)能否确定\(a,b,c\)的值使得
(1) \(A\)对普通乘法封闭.
(2) \(A\)对普通加法封闭.
答案:(1) 可以,\(A=\{-1,0,1\}\)
(2) 不可以.

10.给定\(n \in Z^+,nZ=\{nz | z \in Z\},nZ\)关于普通的加法和乘法运算.请找出它的单位元、零元和所有可逆元素的逆元.
答案:加法单位元\(0,\)没有零元,每个元素\(x\)都可逆，其逆元为它的相反数\(-x\).当\(n=1\)时，乘法有单位元\(1,\)只有两个可逆元素，\(1\)和\(-1\).当\(n>1\)时没有单位元和可逆元素，乘法有零元\(0\).

11.设\(S\)为\(n\)元集，\(S\)上可以定义多少个不同的二元运算和一元运算？其中有多少个二元运算是可交换的？有多少个二元运算是幂等的？有多少个二元运算既不是可交换的，又不是幂等的？
答案:\(n^{n^2}\)个不同的二元运算，\(n^n\)个不同的一员运算，可交换的运算有\(n^{\frac{n^2+n}{2}}\)个，幂等的运算有\(n^{n^2-n}\)个，交换并且幂等的运算有\(n^{\frac{n^2-n}{2}}\)个，既不交换又不幂等的运算有\(n^{n^2}-(n^{\frac{n^2+n}{2}}+n^{n^2-n})+n^{\frac{n^2-n}{2}}.\)

12.下列集合都是\(N\)的子集，它们能否构成代数系统\(V=\langle N,+ \rangle\)的子代数?
(1) \(\{x|x \in N,x\)的某次幂可以被\(16\)整除\(\}.\)
答案:题目中所述即为偶数，因此能构成.

13.设代数系统\(V=\langle 2Z,+ \rangle,\)其中\(2Z=\{2k | k \in Z\},+\)为普通加法，求\(V\)的子代数.
答案:子代数为\(2nZ.\)

下学期，也请各位继续关注：
《System beats!》
《大二病也要学离散！》
《数算の旅》
《某信息学的概率统计》
还有——

《我的算法竞赛不可能这么可爱》

本期到此结束！