【大二病也要学离散！】第九章 支配集、覆盖集、独立集、匹配与着色

今天我们来学习图论的最后一部分.
这部分定义还是比较多的，所以我们慢慢看.
注意:前三节我们都是在无向简单图中讨论，而最后一节我们在无环无向图中讨论.

9.1 支配集、点独立集与点覆盖集

设无向简单图\(G=\langle V,E \rangle,V^* \subseteq V,\)若\(\forall v_i \in V-V^*,\exists v_j \in V^*\)使得\((v_i,v_j) \in E,\)则称\(V^*\)为\(G\)的一个支配集，并称\(v_j\)支配\(v_i.\)设\(V^*\)是\(G\)的支配集，且\(V^*\)的任何真子集都不是支配集，则称\(V^*\)为极小支配集.\(G\)的顶点最少的支配集称为最小支配集，最小支配集中顶点的个数称作\(G\)的支配数，记作\(\gamma_0(G),\)简记为\(\gamma_0.\)
设无向简单图\(G=\langle V,E \rangle,V^* \subseteq V,\)若\(V^*\)中任何两个顶点都不相邻，则称\(V^*\)为\(G\)的点独立集,简称为独立集.若\(V^*\)中再加入任何其他的顶点都不是独立集，则称\(V^*\)为极大点独立集;\(G\)中顶点数最多的点独立集称作\(G\)的最大点独立集,最大点独立集的顶点数称作\(G\)的点独立数，记为\(\beta_0(G),\)简记为\(\beta_0.\)
设无向简单图\(G=\langle V,E \rangle,V^* \subseteq V,\)若\(\forall e \in E, \exists v \in V^*,\)使得\(v\)与\(e\)相关联，则称\(V^*\)为\(G\)的点覆盖集，简称为点覆盖，并称\(v\)覆盖\(e.\)设\(V^*\)是\(G\)的点覆盖，若\(V^*\)的任何真子集都不是点覆盖，则称\(V^*\)为极小点覆盖.\(G\)的顶点个数最少的点覆盖称为\(G\)的最小点覆盖，最小点覆盖中的顶点个数称作\(G\)的点覆盖数，记作\(\alpha_0(G)\),简记为\(\alpha_0.\)
上面三个定义的区别:支配是与其他顶点都相邻，点独立是自己不相邻，覆盖是&点覆盖边.
相关定理:
(1) 设无向简单图\(G=\langle V,E \rangle\)没有孤立点，则\(G\)的极大点独立集都是极小支配集.
注意:这个命题的逆命题是不成立的，极小支配集不一定是极大点独立集.
(2) 设无向简单图\(G=\langle V,E \rangle\)没有独立点，\(V^* \subseteq V,\)则\(V^*\)为\(G\)的点覆盖当前仅当\(\overline{V^*}=V-V^*\)是\(G\)的点独立集.
(3) 设无向简单图\(G=\langle V,E \rangle\)是无孤立点的\(n\)阶无向图，\(V^* \subseteq V,\)则\(V^*\)是\(G\)的极小(最小)点覆盖当且仅当\(\overline{V^*}=V-V^*\)是\(G\)的极大(最大)点独立集，从而有\(\alpha_0+\beta_0=n.\)

9.2 边覆盖集与匹配

设无向简单图\(G=\langle V,E \rangle,E^* \subseteq E,\)若\(\forall v \in V,\exists e \in E^*,\)使得\(v\)与\(e\)相关联，则称\(E^*\)为边覆盖集，简称为边覆盖，并称\(e\)覆盖\(v.\)设\(E^*\)为\(G\)的边覆盖，若\(E^*\)的任何真子集都不是边覆盖，则称\(E^*\)为极小边覆盖.\(G\)的边数最少的边覆盖称为\(G\)的最小边覆盖，最小边覆盖中的边数称作\(G\)的边覆盖数，记作\(\alpha_1(G),\)简记为\(\alpha_1.\)
注意:当图有孤立点时不存在边覆盖.
设无向简单图\(G=\langle V,E \rangle,E^* \subseteq E,\)若\(E^*\)中任何两条边均不相邻，则称\(E^*\)为\(G\)的边独立集，也称作\(G\)的匹配.若在\(E^*\)中再加任意一条边后，所得集合都不是匹配，则称\(E^*\)是极大匹配.\(G\)的边数最多的匹配称作最大匹配，最大匹配中的边数称作边独立数或匹配数，记作\(\beta_1(G),\)简记为\(\beta_1.\)
注意:匹配和边覆盖的定义可以参照点独立和点覆盖记忆.
设\(M\)为\(G=\langle V,E \rangle\)的一个匹配:
(1) 称\(M\)中的边为匹配边，不在其中的边为非匹配边.
(2) 称与匹配边相关联的顶点为饱和点，不与匹配边相关联的顶点为非饱和点.
(3) 若\(G\)中每个顶点都是饱和点，则称\(M\)为\(G\)的完美匹配.
(4) \(G\)中由匹配边和非匹配边的交替构成的路径称作交错路径，起点和终点不同，且都是非饱和点的交错路径称作可增广的交错路径,\(G\)中由匹配边和非匹配边交替构成的圈称作交错圈.
注意:最大匹配不一定是完美匹配.
注意:可增广的交错路径中可增广的含义为:将匹配边变成非匹配边，非匹配边变成匹配边，得到的交错路径中匹配边数量比原来大1.
注意:完美匹配的必要条件是阶数为偶数.
注意:求最大匹配的步骤，首先找出一个极大匹配，然后找到一条可增广的交错路径，接着反转并验证.
下面给出一些定理:
设图\(G\)无孤立点:
(1) 设\(M\)为\(G\)的一个最大匹配，对\(G\)中每一个非饱和点取一条与之关联的边，组成边集\(N\),则\(W=M \cup N\)为\(G\)的最小边覆盖.
(2) 设\(W_1\)为\(G\)的一个最小边覆盖，若\(W_1\)中存在相邻的边就删去其中的一条，设移去的边集为\(N_1,\)则\(M_1=W_1-N_1\)为\(G\)的最大匹配.
(3) \(G\)的边覆盖数\(\alpha_1\)与匹配数\(\beta_1,\)满足\(\alpha_1+\beta_1=n.\)
(4) 设\(M\)是\(G\)的一个匹配，\(W\)是\(G\)的一个边覆盖，则\(|M| \le |W|,\)且当等号成立时，\(M\)是\(G\)的完美匹配，\(W\)是\(G\)的最小边覆盖.
注意:不饱和点的数量永远为\(n-2\beta_1,\)同时总有\(\beta_1 \le \alpha_1.\)
定理:设\(M\)为图\(G\)的一个匹配，则\(M\)为\(G\)的最大匹配当且仅当\(G\)中不含关于\(M\)的可增广的交错路径.

9.3 二部图中的匹配

设\(G=\langle V_1,V_2,E \rangle\)为二部图,\(|V_1| \le |V_2|,\)若\(M\)为\(G\)的一个匹配且\(|M|=|V_1|,\)则称\(M\)为从\(V_1\)到\(V_2\)的完备匹配.
注意:二部图的完备匹配是最大匹配，但最大匹配不一定是完备匹配.当\(|V_1|=|V_2|\)时，完备匹配是完美匹配.
给出二部图有完备匹配的充要条件，也称作相异性条件:
霍尔(\(\mathrm{Hall}\))定理:设二部图\(G=\langle V_1,V_2,E \rangle,\)其中\(|V_1| \le |V_2|,\)则\(G\)中存在从\(V_1\)到\(V_2\)的完备匹配当且仅当\(V_1\)中任何\(k,1 \ge k \ge |V_1|,\)个顶点至少与\(V_2\)中的\(k\)个顶点相邻.
给出二部图有完美匹配的充分条件,也称作\(t\)条件:
设二部图\(G=\langle V_1,V_2,E \rangle,\)如果存在正整数\(t\),使得\(V_1\)中每个顶点至少关联\(t\)条边，而\(V_2\)中每个顶点至多关联\(t\)条边，那么\(G\)中存在从\(V_1\)到\(V_2\)的完备匹配.
注意:求二分图最大匹配以及带权二分图的最大权匹配，详见算法书与Leetcode.

9.4 着色

注意:本节主要研究无环的无向图.
设无向图\(G\)无环，对\(G\)的每个顶点涂一种颜色，使相邻的顶点涂不同的颜色，称作图\(G\)的一种点着色，简称为着色.若能用\(k\)种颜色给\(G\)的顶点着色，则称\(G\)为\(k-\)可着色的，若\(G\)是\(k-\)可着色的，但不是\((k-1)-\)可着色的，则称\(G\)的色数为\(k\),图\(G\)的色数记作\(\chi(G),\)简记为\(\chi.\)
一些关于\(\chi\)的性质和定理:
(1) \(\chi(G)=1\)当且仅当\(G\)是零图.
(2) \(\chi(K_n)=n.\)
(3) 偶圈的色数为2,奇圈为3,奇阶轮图的色数为\(3,\)偶阶轮图的色数为\(4.\)
(4) 设\(G\)至少含一条边，则\(\chi(G)=2\)当且仅当\(G\)为二部图.
(5) 对于任意无环图\(G,\)均有\(\chi(G) \le \Delta(G)+1.\)
注意:这个上界当且仅当\(G\)是\(K_n,n \le 3\)或奇圈时达到.
(6) 布鲁克斯定理:设\(n \ge 3,\)若连通图\(G\)不是完全图\(K_n\),也不含奇圈，则\(\chi(G) \le \Delta(G).\)
求图的色数的方法:先判断它们是不是特殊图,再考虑布鲁克斯定理，最后考虑推导.
我们接下来给出下面的定义:
连接无桥平面图的平面嵌入及其所有的面称作地图,地图的面称作国家，若两个国家的边界至少有一条公共边，则称这两个国家相邻.
对地图\(G\)上的每个国家涂上一种颜色，使相邻的国家涂不同的颜色，称作对地图\(G\)的面着色.若能够用\(k\)种颜色给\(G\)的面着色，则称\(G\)为\(k-\)可面着色的.若\(G\)为\(k-\)可面着色的，但不是\((k-1)-\)可面着色的，则称\(G\)的面色数为\(k\).\(G\)的面色数记作\(\chi^*(G),\)简记为\(\chi^*.\)
对图\(G\)的每条边着一种颜色，使相邻的边着不同的颜色，称作对\(G\)的边着色.若能用\(k\)种颜色给\(G\)的边着色，则称\(G\)为\(k-\)可边着色的.若\(G\)为\(k-\)可边着色的，但不是\((k-1)-\)可边着色的，则称\(G\)的边色数为\(k\).\(G\)的边色数记作\(\chi'(G),\)简记为\(\chi'.\)
注意:上面讨论的图都是无环无向图.
注意:地图是无桥的平面图，因此它的对偶图无圈.
下面给出一些定理:
(1) 地图\(G\)是\(k-\)可面着色的当且仅当它的对偶图\(G^*\)是\(k-\)可着色的.
(2) 任何平面图都是4-可着色的.
(3) 维津(\(\mathrm{Vizing}\))定理:设\(G\)为简单图,则\(\Delta(G) \le \chi'(G) \le \Delta(G)+1.\)
(4) 二部图的边色数等于\(\Delta.\)
还有几个结论:
(1) 长度大于或等于\(2\)的偶圈的边色数等于\(2,\)长度大于或等于\(3\)的奇圈的边色数等于\(3.\)
(2) \(n \ge 4,\chi'(W_n)=n-1.\)
(3) 当\(n(n \not = 1)\)为奇数时，\(\chi'(K_n)=n,\)而当\(n\)为偶数时，\(\chi'(K_n)=n-1.\)

下面是一些容易错的题目:
1.
(1) 命题"若\(V^*\)为无向图\(G\)的最大点独立集，则\(V^*\)也是\(G\)的最小支配集"为真吗？为什么？ 答案:不一定，逆命题才是必然.
(2) 图的极小支配集不一定是点独立集.
(3) 图的极小支配集不一定是最小支配集.
(4) 图的极大点独立集不一定是最大点独立集.
(5) 图的极大匹配不一定是最大匹配.

2.求二部图中边不重的完备匹配.
(1) \(K_{2,3}\)中有多少个边不重的完备匹配? 答案:\(3\)个.
(2) \(K_{3,3}\)中有多少个边不重的完美匹配? 答案:\(3\)个.

3.设二部图\(G=\langle V_1,V_2,E \rangle,|V_1| \le |V_2|,M\)为\(G\)的一个匹配，\(\Gamma\)为一条\(M\)可增广的交错路径，\(M\)能是\(G\)中\(V_1\)到\(V_2\)的完备匹配吗？为什么？
解：由于存在可增广的交错路径，因此它不为最大匹配，更不可能是完备匹配.

4.求如图所示的无向图的点色数\(\chi\)和边色数\(\chi'.\)

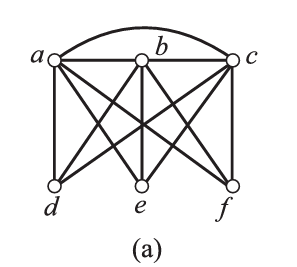
本题给我们一个启示:如果看到有圈或者完全图，要先考虑圈或者完全图.

5.设\(G\)是\(3-\)正则的哈密顿图，证明:\(G\)的边色数\(\chi'=3.\)
思路:这种题我们通常采用正反证明的方法来证，结合一下度数等知识.
证明:由于\(G\)为\(3-\)正则图，即\(\Delta(G)=3,\)因此\(\chi' \ge 3.\)下面证明:\(\chi' \le 3.\)
由于\(G\)为\(3-\)正则图，由握手定理知\(2m=3n,\)于是\(n\)为偶数.设\(C\)是\(G\)中的一条哈密顿回路，则\(C\)为\(n\)阶偶圈，因此可用两种颜色给其上色.\(G\)不在\(C\)上的边彼此不相邻，可用另外一种颜色给它们着色，因此\(\chi'=3.\)

6.证明:对于\(n \ge 3,\)在完全图\(K_n\)中，\(\beta_1<\alpha_0,\beta_0<\alpha_1.\)
思路:这种题通常对于特殊的图可以直接求出来相关数的.
证明:\(n \ge 3,\beta_1=\lfloor \frac{n}{2} \rfloor,\alpha_1=\lfloor \frac{n+1}{2} \rfloor,\beta_0=1,\alpha_0=n-1.\)于是可证.

7.证明:在完全二部图\(K_{r,s}\)中,\(\beta_1=\alpha_0,\beta_0=\alpha_1.\)
证明:\(\beta_1=\alpha_0=\mathrm{min}(r,s),\beta_0=\alpha_1=\mathrm{max}(r,s)\)

8.证明:对于任意的无向简单图\(G,\)均有\(\alpha_0 \ge \delta.\)
证明:设\(V_1\)为\(G\)的一个最小点覆盖集，则\(V_2=G-V_1\)为一个最大点独立集.由于\(V_2\)中顶点互不相邻，因此\(\forall v \in V_2,\)与\(v\)相邻的顶点均在\(V_1\)中，所以\(V_1\)中至少有\(\delta\)个顶点.

9.证明:在\(8 \times 8\)的国际象棋棋盘的一条主对角线上移去两端的方格后，所得棋盘不能用\(1 \times 2\)的长方形不重叠地填满.
思路:转化为二部图的完美匹配.

10.设二部图\(G=\langle V_1,V_2,E \rangle\)为\(k-\)正则图，证明:\(G\)中存在完美匹配，其中\(k \ge 1.\)
思路:我们必须考虑其中的性质.
证明:由于二部图为\(k-\)正则图，因此\(|V_1|=|V_2|.\)又由于它满足\(k\)条件，因此存在完备匹配，而完备匹配就是完美匹配.

11.设\(T\)是非平凡的无向树，证明:\(\chi(T)=2.\)
思路:书上的性质是\(\chi(G)=2\)当且仅当\(G\)为非平凡的二部图，而非平凡无向树就是二部图.

12.设\(G\)为\(n\)阶\(k-\)正则图，证明:\(\chi(G) \ge \frac{n}{n-k}.\)
证明:设\(v\)为\(G\)中任意一个顶点，\(d(v)=k.\)因此至多可以有\(n-k\)个顶点和\(v\)涂相同的颜色，于是至少需要\(\lfloor \frac{n}{n-k} \rfloor.\)种颜色.

13.证明:任何无环平面图都是\(6-\)可着色的.
证明:当\(n \le 6\)时是显然的，设当\(n=k>6\)时成立，则\(n=k+1\)时，由于平面图的性质知\(\delta \le 5.\)找到度数最小的顶点\(v,\)由归纳假设得\(G-v\)可\(6-\)着色，又由于\(v\)至多与\(5\)个顶点相邻，因此仍然可涂色.

14.证明:彼得松图的边色数\(\chi'=4.\)
证明太长，写不下了.

15.求彼得松图的\(\gamma_0,\beta_0,\beta_1,\alpha_0,\alpha_1.\)
答案:3,4,5,6,5.

16.含完全图\(K_n\)作为子图的无向图\(G\)的点色数至少为\(n.\)

17.设\(G\)是不含\(K_3\)的连通的简单平面图，求证:
(1) \(\delta(G) \le 3.\)
(2) \(G\)是\(4-\)可着色的.
思路:有了之前的经验之后，我们可以发现证出第一题之后，第二题就自然出来了.
证明:\((1)\) 当\(n \le 4,\)由已知条件知为真.
当\(n \ge 5,\)由连通性可知\(m \ge 3,\)又因为\(G\)中不含\(K_3,\)因此每个面至少由\(4\)条边围成，于是有\(4r \ge 2m,r \ge \frac{m}{2}.\)
若\(\delta(G) \ge 4,\)则由握手定理可得\(4n \le 2m,\)即\(n \le \frac{m}{2}.\)再由欧拉公式可知其矛盾.

下学期，也请各位继续关注：
《System beats!》
《大二病也要学离散！》
《数算の旅》
《某信息学的概率统计》
还有——

《我的算法竞赛不可能这么可爱》

本期到此结束！