【大二病也要学离散！】第八章 平面图

今天我们来学平面图，明天学完第九章图论部分就结束了.

8.1 平面图的基本概念

若能将无向图\(G\)画在平面上使得除顶点外无边相交，则称\(G\)为可平面图，简称平面图，画出的无边相交的图称作\(G\)的平面嵌入.无平面嵌入的图称作非平面图.
注意:一个平面图可以画出多个平面嵌入，但是它们都彼此同构.
常见的平面图:\(K_1,K_2,K_3,K_4,K_5-e,k_{1,n},k_{2,n},\)常见的非平面图:\(K_{3,3},K_5\).
定理:平面图的子图都是平面图，非平面图的母图都是非平面图.
定理:设\(G\)是平面图，则在\(G\)中加平行边或环后得到的图还是平面图.
给定平面图\(G\)的平面嵌入,它的边将平面划分为若干个区域，每个区域都称作\(G\)的一个面，其中有一个面的面积无限，称作无限面或者外部面，其余面的面积有限，称作有限面或者内部面.包围每个面的所有边组成的回路称作该面的边界，边界的长度称作该面的次数.
注意:组成回路的回路可能是圈、简单回路，也可能是复杂回路.
平面图的握手定理:平面图所有面的次数之和等于边数的两倍.
注意:在两个面的公共边界上的边算次数时，算1次；只在某一个面的边界上出现的边(即桥)算次数时，算2次.
设\(G\)为简单平面图，若\(G\)为\(K_i,(1 \ge i \ge 4),\)或者在\(G\)的任意两个不相邻的顶点之间加一条边，所得图均为非平面图，则称其为极大平面图.若在非平面图\(G\)中任意删除一条边，所得的图为平面图，则称\(G\)为极小非平面图.
注意:\(K_5-e\)为极大平面图,\(K_5\)和\(K_{3,3}\)都是极小非平面图.
定理:极大平面图是连通的，并且当阶数大于等于3时没有割点和桥.
定理:设\(G\)是\(n\)阶简单连通的平面图，则\(G\)为极大平面图当且仅当其每个面次数均为\(3\).

8.2 欧拉公式

设连通平面图\(G\)的顶点数，边数和面数分别为\(n,m,r\),设\(G\)每个面的次数至少为\(l(l \ge 3),\)则有以下定理:
(1) 欧拉公式:\(n-m+r=2\)
(2) \(m \ge \frac{l}{l-2}(n-2)\)
推论为下面定理:
对于有\(k\)个连通分支的平面图\(G\)，设\(G\)每个面的次数至少为\(l(l\ ge 3),\)则有以下定理:
(1) 欧拉公式:\(n-m+r=k+1\)
(2) \(m \ge \frac{l}{l-2}(n-k-1).\)

于是，可以推出\(K_5\)和\(K_{3,3}\)都是非平面图.
下面，我们考虑极大平面图与欧拉公式的关系:
定理:设\(G\)是\(n(n \ge 3)\)阶\(m\)条边的极大平面图，则\(m=3n-6.\)
推论:设\(G\)是\(n(n \ge 3)\)阶\(m\)条边的简单平面图，则\(m \le 3n-6.\)
定理:设\(G\)是简单平面图，则\(G\)的最小度\(\delta \le 5.\)

8.3 平面图的判断

设\(e=(u,v)\)为图\(G\)的一条边，在\(G\)中删除\(e\)，增加新的顶点\(w\)，使\(u,v\)均与\(w\)相邻，称作在\(G\)中插入2度顶点\(u\)，设\(w\)为\(G\)中的一个2度顶点，\(w\)与\(u,v\)相邻，删除\(w\)，添加新边\((u,v),\)称作在\(G\)中消去2度顶点\(w\).若两个图同构，或通过反复插入、消去2度顶点后同构,则称它们同胚.
库拉托夫斯基(\(\mathrm{Kuratowski}\))定理:
(1) 图\(G\)是平面图当且仅当\(G\)中既不含与\(K_5\)同胚的子图，也不含与\(K_{3,3}\)同胚的子图.
(2) 图\(G\)是平面图当且仅当\(G\)中既没有可以收缩到 \(K_5\) 的子图，也没有可以收缩到\(K_{3,3}\) 的子图.
注意:本节在判断非平面图的时候，还常用到"平面图的子图都是平面图，非平面图的母图都是非平面图"这个结论.
注意:完全图的任意一条边都是同构的.
注意:库拉托夫斯基定理只对\(K_5\)和\(K_{3,3}\)有效.

8.4 平面图的对偶图

设\(G\)是一个平面图的平面嵌入，构造图\(G^*\)如下:在\(G\)的每一个面\(R_i\)中放置一个顶点\(v_i^*.\)设\(e\)为\(G\)的一条边，若\(e\)在\(G\)的面\(R_i\)和\(R_j\)的公共边界上，则作边\(e^*=(v_i^*,v_j^*)\)与\(e\)相交，且不与其他任何边相交.若\(e\)为\(G\)中的桥且在面\(R_i\)的边界上，则作以\(v_i^*\)为端点的环\((v_i^*,v_i^*).\)称\(G^*\)为\(G\)的对偶图.
我们会发现，对偶图\(G^*\)有以下性质:
(1) \(G^*\)是平面图，而且是平面嵌入.
(2) \(G^*\)是连通图.
(3) 若\(e\)为\(G\)中的环，则\(G^*\)与\(e\)对应的边为桥;若\(e\)为桥，则\(G^*\)中与\(e\)对应的边为环.
(4) 在多数情况下，\(G^*\)为多重图(含平行边的图).
(5) 同一个平面图的不同平面嵌入的对偶图不一定同构.
同时，还有以下定理:
设平面图\(G\)是连通的，\(G^*\)是\(G\)的对偶图，\(n^*,m^*,r^*\)和\(n,m,r\)分别为\(G^*\)和\(G\)的顶点数、边数和面数，则有以下定理:
(1) \(n^*=r\)
(2) \(m^*=m\)
(3) \(r^*=n\)
(4) 设\(G^*\)的顶点\(v_i^*\)位于\(G\)的面\(R_i\)中，则\(d_{G^*}(v_i^*)=\mathrm{deg}(R_i).\)
推广到非连通图，则有以下定理:
设平面图\(G\)有\(k\)个连通分支，\(G^*\)是\(G\)的对偶图，\(n^*,m^*,r^*\)和\(n,m,r\)分别为\(G^*\)和\(G\)的顶点数、边数和面数，则有以下定理:
(1) \(n^*=r\)
(2) \(m^*=m\)
(3) \(r^*=n-k+1\)
(4) 设\(G^*\)的顶点\(v_i^*\)位于\(G\)的面\(R_i\)中，则\(d_{G^*}(v_i^*)=\mathrm{deg}(R_i).\)
注意:对偶图是连通图.
注意:画对偶图时，每条边都要穿过对应的边，包括环.
注意:对偶图满足的是\(n^*-m^*+r^*=2.\)

若\(G\)存在一个平面嵌入，使得\(G\)同构于对偶图\(G^*,\)那么称\(G\)为自对偶图.
设\(n \ge 4,\)在正\(n-1\)边形中放置一个顶点，连接它与这个正多边形上的所有顶点，得到的\(n\)阶简单图称为 \(n\)阶轮图.\(n\)为奇数的轮图称为奇阶轮图，反之称为偶阶轮图.轮图都是自对偶图.

1.题型:重新画某个图的平面嵌入，使得其外部面的边数为?
思路:任何一个面都可以作为外部面，所以考虑扩大某个面来包裹其他面.

2.
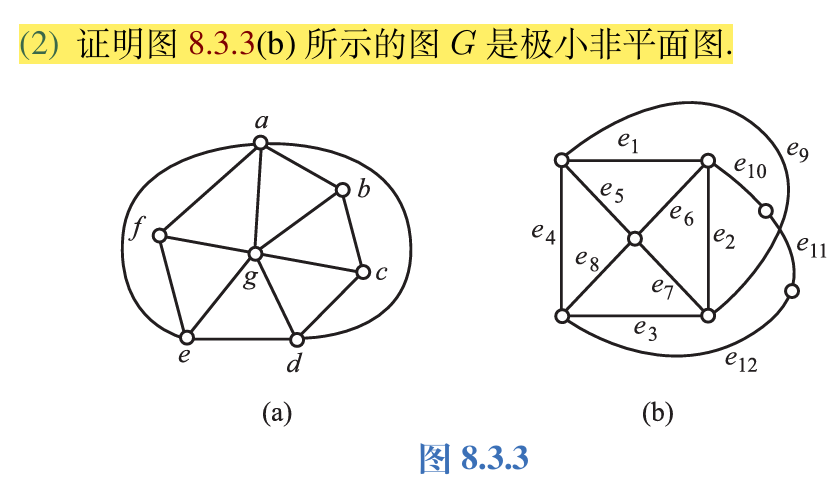
思路:这种题有两种思路，一种是从定义出发，证明删除每一条边后都为平面图，且原图为非平面图.第二种是利用两个库拉托夫斯基定理.

3.证明:不存在具有\(5\)个面且每两个面的边界都恰好共享一条公共边的平面图.
思路:证明这个一般从欧拉公式及其推论或者对偶图来实现.
证明:若存在这样的平面图，则其每个面的次数为\(4,\)从而它的对偶图的每个点度数为\(4,\)一共有\(5\)个顶点，成为了\(K_5.\)而\(K_5\)不是平面图，矛盾.

4.证明:极大平面图是连通的，并且当阶数大于或等于\(3\)时没有平面图.
思路:本题的证明思路作为参考.
证明:假设该极大平面图是非连通的，那么在两个连通分支间加上一条边，得到的仍是平面图，与极大平面图的定义矛盾.
假设\(G\)中存在割点\(v_0\)，割点的度数必然大于等于\(2\),不妨设\(v_1,v_2\)与\(v_0\)关联，删去\(v_0\)后，\(v_1,v_2\)位于两个连通分支中，画出每个分支的平面嵌入，并使它们相互分离，得到\(G - v_0\)的一个平面嵌入，再将\(v_0\)与它关联的边放入这个平面嵌入中，得到\(G\)的一个平面嵌入.可以添加\((v_1,v_2),\)使其不与\(G\)的边相交，即\(G \cup (v_1,v_2)\)仍为平面图，则与极大平面图的定义矛盾.
假设\(G\)中存在桥\(e=(u,v),\)由于\(G\)为极大非平面图，又\(n \ge 3,\)因此\(u,v\)中必有一个度数大于等于\(2,\)设\(d(u) \ge 2,\)则\(u\)为割点，前面已经证明没有割点，因此矛盾.
注意:割点的度数必然大于等于\(2\),如果\(n \ge 3,\)桥的两个端点中必然有一个度数$ \ge 2,$并且它是割点.

5.注意:由于平行边和环不改变平面性，因此如果给的图是非平面图，然后加一条平行边，问是否是极小非平面图，那么一定不是.

6.注意:本章中的题目大多数与点数、度数、面数等有关系.

7.设\(G\)是简单平面图，面数\(r<12,\delta(G) \ge 3.\)证明:\(G\)中存在次数小于或等于\(4\)的面.
证明:假设\(G\)中不存在次数小于或等于\(4\)的面，由欧拉定理得到\(n-m+r=2,\)又由于\(\delta(G) \ge 3,\)得到\(2m \ge 3n=3(m-r+2).\)由于\(G\)中每个面的次数大于等于\(5,\)得到\(2m \ge 5r.\)于是解这两个方程得到\(r \ge 12,\)矛盾.

8.画出全部非同构的\(6\)阶连通简单的非平面图.
思路:考虑\(K_{3,3}\)加边和\(K_5\)加一个顶点，于是就和书上的题目一样了.注意可能两道题得到的图有一部分是同构的.

9.小结论:设\(n\)阶\(m\)条边的平面图是自对偶图，则\(m=2m-2.\)

10.设\(G\)是\(n\)阶极大平面图，\(n \ge 4,\)证明\(G\)的对偶图\(G^*\)是\(2\)边\(-\)连通的\(3-\)正则图.
思路:这道题有的地方可能你会漏,比如证明没有桥，又比如正则图一定是简单图.
证明:由于\(G\)是极大平面图，因此它每个面的次数都等于\(3.\)因此，\(G^*\)每个顶点的度数都为\(3\).由于\(G\)无环无桥(比较容易忘记的定理)，因此 \(G^*\) 没有桥，又由于\(n \ge 4,\)因此\(G\)两个面的边界最多有一条边，因此\(G^*\)不含平行边，为简单图，因此它是\(2\)边\(-\)连通的\(3-\)正则图.

11.证明:平面图\(G\)的对偶图是欧拉图当且仅当\(G\)中每个面的次数都是偶数.
思路:这题还是跟欧拉公式等等有关系.
证明:充分性:由于\(G\)中每个面的次数都是偶数，因此\(G^*\)中不存在奇度顶点，又由于\(G^*\)必然连通，因此\(G^*\)为欧拉图.
必要性:由于\(G^*\)是欧拉图，因此它每个顶点的度数都为偶数，因此\(G\)中每个面的次数都是偶数.
综上，证毕.

12.小结论:设\(G^*\)为\(G\)的对偶图，\(G^{**}\)是\(G^*\)的对偶图，当\(G\)不连通的时候，\(G^{**}\)与\(G\)一定不同构.

13.命题"设\(G\)是任意\(n\)阶\(m\)条边的极大平面图，则\(m=3n-6\)"的真值为?
答案:为假，书上的结论要求\(n \ge 3.\)

下学期，也请各位继续关注：
《System beats!》
《大二病也要学离散！》
《数算の旅》
《某信息学的概率统计》
还有——

《我的算法竞赛不可能这么可爱》

本期到此结束！