【大二病也要学离散！】第六章 欧拉图与哈密顿图

今天来学一下第六章，欧拉图和哈密顿图
明天开树，都是之前学过比较熟的.

6.1 欧拉图和哈密顿图

通过图中每条边一次且仅一次并且过每一顶点的通路称作欧拉通路,通过图中每条边一次且仅一次并且过每一顶点的回路称作欧拉回路，具有欧拉通路的图称为半欧拉图，具有欧拉回路的图称为欧拉图.
注意:平凡图是欧拉图.
定理:无向图是欧拉图 \(\Leftrightarrow\) 它是连通图且无奇度顶点.
定理:无向图是半欧拉图 \(\Leftrightarrow\) 它是连通图且恰有两个奇度顶点.
定理:有向图是欧拉图 \(\Leftrightarrow\) 它是强连通的且每个顶点的入度等于出度.
定理:有向图是半欧拉图 \(\Leftrightarrow\) 它是单向连通的且恰有两个奇度顶点，其中一个顶点入度比出度大一，另一个顶点出度比入度大一.
定理:\(G\)是非平凡的欧拉图 \(\Leftrightarrow\) \(G\)是连通的且是若干个边不重的圈的并.
小结论:非平凡欧拉图\(G\)的\(\lambda(G) \ge 2.\)
求欧拉回路的算法:弗勒里算法
其内容为:任取\(G\)中一个点，延展与结尾点\(v_i\)相关联的边\(e_{i+1}\)，要求除非无别的边可选.否则\(e_{i+1}\)不能为\(G-\{e_1,e_2,\ldots,e_i\}\)中的桥.

6.2 哈密顿图

经过图中每个顶点一次且仅一次的通路称作哈密顿通路，经过图中每个顶点一次且仅一次的回路称作哈密顿回路，具有哈密顿通路的图称作半哈密顿图，具有哈密顿回路的图称作哈密顿图.
注意:平凡图是哈密顿图.
注意:哈密顿图尚未研究出充要条件，因此下列给出的都是充分条件或者必要条件.
定理:给定无向图\(G=\langle V,E \rangle\)为哈密顿图，则对于\(\forall V_1 \subset V,V_1 \not = V\)均有\(p(G-V_1) \le |V_1|.\)
推论:给定无向图\(G=\langle V,E \rangle\)为半哈密顿图，则对于\(\forall V_1 \subset V,V_1 \not = V\)均有\(p(G-V_1) \le |V_1|+1.\)
二部图与哈密顿图的关系:
给定完全二部图\(G=\langle V_1,V_2,E \rangle,|V_1| \le |V_2|,|V_1| \ge 2,|V_2| \ge 2.\)有以下结论:
(a) 若\(G\)是哈密顿图，则\(|V_2|=|V_1|.\)
(b) 若\(G\)是半哈密顿图，则\(|V_2|=|V_1|+1\)或\(|V_2|=|V_1|\).
(c) 若\(|V_2| \ge |V_1|+2,\)则\(G\)不是哈密顿图，也不是半哈密顿图.

定理:设\(G\)是\(n\)阶无向简单图，若对于\(G\)中任意不相邻顶点\(u,v,\)均有\(d(u)+d(v) \ge n-1,\)则\(G\)中存在哈密顿通路.
推论: 设\(G\)是\(n\)阶无向简单图，若对于\(G\)中任意不相邻顶点\(u,v,\)均有\(d(u)+d(v) \ge n,\)则\(G\)中存在哈密顿回路.
注:上面两个仅是充分条件，不满足也可能存在哈密顿回路/通路.

定理:设\(u,v\)为\(n\)阶无向简单图\(G\)中两个不相邻的顶点，且\(d(u)+d(v) \ge n,\)则\(G\)为哈密顿图 \(\Leftrightarrow\) \(G \cup (u,v)\)为哈密顿图

定理:\(n\)阶竞赛图\(n \ge 2\)中都有哈密顿通路.

注意:实际做题中，我们应该先用这些条件确认是否不存在哈密顿通路/回路，然后再肉眼找出通路/回路，最后才考虑用条件确认其存在.
注意:正十二面体是哈密顿图.

6.3 最短路问题

\(G=\langle V,E,W \rangle.\)指的是一个带权图，\(W(e)\)指的是边\(e\)的权.
通路\(P\)的所有权之和称作\(P\)的长度，记作\(W(P).\)回路\(C\)的长度记作\(W(C).\)
最短路径、距离的概念(不可达为\(+\infty\)).
最短路问题:使用Dijkstra算法(边权非负)
操作:回想你的代码，大部分是相同的.贴一个完整过程在这里.

中国邮递员问题:本质上就是给定一个带权无向图，每条边的权为非负实数，求每一条边至少经过一次的最短回路.
操作:找出全部的奇度顶点，两两配对找出重复路径最小值，然后答案为全部路径之和加上重复路径之和.

货郎担问题:给定\(G=\langle V,E,W \rangle\)为\(n\)阶完全带权图，各边权非负且可以为\(+\infty\).求\(G\)中一条最短的哈密顿回路.
这个问题至今还没有有效算法，所以我们只能枚举.

一些容易错的题目:
1.给定一个非欧拉图\(G,\)问加几条边才能使其变为欧拉图?
解:加一条边消去\(2\)个奇度顶点，因此一共需要加\(\frac{n}{2}\)条边，\(n\)为奇度顶点的数量.

2.某次国际会议有\(8\)人参加，已知每人至少会与其余\(7\)人中的\(4\)人说相同的语言，问服务员是否将他们安排在同一张圆桌就坐，使得每个人都能与两边的人交谈.
思路:看到圆桌的题目就想到是用哈密顿回路做，而排成一列就是用哈密顿通路做.
证明:由已知条件,\(\forall v \in V,d(v) \ge 4,\)然后由哈密顿回路的判定条件得可以组成哈密顿回路.

3.在\(k\)个长度大于等于3的，彼此分离的圈(都为无向的或者都为有向的)之间至少加多少条新边，才能使所得的图为欧拉图?
答案:\(k\)条边.

4.设\(G\)是恰含\(2k\)个奇度顶点的无向连通图，证明:\(G\)所有的边可以划分为\(k\)条边不重的简单通路\(\Gamma_1,\Gamma_2,\ldots,\Gamma_k,\)使得\(E(G) = \bigcup\limits_{i=1}^{k} E(\Gamma_i)\)
思路:没有思路的题目就试试归纳法吧.
证明:当\(k=1\)时，\(G\)中存在欧拉通路，满足题意.
设\(G\)有\(2k\)个奇度顶点时命题为真，下证有\(2k+2\)个奇度顶点是命题为真.
对于有\(2k+2\)个奇度顶点的图\(G,\)任取其奇度顶点\(u,v,\)令\(G'=G \cup (u,v),\)由归纳假设知\(G' = \bigcup\limits_{i=1}^{k} E(\Gamma_i),\)不妨设\((u,v)\)在\(\Gamma_k\)中,则\(\Gamma_k -(u,v)\)为两条简单通路，于是得证.

5.完全图\(K_n\)都是哈密顿图吗？
思路:这种题要考虑特殊情况.
当\(n=2\)时，不是哈密顿图.其余都是哈密顿图.

6.设\(G\)是无向连通图，证明:若\(G\)中有桥或者割点，则\(G\)不是哈密顿图.
若\(G\)中有割点，则删除这个点后，由哈密顿图的必要条件知，\(G\)不是哈密顿图.
若\(G\)中有桥，设为\(e=(u,v),\)若\(u,v\)为悬挂顶点，则与无向连通图的定义矛盾.若它们至少有一个不是悬挂顶点，删除\(e\)后至少产生\(2\)个连通分支，与哈密顿图的必要条件矛盾，因此不是哈密顿图.

7.证明:设\(u,v\)为\(n\)阶无向简单图\(G\)中两个不相邻的顶点，且\(d(u)+d(v) \ge n,\)则\(G\)为哈密顿图 \(\Leftrightarrow\) \(G \cup (u,v)\)为哈密顿图.
证明:必要性是显然的.
下面证明充分性.
若\((u,v)\)不在\(G \cup (u,v)\)的哈密顿回路中，则命题得证.
若\((u,v)\)在\(G \cup (u,v)\)的哈密顿回路中，设\(G \cup (u,v)\)的一条哈密顿回路\(\Gamma\)为\(uv_2v_3\ldots v_{n-1}v.\)
先证:\(d(u) \ge 2.\)若\(d(u)=1,\)则\(d(u) + d(v) \le 1+(n-2)=n-1.\)矛盾.
于是设\(v_{i_1}v_{i_2}\ldots v_{i_m}\)与\(u\)相邻，下证\(v_{i_1-1},v_{i_2-1}\ldots v_{i_m-1}\)中至少有一个与\(v\)相邻.
若没有一个与\(v\)相邻，则\(d(u) + d(v) \le m+1+(n-2)-m =n-1.\)矛盾.
设\(v_{i_r-1}\)与\(v\)相邻，于是\(uv_2\ldots v_{i_r-1}vv_{n-1}\ldots v_{i_r}u\)为一条哈密顿回路.
示意图如下图所示.

8.今有\(n\)个人，已知他们中任何二人合起来认识其余的\(n-2\)个人.证明:\(n \ge 3\)时，这\(n\)个人能排成一列，使得任何两个相邻的人都相互认识.而当\(n \ge 4\)时，这\(n\)个人能排成一个圆圈，使得每个人都认识两旁的人.
思路；遇到没有办法解决的题，我们要想办法找出一些性质帮助我们做题.
证明:我们任取\(u,v\)这两个人，若\(u,v\)相互认识，则\(d(u)+d(v) \ge n.\)
若\(u,v\)不相互认识，下面证明:\(\forall w \in V,w \not = u \wedge w \not = v,u,v\)认识\(w\).
假设\(w\)不认识\(v\),则对于\(v,w,\)他们均不认识\(u\)，与题目条件矛盾.
于是\(d(u)+d(v) \le 2(n-2).\)
由哈密顿回路(通路)的充分条件，得证.

9.设\(G\)为\(n\)阶无向简单图，边数\(m=\frac{1}{2}(n-1)(n-2)+2,\)证明:\(G\)是哈密顿图,再距离证明\(m=\frac{1}{2}(n-1)(n-2)+1\)时，\(G\)不一定是哈密顿图.
思路:正着证明有时候有困难，那可以尝试反证法.
证明:若\(G\)是哈密顿图，那么对于不相邻的顶点\(u,v,d(u)+d(v) \ge n.\)
若存在不相邻的\(u,v,d(u)+d(v) \le n-1.\)
则考虑\(G'=G-(u,v),G'\)的边数\(m' \ge \frac{1}{2}(n-2)(n-3)+1.\)
又由于\(G'\)为无向简单图，因此\(m' \le \frac{1}{2}(n-2)(n-3)\)
矛盾.于是证毕.
小结论:无向简单图边数最多的时候是完全图.

10.某工厂使用一台设备，每年年初要决定是继续使用，还是购买新的．预计该设备第1年的价格为\(11\)万元，以后每年涨\(1\)万元．使用的第\(1\)年，第\(2\)年，\(\ldots\)，第 \(5\)年的维修费分别为\(5,6,8,11,18\)万元．使用\(1\)年后的残值为\(4\)万元，以后每使用\(1\)年残值减少\(1\)万元．试制定购买维修该设备的\(5\)年计划，使总支出最小.
答案: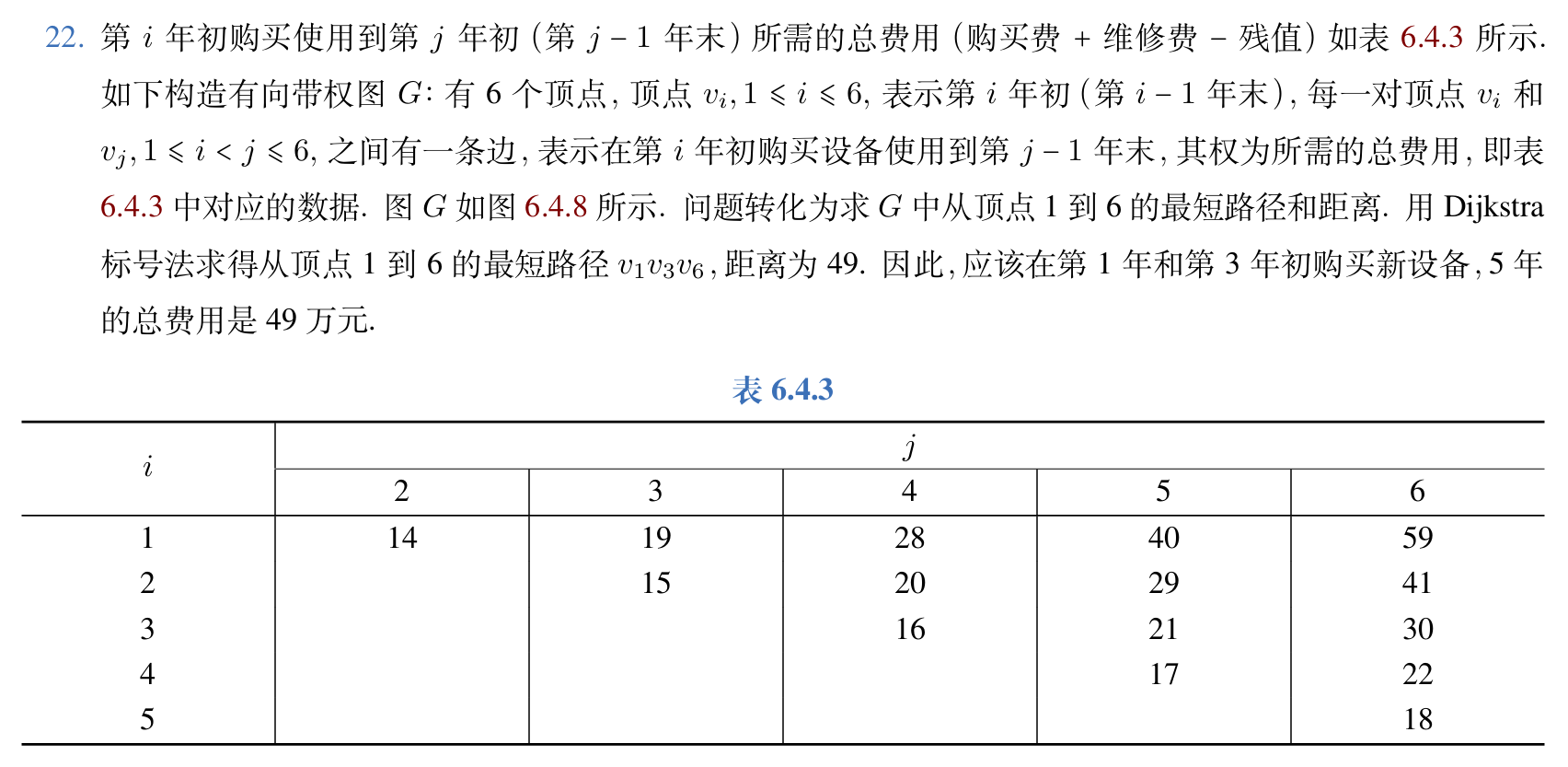

11.设完全二部图\(K_{r,s}\)为哈密顿图，则?
答案:\(r=s \ge 2.\)
注意:大于等于2不能漏.

12.命题:"强连通的有向图都是哈密顿图"是否为真?
答案:否.

13.设\(G\)为无向连通图，\(C\)为\(G\)中一条初级回路.若从\(C\)上删除一条边后，\(C\)上剩下的边构造的路径都是\(G\)中最长的路径.证明:\(C\)为\(G\)中的哈密顿回路.
思路:这道题我们没有办法用哈密顿回路的性质去做，但是注意到初级回路不会经过重复的点和边，于是只需证明所有的点都是\(C\)上，用反证法.
证明:若存在点\(u\)不在\(C\)上，由\(G\)的连通性，任取\(C\)上\(v,u,v\)之间有一条路径\(\Gamma=u\ldots v\),设\(C\)上与\(v\)相邻的顶点为\(w,\)则\(C-(w,v)=\Gamma_2,\)令\(\Gamma_1=u\ldots v +\Gamma_2,\)与\(\Gamma_2\)的最长性矛盾.证毕.

下学期，也请各位继续关注：
《System beats!》
《大二病也要学离散！》
《数算の旅》
《某信息学的概率统计》
还有——

《我的算法竞赛不可能这么可爱》

本期到此结束！