【大二病也要学离散！】第五章 图的基本概念

今天我们正式进入图论部分
话说为啥二十来页就把OI里讲好久的东西讲完了

5.1 图的定义及运算

无序积的定义:设\(A,B\)为任意两个集合，称\(\{\{a,b\} | a \in A,b \in B\}\)为\(A\)与\(B\)的无序积，记作\(A \& B\).将\(\{a,b\}\)简记为\((a,b),\)同时有\(A \& B = B \& A.\)
无向图的定义:\(G= \langle V,E \rangle\)
点集，顶点，边集，无向边(边)
有向图的定义:\(D = \langle V,E \rangle\)
点集，顶点，有向边，边集
用小圆圈表示图的顶点，用顶点之间的连线表示无向边，用带箭头的连线表示有向边.

一些定义:
(1) 有向图和无向图统称为图，有时单独将无向图称作图.有时用\(G\)泛指图，有时则用\(D\)和\(G\)区分，用\(V(G)\)和\(E(G)\)表示点集和边集，\(|V(G)|\)和\(|E(G)|\)表示点数和边数.
(2) 顶点数称为图的阶，\(n\)个顶点的图称为\(n\)阶图.
(3) 零图指一条边都没有的图，\(n\)阶零图称为\(N_n.\)一阶零图称为平凡图.
(4) 虽然顶点集规定为非空集，实际运算时可能产生顶点集为空集的图，称为空图，记作\(\emptyset.\)
(5) 如果给每一个顶点和每一条边指定一个符号，称这样的图为标定图,反之为非标定图.
(6) 将有向图的各条有向边改成无向边后的无向图称为有向图的基图.(注意:重边也要算进去)
(7) 给定无向图\(G=\langle V,E \rangle,e_k =(v_i,v_j) \in E,\)称\(v_i,v_j\)为\(e_k\)的端点，\(e_k\)与\(v_i,v_j\)关联.若这条边不为环，则称\(e_k\)与\(v_i,v_j\)的关联次数为1.否则称\(e_k\)和\(v_i\)的关联次数为2;若不与这条边关联，则称关联次数为0.点相邻:两个点之间有一条边连接，边相邻:两条边有公共顶点.
(8) 给定有向图\(D = \langle V,E \rangle,e_k = \langle v_i,v_j \rangle \in E.\)端点的定义如上，\(v_i\)称为\(e_k\)的始点，\(v_j\)称为\(e_k\)的终点.并且有\(e_k\)与\(v_i,v_j\)关联.若\(v_i=v_j\),称其为环.点相邻:两个点之间有有向边，边相邻:一条边终点是另一条边始点.
图中没有边关联的点称作孤立点.
(9) 给定无向图\(G=\langle V,E \rangle\)和顶点\(v\),与\(v\)相邻且不相等的顶点集合称为它的邻域(\(N_G(v)\)),它的邻域加上\(v\)称为它的闭邻域(\(\overline N_G(v)\))，与\(v\)关联的边的集合称为它的关联集(\(I_G(v)\)).
(10) 给定有向图\(D=\langle V,E \rangle\)和顶点\(v\),与\(v\)相邻且不相等,\(v\)作为始点的点的集合称为它的后继元集(\(\Gamma_D^{+}(v)\)),与\(v\)相邻且不相等,\(v\)作为终点的点的集合称为它的先驱元集(\(\Gamma_D^{-}(v)\)),两者的并集称作它的邻域(\(N_D(v)\)),闭邻域(\(\overline N_D(v)\))的定义同上.
(11) 在无向图中，如果关联一对顶点的无向边多余一条，称其为平行边，它的数量称为重数.有向图的平行边定义相同，只是需要方向相同.含平行边的图称作复杂图，不含平行边和环的图称为简单图.
(12) 设\(G=\langle V,E \rangle,G'=\langle V',E' \rangle,\)若\(V' \subseteq V,E' \subseteq E,\)则\(G'\)为\(G\)的子图，\(G\)为\(G'\)的母图，即\(G' \subseteq G\).若\(V' \subset V \vee E' \subset E,\)则为真子图,\(G' \subset G.\)若\(V' = V,\)称\(G'\)为\(G\)的生成子图.若\(V_1 \subset V \wedge V_1 \not = \emptyset,G\)中两个顶点都在\(V_1\)中组成\(E_1\)的图称为\(G\)的\(V_1\)导出的子图，记作\(G[V_1].\)若\(E_1 \subset E \wedge E_1 \not = \emptyset,E_1\)中关联的顶点作为\(V_1\)的图称为\(G\)的\(E_1\)导出的子图，记作\(G[E_1].\)
(13) 无向图中，删除边，删除顶点，加新边，收缩的定义.它们的符号表示分别为\(G -e,G - V',G \cup (u,v),G \backslash e\).收缩的含义:在\(G\)中删除\(e\)后，将\(e\)的两个端点用\(w\)代替(可以是两个端点其中之一)，并使\(w\)关联除\(e\)外这两个端点关联的所有边.注意:在收缩和加新边过程中可能产生环和平行边.
(14) 设\(G_1=\langle V_1,E_1 \rangle\)和\(G_2 = \langle V_2,E_2 \rangle\)为不含孤立点的两个图，且有向无向性相同.
(a) 称以\(V_1 \cup V_2\)为顶点集，\(E_1 \cup E_2\)为边集的图为\(G_1\)和\(G_2\)的并图,记作\(G_1 \cup G_2.\)
(b) 称以\(E_1 - E_2\)为边集，以\(E_1 - E_2\)中边关联的顶点组成的集合的图为\(G_1\)和\(G_2\)的差图,记作\(G_1 - G_2.\)
(c) 称以\(E_1 \cap E_2\)为边集，以\(E_1 \cap E_2\)中边关联的顶点组成的集合的图为\(G_1\)和\(G_2\)的交图，记作\(G_1 \cap G_2.\)
(d) 称以\(E_1 \oplus E_2\)为边集，以\(E_1 \oplus E_2\)中边关联的顶点组成的集合的图为\(G_1\)和\(G_2\)的环和,记为\(G_1 \oplus G_2.\)
注意:以上所有的定义都基于边集的运算展开
注意:若\(V_1 \cap V_2 = \emptyset,\)则\(G_1\)与\(G_2\)是不交的.若\(E_1 \cap E_2 = \emptyset,\)则\(G_1\)和\(G_2\)是边不交的.不交可推出边不交.
注意:\(G_1 \oplus G_2=(G_1 \cup G_2) - (G_1 \cap G_2).\)
注意:OI中所说的"环"实际上指的是环和圈的统称，离散中讲到环只可能是自环.
注意:正则图一定是简单图.

5.2 度数、通路和回路

下面是一些定义:
(1) 无向图的度数\(d(v),\)有向图的入度\(d_{-}(v),\)出度\(d_{+}(v),\)度数\(d(v).\)无向图的最大度数\(\Delta(G),\)最小度数\(\delta(G),\)有向图的最大出度\(\Delta^{+}(D),\)最小出度\(\delta^{+}(v),\)最大入度\(\Delta^{-}(v),\)最小入度\(\delta^{-}(v),\)最大度数\(\Delta(v),\)最小度数\(\delta(v).\)度数为1的顶点为悬挂顶点,与它关联的边称为悬挂边,奇度顶点和偶度顶点的定义.
注意:环提供2个度数.
(2) 握手定理:任何无向图中,所有顶点的度数之和为边数的2倍.任何有向图中，所有顶点的度数之和为边数的2倍,所有顶点的入度之和等于所有顶点的出度之和,都等于边数.
推论:任何图中，奇度顶点的个数是偶数.
(3) 设\(G=\langle V,E \rangle\)为一个无向图,\(V=\{v_1,v_2,\ldots,v_n\},\)称\(d=(v_1),d(v_2),\ldots,d(v_n)\)为\(G\)的度数列，对于顶点标定的无向图，它的度数列是唯一的.反之，对于给定的非负整数列\(d=(d_1,d_2,\ldots,d_n),\)其可图化或可简单图化.有向图还可定义入度列或者出度列.
定理:非负整数列\(d=(d_1,d_2,\ldots,d_n)\)可图化 \(\Leftrightarrow\) \(\sum\limits_{i=1}^{n}d_i\)是偶数.
定理:\(G\)为任意\(n\)阶无向简单图，则\(\Delta(G) \le n-1.\)
注意:判断是否可简单图化,上面的只是必要条件，实际还要自己画画看.
(4) 设\(G_1=\langle V_1,E_1 \rangle\)和\(G_2 = \langle V_2,E_2 \rangle\)是两个无向图，若存在双射\(f:V_1 \rightarrow V_2,\forall v_i,v_j \in V_1,(v_i,v_j) \in E_1 \Leftrightarrow (f(v_1),f(v_2)) \in E_2,\)并且这两条边的重数相同，则称\(G_1\)和\(G_2\)同构,记作\(G_1 \cong G_2\).对有向图，只需额外考虑边的方向.
注意:至今还没有找到两个图同构的充要条件,阶数相同、边数相同、度数列相同等都是必要条件.
(5) \(G\)为\(n\)阶无向简单图，若顶点两两相邻，则\(G\)为\(n\)阶无向完全图，简称\(n\)阶完全图,记作\(K_n\).
\(D\)为\(n\)阶有向简单图，若每个顶点都邻接到其他顶点，则称\(D\)为\(n\)阶有向完全图.
\(G\)为\(n\)阶有向简单图，若其基图为\(K_n,\)称其为\(n\)阶竞赛图.
它们的边数分别为:\(\frac{n(n-1)}{2},n(n-1),\frac{n(n-1)}{2}.\)
(6) 设\(G\)为\(n\)阶无向简单图，若\(\forall v \in V(G),d(v)=k,\)称\(G\)为\(k-\)正则图,边数\(\frac{kn}{2}.\)
注意:彼得松图是10个点，15条边的3-正则图.
注意:画出所有非同构的简单图时，注意先枚举度数列。
注意:构造所有非同构的\(n\)阶\(m\)条边的简单图至今还未解决.
(7) 设\(G=\langle V,E \rangle\)是\(n\)阶无向简单图,\(\overline{E}=\{(u,v) | u,v \in V,u \not = v,(u,v) \notin E\}, \overline{G}=\langle V,\overline{E} \rangle\)是\(G\)的补图,若\(G \cong \overline{G},\)则\(G\)为自补图.
(8) 设\(G\)为无向标定图，顶点与边的交替序列\(\Gamma=v_{i_0}e_{j_1}v_{i_1}\ldots e_{j_l}v_{i_l}\)称作从\(v_{i_0}\)到\(v_{i_l}\)的通路，始点和终点的定义是显然的，边的条数称作长度.回路的定义也是显然的.若所有边互不相同,则为简单通路(回路).若所有顶点(除\(v_{i_0}\)和\(v_{i_l}\))互不相同，所有边都互不相同,则称为初级通路(路径)/初级回路(圈)，奇圈和偶圈随长度而定.在简单无向图中，圈的长度至少为3.有向图中也有类似定义.另外,初级通路(回路)必然是简单通路(回路).
定理:在\(n\)阶图\(G\)中，若从\(u\)到\(v\)存在通路，且\(u \not = v,\)则存在从\(u\)到\(v\)且长度小于等于\(n-1\)的通路 \(\Rightarrow\) 初级通路.
定理:在\(n\)阶图\(G\)中，若存在\(v\)到自身的回路，则一定存在\(v\)到自身长度小于等于\(n\)的回路 \(\Rightarrow\) 初级回路.
回路的意义:同构意义下长度相同的圈只有一个，标定图中定义意义下序列不同即不同，有时候也要看是否考虑顺时针逆时针差异.

5.3 图的连通性

下面是一些定义:
(1) 无向图\(G = \langle V,E \rangle ,\)若\(u\)和\(v\)之间存在通路,称\(u\)和\(v\)是联通的，记作\(u \sim v\),注意\(\forall v \in V,v \sim v,\)它是一种等价关系.
若\(G\)是平凡图或者任意顶点都是连通的，则称其为连通图，反之称为非连通图.
注意: 当\(n \ge 1,K_n\)都是连通图，当\(n \le 2,N_n\)都是非连通图.
(2) 设\(G=\langle V,E \rangle,\)G的一个连通块\(G[v_i]\)(即关于"连通"这个等价关系的一个等价类)称为它的一个连通分支.\(G\)的连通分支数称为\(p(G).\)
注意:连通图的\(p(G)=1,\)非连通图的\(p(G) \ge 2,N_n\)的\(p(G)\)是最大的，为\(n\).
(3) 任取两个顶点\(u,v,\)若\(u \sim v,\)称最短通路为它们之间的短程线,其长度称为它们之间的距离，记为\(d(u,v).\)若不连通，则\(d(u,v) = + \infty.\)
关于距离的性质:
(a) \(d(u,v) \ge 0, d(u,v)=0 \Leftrightarrow d(u,v)=0.\)
(b) \(d(u,v)=d(v,u)\)
(c) \(d(u,v)+d(v,w) \ge d(u,w)\)
注意:顶点可以来表示实际问题中的状态，从而解决实际生活中的问题.
(4) 设无向图\(G=\langle V,E \rangle,\)若存在\(V' \subset V,p(G-V')>p(G),\)且\(\forall V'' \subset V',p(G-V'')=p(G),\)称\(V'\)为\(G\)的点割集(或割点)
设无向图\(G=\langle V,E \rangle,\)若存在\(E' \subset E,p(G-E')>p(G),\)且\(\forall E'' \subset E',p(G-E'')=p(G),\)称\(E'\)为\(G\)的边割集(或割边(桥))
注意:割点的度数必然大于等于\(2\),如果\(n \ge 3,\)桥的两个端点中必然有一个度数$ \ge 2,\(并且它是**割点**. (5) 若\)G\(是无向连通图且**不是完全图**,则最小点割集的大小称为\)G\(的点连通度，简称**连通度**,记为\)\kappa(G)\(.我们规定,**完全图**的连通度为**n-1**,**非完全图**的连通度为**0**.若\)\kappa(G) \ge k,\(则称\)G\(为\)k-\(连通图(**注意**:一张图的\)k\(可能不是唯一的.)，它的意义是，删除任意\)k-1\(个顶点，得到的图一定还是连通的. 若\)G\(是无向连通图,则最小边割集的大小称为\)G\(的**边连通度**，,记为\)\lambda(G)\(.我们规定,**非完全图**的边连通度为**0**.若\)\lambda(G) \ge r,\(则称\)G\(为\)r-\(边连通图(**注意**:一张图的\)r\(可能不是唯一的.),它的意义是，删除任意\)r-1\(条边，得到的图一定还是连通的. 比较点连通程度和边连通程度，还是比较\)\kappa(G)\(和\)\lambda(G)\(哪个大. **小技巧**:计算连通度的时候，可以先针对每个顶点，看这个顶点相邻的顶点数或者关联的边数. 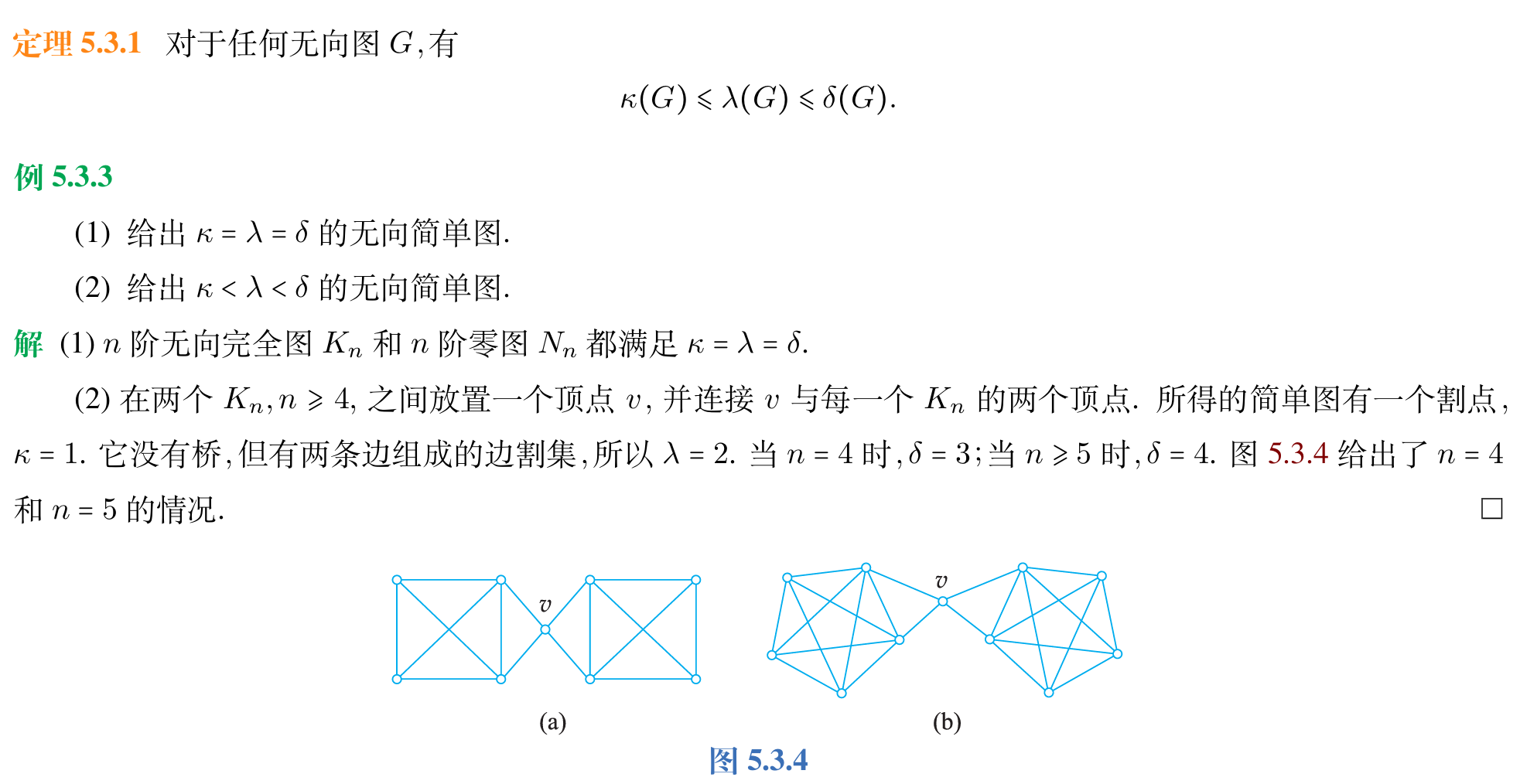定理:对任何无向图\)G\(,有\)\kappa(G) \le \lambda(G) \le \delta(G).\( 一个小例子:  (6) 给定有向图\)D=\langle V,E \rangle,v_i,v_j,\(若存在\)v_i\(到\)v_j\(的通路，称\)v_i\(**可达**\)v_j\(,记作\)v_i \rightarrow v_j.\(注意\)\forall v_i \in V,v_i \rightarrow v_i.\(若\)v_i \rightarrow v_j \wedge v_j \rightarrow v_i,\(称它们**相互可达**,记作\)v_i \leftrightarrow v_j.\( **注意**:可达和相互可达都是二元关系，相互可达是**等价关系**. 短程线和距离的定义同无向图，只要求可达，不要求相互可达. 距离除了**对称性**，具有全部无向图中距离具有的性质. (7) 若有向图的**基图**是连通图,称其为**弱连通图**,简称为**连通图**;若\)\forall v_i,v_j \in V,v_i \rightarrow v_j \vee v_j \rightarrow v_i,\(称其为**单向连通图**;若\)\forall v_i,v_j \in V,v_i \leftrightarrow v_j,$称其为强连通图.
注意:强连通图一定是单向连通图,单向连通图一定是弱连通图.
强连通图 \(\Leftrightarrow\) 存在经过每个顶点至少一次的回路
单向连通图 \(\Leftrightarrow\) 存在经过每个顶点至少一次的通路
(8) 一种常用于路径和圈的构造性证明的方法:扩大路径法.若路径\(\Gamma\)的始点和终点都不与\(\Gamma\)外的顶点相邻，则称其为一条极大路径.给定一条路径，一直延伸始点和终点的相邻顶点，直到不能再延伸了，得到一条极大路径.
下面是扩大路径法的一个例子:

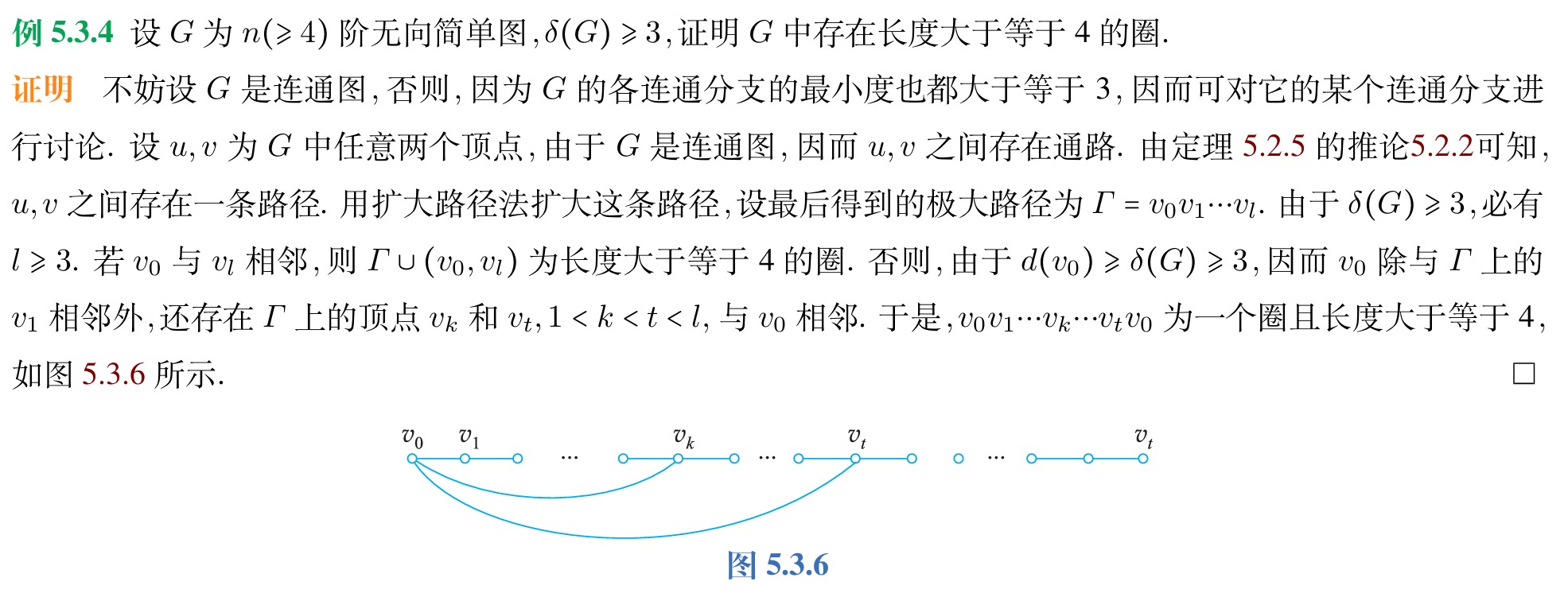
题目中的另一个小技巧:假设是连通图，否则对它的某个连通分支进行讨论.
(9) 设无向图\(G=\langle V,E \rangle,\)若能将\(V\)划分为\(V_1,V_2,V_1 \cap V_2 = \emptyset,V_1 \not = \emptyset,V_2 \not = \emptyset,\)使得\(G\)中的每条边的两个端点都是一个属于\(V_1,\)一个属于\(V_2,\)则称\(G\)为二部图(二分图、偶图),称\(V_1\)和\(V_2\)为互补顶点子集，常将其记作\(\langle V_1,V_2,E \rangle.\)若\(G\)是简单二部图,且\(V_1\)的每个顶点均与\(V_2\)中的每个顶点相邻，称其为完全二部图,记为\(K_{r,s},r=|V_1|,s=|V_2|.\)
注意:\(n \ge 2,N_n\)为二部图.
画二部图时，人们习惯将\(V_1,V_2\)分开画成两排.
判定二部图的定理: \(n \ge 2,n\)阶无向图\(G\)是二部图 \(\Leftrightarrow\) \(G\)中无奇圈.
证明可以多看看.

5.4 图的矩阵表示

(1) 设无向图\(G=\langle V,E \rangle,V=\{v_1,v_2,\ldots,v_n\},E=\{e_1,e_2,\ldots,e_m\},\)令\(m_{ij}\)为\(v_i\)与\(e_j\)的关联次数,则称\((m_{ij})_{n \times m}\)为\(G\)的关联矩阵，记作\(\mathbf{M}(G).\)
其有以下性质:
(a) 每列元素之和都为2
(b) 第\(i\)行元素之和为\(v_i\)的度数
(c) 整个矩阵的元素之和是边数2倍
(d) 第\(j\)列和第\(k\)列相同 \(\Leftrightarrow\) \(e_j\)和\(e_k\)是平行边
(e) 第\(i\)行元素之和为0当且仅当\(v_i\)是孤立点
(2) 给定有向无环图\(D,\)令\(m_{ij}=1\)(\(v_i\)为\(e_j\)始点),\(m_{ij}=-1\)(\(v_i\)为\(e_j\)终点),\(m_{ij}=0\)(\(v_i\)与\(e_j\)不关联).则称\((m_{ij})_{n \times m}\)为\(D\)的关联矩阵，记作\(\mathbf{M}(D).\)
其有以下性质:
(a) 每一列恰有一个1和一个-1
(b) -1的个数等于1的个数，都等于边数(握手定理)
(c) 在第\(i\)行中，1的个数等于\(d^{+}(v_i)\),-1的个数等于\(d^{-}(v_i).\)
(d) 平行边对应的列相同.
(3) 给定有向图\(D=\langle V,E \rangle,\)令\(a_{ij}^{(1)}\)为从顶点\(v_i\)邻接到\(v_j\)的边的条数，称\((a_{ij}^{(1)})_{n \times n}\)为\(D\)的邻接矩阵，记作\(\mathbf{A}(D)\),简记为\(\mathbf{A}.\)
其有以下性质:
(a) 第\(i\)行之和为\(d^{+}(v_i)\)
(b) 第\(j\)列之和为\(d^{-}(v_j)\)
(c) 整个矩阵之和为边数\(m\)
(4) 设\(\mathbf{A}\)为\(D\)的邻接矩阵，则\(\mathbf{a}^l\)中元素\(a_{ij}^{(l)}\)表示\(D\)中\(v_i\)到\(v_j\)长度为\(l\)的通路数,\(a_{ii}^{(l)}\)表示\(v_i\)到自身长度为\(l\)的回路数，\(\mathbf{A}^l\)整个矩阵之和为\(D\)中长度为\(l\)的通路(含回路)总数，对角线元素之和为\(D\)中长度为\(l\)的回路总数.
若\(l \ge 1,B_l=\mathbf{A}+\mathbf{A}^2+\ldots +\mathbf{A}^l,\)则\(B_l\)元素之和为\(D\)中长度小于等于\(l\)的通路(含回路)总数，对角线元素之和为\(D\)中长度小于等于\(l\)的回路总数.
(5) 给定有向图\(D\),令\(p_{ij}=1,v_i \rightarrow v_j,\)否则为0.称\((p_{ij})_{n \times n}\)为\(D\)的可达矩阵，记作\(\mathbf{P}(D)\),简记为\(P.\)
其主对角线上元素均为1.
只要计算出\(B_{n-1},\)通过它的元素是否为0可以写出可达矩阵,但是主对角元元素与\(B_{n-1}\)无关.
(6) 写出无向图的邻接矩阵和可达矩阵，只需要把无向边看做方向相反的有向边(自环只看作一条边),注意它的邻接矩阵和可达矩阵都是对称的.

下面是一些比较容易错的题目:
1.已知无向图\(G\)的边数\(m=10,3\)个\(2\)度顶点，\(2\)个\(4\)度顶点，其余顶点都是奇度顶点，试讨论奇度顶点的个数以及度数分配情况.
解:剩余顶点的度数之和为\(6,\)我们进行以下拆分.
\(6=1+1+1+1+1+1\)
\(6=3+1+1+1\)
\(6=3+3\)
\(6=5+1\)
共四种情况.

2.讨论\(K_5\)和\(K_6\)各有几个非同构的生成子图为正则图.
思路：先回顾一下定义，生成子图是指点集和母图一样的子图，同时正则图的\(kn\)一定要是偶数.
解:对于\(K_5,\)可以取它的\(2-\)正则图，\(4-\)正则图,\(0-\)正则图.共3个
对于\(K_6,\)可以取它的\(0-\)正则图，\(1-\)正则图，\(2-\)正则图，\(3-\)正则图，\(4-\)正则图,\(5-\)正则图.共6种.

3.小提示:正则图的补图也是正则图.
小提示:\(k-\)连通图，给定\(k\)，不能确定\(\kappa(G).\)
小提示:给定无向图，既有割点又有桥，并不能确定\(\delta(G).\)
小提示:非完全无向图中，极大路径不一定是最长路径.

4.单向连通图中最多加1条边就能成为强连通图.

5.在无向完全图\(K_{n},n \ge 2\)中寻找边数最多的生成子图，使其成为完全二部图\(K_{r,s}.\)
思路:这里需要注意完全二部图的边数:\(m=rs.\)
解:\(n\)为偶数时，\(rs=\frac{n^2}{2}.\)
\(n\)为奇数时，\(rs=\frac{n^2-1}{4}.\)

6.设\(r \ge 1,s \ge 1,\)则由完全二部图\(K_{r,s}\)产生完全图\(K_{r+s}\)需要添加多少条边？
解:直接计算 需要添加\(\frac{(r+s)(r+s-1)}{2}-rs=\frac{r^2-r+s^2-s}{2}\)条边.

7.注意:看到非同构就要判断它是同构意义下的，只看长度.

8.画出度数列为\((2,2,2,2,3,3)\)的非同构的简单图.
答案: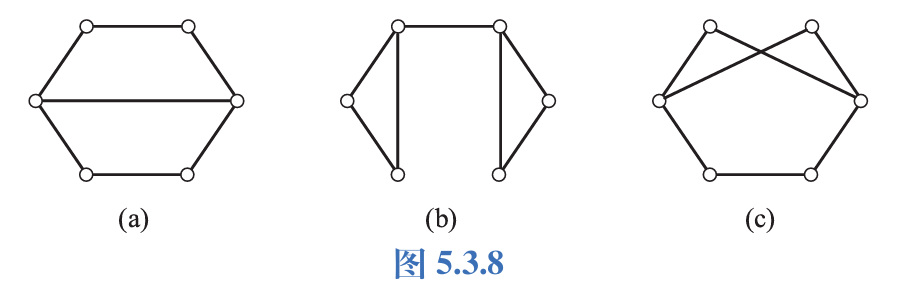

9.证明:三维空间中不存在有奇数个面且每个面都有奇数条棱的多面体.
思路:这道题其实是我们用图论知识解决实际问题的范例.
解:设\(v_i\)表示这个多面体面\(i,i\)和\(j\)有公共棱 \(\Leftrightarrow\) 面\(i\)和\(j\)相邻.
于是有图\(G\)的点数为奇数，每个点的度数为奇数，由于度数之和应为边数的2倍，矛盾.

10.最大度和最小度都等于\(2\)的\(6\)阶无向图有几种非同构情况？其中有几种是简单图?
答案:

11.画出\(3\)阶有向完全图的所有非同构的子图，指出哪些是生成子图，并指出哪些是\(3\)阶竞赛图.
答案: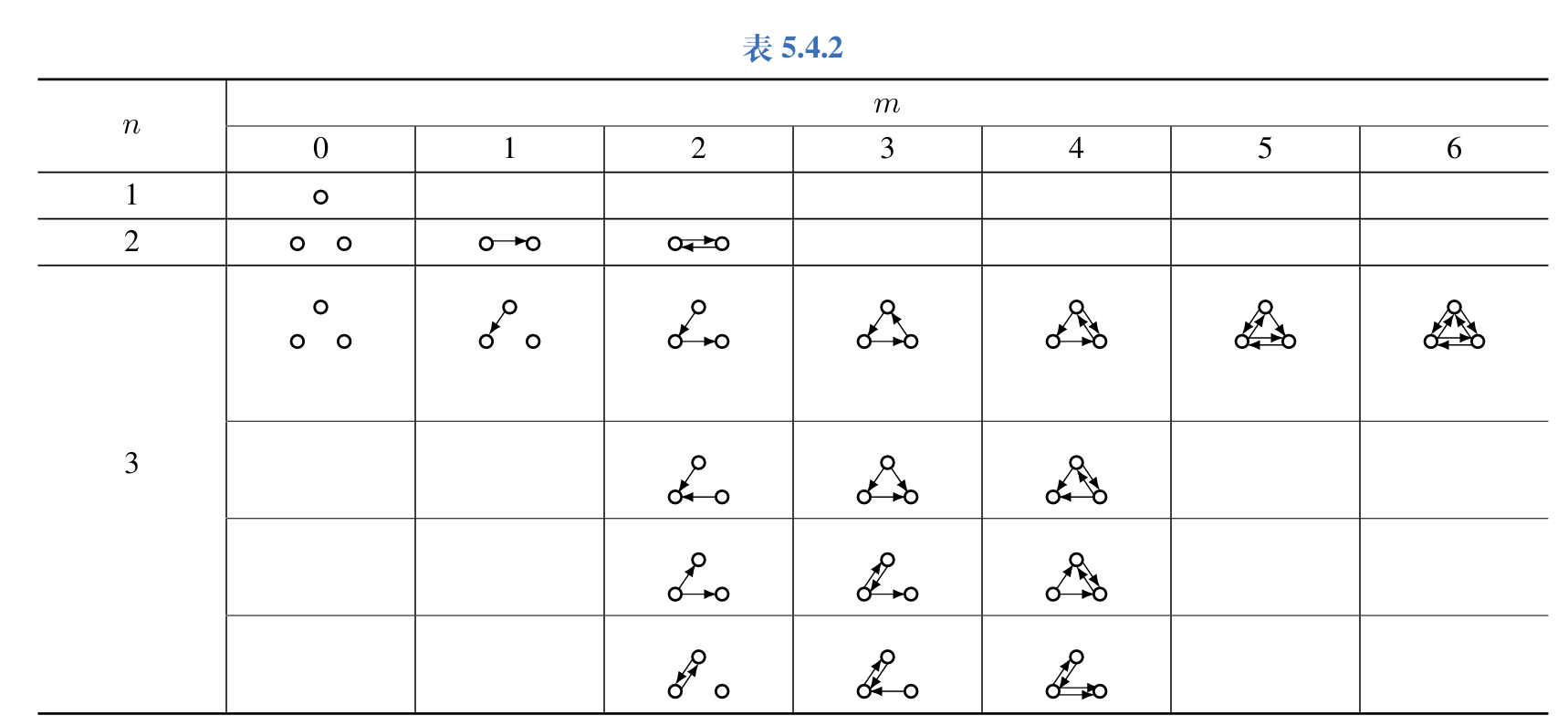

12.小结论:\(n\)阶自补图满足以下性质:\(n \equiv 0(\mathrm{mod} \ 4) \vee n \equiv 1(\mathrm{mod} \ 4).\)

13.画出\(5\)阶\(7\)条边的所有非同构的无向简单图.
小技巧:要画出这种图，我们可以考虑它的补图.
于是转化为画\(5\)阶\(3\)条边的所有非同构的无向简单图.
放一个答案在这里

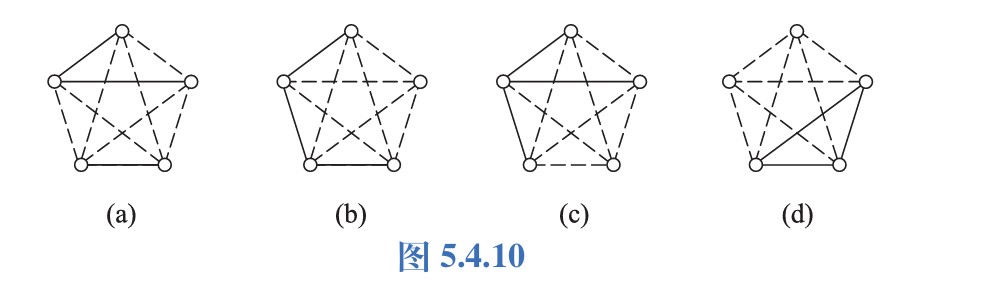
14.小结论:设\(G_1\)和\(G_2\)均为无向简单图，\(\overline{G_1}\)和\(\overline{G_2}\)分别是\(G_1\)和\(G_2\)的补图.证明:\(G_1 \cong G_2 \Leftrightarrow \overline{G_1} \cong \overline{G_2}\)

15.\(6\)阶\(2-\)正则图有几种非同构的情况？
答案:就两种，一种是长度为\(6\)的圈，另一种是\(2\)个长度为\(3\)的圈
再次强调:正则图是简单图.

16.设\(e=\langle u,v \rangle\)是无向图\(G\)中的一条边，证明:\(e\)为桥当且仅当\(e\)不在任何圈中.
思路:本题应该结合割边的定义进行证明,考虑使用反证法.
证明:必要性:设\(e\)在某个圈\(uv_1v_2\ldots v\)中，则\(P(G - e)=P(G),\)与\(e\)为桥矛盾，因此必要性成立.
充分性:设\(e\)不是桥，则在\(G - e\)中\(u\)和\(v\)仍然连通，设通路为\(uv_1v_2\ldots v,\)于是\(uv_1v_2\ldots vu\)为一个圈，与\(e\)不在任何圈中矛盾，于是充分性成立.

17.\(e=(u,v)\)为无向图\(G\)中的桥，证明:\(u\)是割点当且仅当\(u\)不是悬挂顶点.
思路:还是结合割边和割点的定义进行证明
必要性:假设\(u\)是割点且\(u\)为悬挂顶点，此时\(P(G - u)=P(G),\)不符合割点定义，矛盾，必要性成立.
充分性:若\(u\)不是悬挂顶点，则除\(v\)之外还有\(u_1u_2\ldots u_n\)与\(u\)相连，且删除\(e\)后两者属于不同连通分支，于是删除\(u\)后仍然属于不同连通分支，因此\(u\)为割点.

18.设\(n \ge 2,\)证明:\(n\)阶简单连通图\(G\)中至少有两个顶点不是割点.
证明:这道题超纲了，学了下一章再来:)

19.小结论:
当\(n \ge 4\)时，无向完全图\(K_n\)中有\(\lfloor \frac{n}{2} \rfloor -1\)种非同构的偶圈.
当\(n \ge 2\)时，\(n\)阶有向完全图中有\(n-1\)非同构的圈.
当\(n \ge 3\)时，\(n\)阶竞赛图中最多了\(n-1\)非同构的圈.

20.若无向图\(G\)中恰有两个奇度顶点，证明这两个奇度顶点必然连通.
思路:怎么利用奇度顶点的性质？我们的思路应该很清晰，讲到度数首先要想到握手定理.
证明:假设这两个奇度顶点不连通，则它们分别位于不同的连通分支中，考虑这两个连通分支各自作为图，则其中只含一个奇度顶点，与握手定理矛盾.

21.设\(G\)是无向简单图，\(\delta(G) \ge 2,\)证明:\(G\)中存在长度大于等于\(\delta(G)+1\)的圈.
思路:这题肯定是极大路径法，下面展示一下极大路径法的书写格式.
证明:不妨设\(G\)为连通图，否则因为各连通分支的最小度大于等于2，可以对它的某个连通分支进行讨论.设\(u,v\)为\(G\)中任意两个顶点，由于\(G\)为连通图，因此\(u,v\)之间存在通路，进而知道其之间存在一条路径.用扩大路径法扩大，得到一条极大路径\(v_0v_1\ldots v_l.\)且有\(l \ge \delta(G).\)若\(v_0\)与\(v_l\)相邻，则这条路径并上\((v_l,v_0)\)即为长度大于等于\(\delta(G)+1\)的圈.若否，则路径中存在顶点\(v_{i_1}\ldots v_P{i_\delta(G)}\)与\(v_0\)相邻，它们可以组成一个圈.

练手题:设\(D=\langle V,E \rangle\)为有向简单图,\(\delta(D) \ge 2,\delta^{-}(D)>0,\delta^{+}(D)>0,\)证明:\(D\)中存在长度大于等于\(\mathrm{max}\{\delta^{+}(D),\delta^{-}(D) \}+1\)的圈.

21.设\(2 \ge r \ge s,\)在完全二部图\(K_{r,s}\)中:
(1) 有多少种非同构的圈？
(2) 至多有多少个顶点彼此不相邻？
(3) 至多有多少条边彼此不相邻？
(4) 点连通度\(\kappa\)是多少？边连通度\(\lambda\)是多少？
思路:自己画个图看看
我们给出结论:
(1) 有\(r-1\)种非同构的圈，长度分别为\(4,6,\ldots,2r\).
(2) 至多有\(s\)个顶点互相不相邻.
(3) 至多有\(r\)个顶点互相不相邻.
(4) \(\kappa=\lambda=r\)

22.设\(G\)是\(n\)阶\(m\)条边的无向连通图，证明:\(m \ge n-1.\)
思路:其实这道题就是生成树的基本结论，我们这里用归纳法证明。
放一个答案在下面

23.设\(G\)是\(6\)阶无向简单图，证明:\(G\)或它的补图\(\overline{G}\)中存在\(3\)个顶点彼此相邻.
思路:考虑补图和图的关系？
证明:我们考虑顶点\(v_1,\)它在\(G\)和\(\overline{G}\)中必然存在度数$ \ge 3\(的情况，考虑与\)v_1\(相邻的\)v_2,v_3,v_4.\(若\)v_2,v_3,v_4$有相邻的，则存在\(3\)个顶点彼此相邻.若无，则在目前图的补图中，\(v_2,v_3,v_4\)彼此相邻，得证.

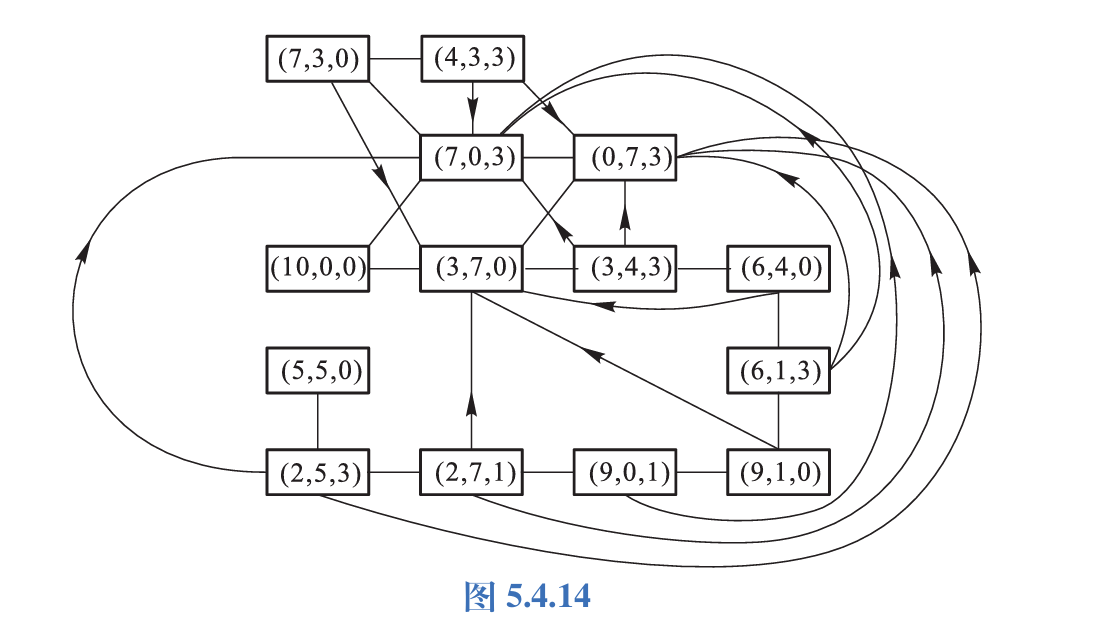
24.有\(3\)个油瓶，分别可装\(500g,350g\)和\(150g\)油，其中\(500g\)装油瓶内装满了油，另两个油瓶是空瓶，如何用这\(3\)个油瓶把这\(500g\)油分成两个\(250g\)？至少要倒多少次？
放一个答案在这

25.\(3\)阶\(3\)条边的有向简单图有()个？
答案:3

26.小结论:若无向连通图\(G\)中没有\(1\)度顶点，则其中必有长度大于等于\(3\)的圈.证明可以用扩大路径法.

下学期，也请各位继续关注：
《System beats!》
《大二病也要学离散！》
《数算の旅》
《某信息学的概率统计》
还有——

《我的算法竞赛不可能这么可爱》

本期到此结束！