【大二病也要学离散！】第二章二元关系

2.1 有序对与笛卡尔积

有序对的概念

笛卡尔积的概念

一般来说，笛卡尔积不满足交换律和结合律。

笛卡尔积的性质

$ A \times \emptyset = \emptyset, \ \emptyset \times A = \emptyset$
左右交换律
- $A \times (B \cup C) = (A \times B) \cup (A \times C)$
- $(B \cup C) \times A = (B \times A) \cup (C \times A)$
- $A \times (B \cap C) = (A \times B) \cap (A \times C) $
- $(B \times C) \cap A = (B \times A) \cap (C \times A) $
若$A \subseteq C,B \subseteq D,$则$A \times B \subseteq C \times D$。
注意:多个笛卡尔积运算时，如果运算中存在括号，那么需要进行元组嵌套，否则答案用平级多元组代替。

2.2 二元关系

二元关系的定义与性质

元素均为有序对的非空集合或者空集。
对于集合$A,B$,$A \times B$的所有子集都是从A到B的二元关系，当$A=B$时，称为A上的二元关系。
$xRy$与$x \not \mathrel{R} y$的关系。
若$|A|=n$，则$|P(A \times A)|=2^{n^2}$。

特殊的二元关系

空集被称为A上的空关系。
$A$上的全域关系和恒等关系
- $E_A=\{\langle x,y \rangle | x \in A \land y \in A\}$
- $I_A=\{\langle x,x \rangle | x \in A \}$
小于或等于关系
整除关系
包含关系

表示二元关系的常见方法

集合表达式
关系矩阵(类似邻接矩阵)
关系图(有关系就连边)

2.3 关系的运算

二元关系的运算规律

(1)
- $(F^{-1})^{-1} =F$
- $\mathrm{dom} (F^{-1}) = \mathrm{ran} F$
- $\mathrm{ran} (F^{-1}) = \mathrm{dom} F$
(2)
- $(F \circ G) \circ H = F \circ (G \circ H)$
- $(F \circ G)^{-1} = G^{-1} \circ F^{-1}$
(3)
- $ R \circ I_A = R = I_A \circ R$
(4)
- $F \circ (G \cup H) = F \circ G \cup F \circ H$
- $(G \cup H) \circ F = (G \circ F) \cup (H \circ F)$
- $F \circ (G \cap H) = F \circ G \cap F \circ H$
- $(G \cap H) \circ F = (G \circ F) \cap (H \circ F)$
- 这个对于有限多个二元关系也成立。
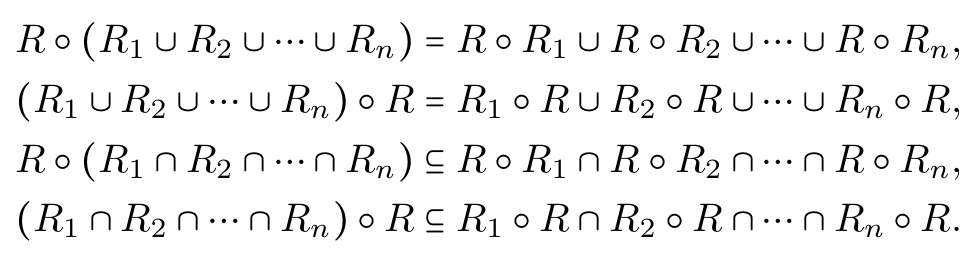
(5)
- $F \upharpoonright (A \cup B) = F \upharpoonright A \cup F \upharpoonright B$
- $F[A \cup B] = F[A] \cup F[B]$
- $F \upharpoonright (A \cap B) = F \upharpoonright A \cap F \upharpoonright B$
- $F[A \cap B] \subseteq F[A] \cap F[B]$

$R$的次幂的定义

注意零次是恒等关系。
其次幂的加法、乘法运算与数域中的相同。
矩阵运算加法是逻辑加，即计算机中的并运算。
一定存在不相等的自然数，使得$R$的两个次幂相等。

$R$次幂的性质

设$R$是$A$上的关系，若存在自然数$s,t,s<t,$使得$R^{s}=R^{t},$则

对任何$k \in N$有$R^{s+k} = R^{t+k}$。
对任何$k,i \in N$有$R^{s+kp+i} = R^{s+i}$ 其中$p=t-s$。
对$S=\{R^{0},R^{1},\ldots,R^{t-1}\},$则对于任意的$q \in N$有$R^{q} \in S$。

2.4 关系的性质

关系的性质

自反
反自反
对称
反对称
传递
注意: 若前提条件不存在，那么仍然能称为对应的关系。
注意: 对称与反对称并不是一定具有其中之一的，但是可以同时具有或者同时不具有。
注意: 在判断传递性的时候，回路节点的自环也要考虑进去。

性质成立的充要条件

自反:$I_A \subseteq R$
反自反:$I_A \cap R = \emptyset$
对称：$R = R^{-1}$
反对称:$R \cap R^{-1} \subseteq I_A$
传递: $R \circ R \subseteq R$

集合运算与性质的关系

若$R_1,R_2$是自反(对称)的，那么$R_1 \cup R_2$是自反(对称)的。
若$R_1,R_2$是传递的，那么$R_1 \cap R_2$是传递的。

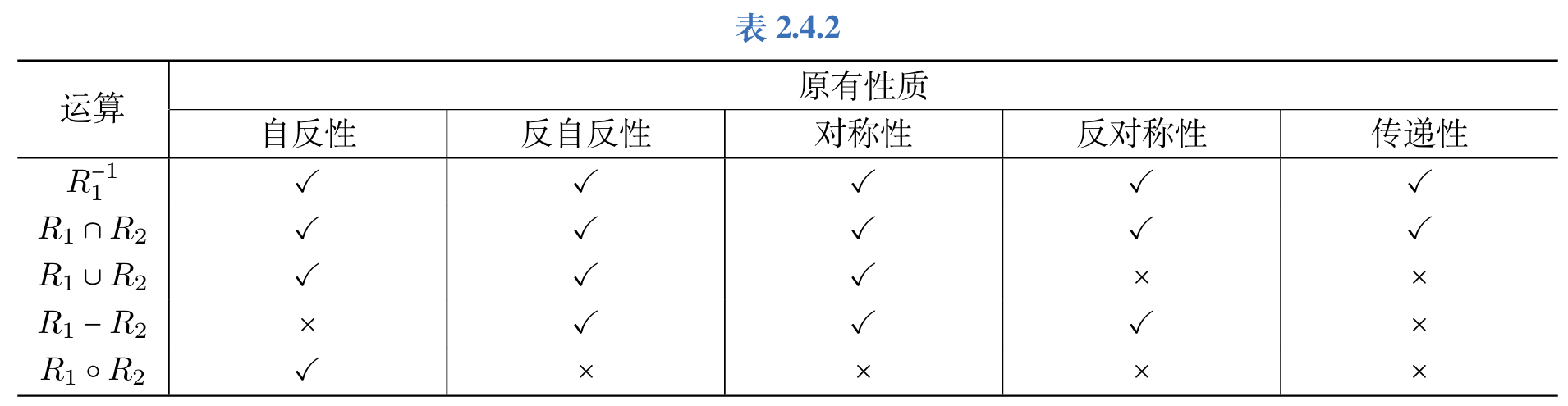
性质在不同表示法下的性质

alt text

集合运算的相关性质

alt text

2.5 关系的闭包

闭包的三个条件

性质
包含
最小性

闭包的计算

$r(R) = R \cup R_{0}$
$s(R) = R \cup R_{-1}$
$t(R) = R \cup R_{2} \cup R_{3} \ldots$
若$R$是有穷集$A$上的关系，则存在自然数$r$使得$t(R) = R \cup R_{2} \cup \ldots R^{r}$。

关系矩阵与关系图求闭包:

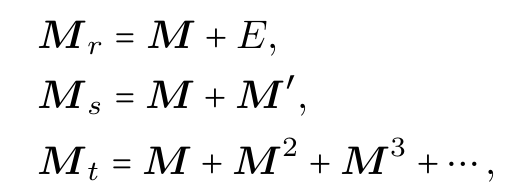
alt text

注意: 关系矩阵使用的是逻辑加。
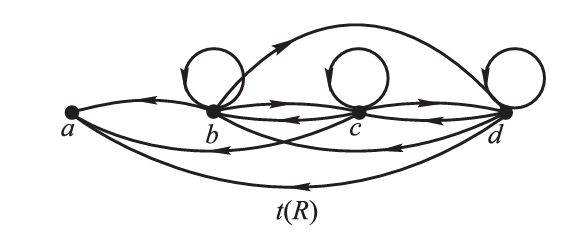
注意: 如果图中存在回路，在画$t(R)$时这条路径上每个点都要加上一个环。

计算机求传递闭包

沃舍尔算法(即OI中Floyd求传递闭包)。

闭包的主要性质:

(1) 若$R$是非空集合$A$上的关系，则

$R$是自反的 $\Leftrightarrow$ $r(R)=R$。
$R$是对称的 $\Leftrightarrow$ $s(R)=R$。
$R$是传递的 $\Leftrightarrow$ $t(R)=R$。

(2) $R_1,R_2$是非空集合$A$上的关系，且$R_1 \subseteq R_2,$则

$r(R_1) \subseteq r_(R_2)$。
$s(R_1) \subseteq s_(R_2)$。
$t(R_1) \subseteq t_(R_2)$。

(3) $R$是非空集合$A$上的关系，则

若$R$是自反的，则$s(R),t(R)$也是自反的。
若$R$是对称的，则$r(R),t(R)$也是对称的。
若$R$是传递的，则$r(R)$也是传递的。
即:对称闭包可能失去传递性。
因此，我们用$tsr(R)$表示$R$的自反、对称、传递闭包，有$tsr(R)=t(s(r(R)))$。
证明传递相关性质常用归纳法。

2.6 等价关系与划分

等价关系的定义

自反
传递
对称
若$\langle x,y \rangle \in R$，则称$x$等价于$y$，即$x \sim y$。

等价类的定义

关系图中每个联通块中的所有顶点构成一个等价类。
$R$是非空集合$A$上的等价关系，$x \in A$，则$x$的等价类(记作$[x]$或$[x]_R$)定义为$[x]_R = \{y | y \in A, \langle x,y \rangle \in R\}$。

等价类的性质

若$R$是非空集合$A$上的等价关系，则

$\forall x \in A, [x]$是$A$的非空子集。
$\forall x,y \in A,$如果$xRy$，则$[x] = [y]$。
$\forall x,y \in A,$如果$x \not \mathrel{R} y$,则$[x] \cap [y] = \emptyset$。
$\cup \{[x]|x \in A\}=A$。

商集的概念

以$R$的所有等价类作为元素的集合称为$A$关于$R$的商集，记作$A / R$,即$ A / R ={[x] | x \in A}$。

划分的定义

alt text

划分与等价关系

划分与等价关系是一一对应的。
因此，在求等价关系的时候应先写出划分。
注意:不要忘记$ \cup I_A$。

2.7 偏序关系

偏序关系的相关概念

自反
反对称
传递
若$\langle x,y \rangle \in \preceq$，则记作$x \preceq y$，读作小于或等于。
若$x \preceq y$且$x \not = y,$则称$x \prec y$，读作小于。
若$x \preceq y$或$y \preceq x$，则称$x$和$y$是可比的。
若$\forall x,y \in A,x$与$y$均可比，则称$R$是$A$上的全序关系(线序关系)。
$A$与$A$上的偏序关系$\preceq$共称为偏序集，记作$\langle A,\preceq \rangle$。
注意:写偏序集的时候也要考虑$I_A$(如果是$\prec$则不考虑)。
若$\langle A,\preceq \rangle$为偏序集，$\forall x,y \in A,$若$x \prec y$且不存在$z,x \prec z \prec y,$则称$y$覆盖$x$。

哈斯图的画法

先排列元素顺序。
若$x \prec y,$则把$x$画在$y$下方。
若$y$覆盖$x,$则连接$x$与$y$。

极小元、极大元、上界、下界、上确界、下确界的定义

(1)
设$\langle A,\preceq \rangle$为偏序集，$B \subseteq A,y \in B$
alt text

(2)
设$\langle A,\preceq \rangle$为偏序集，$B \subseteq A,y \in A$
alt text

关于这些概念的阐述

最小元一定要求其它元素与它可比，而极小元没有要求，只需要没有比它小的元素。在有穷集中，最小元不一定存在，存在即唯一；而极小元一定存在且可能有多个。极大元与最大元同此定义。
哈斯图中的孤立顶点既是极小元又是极大元。
$B$的最小元一定是$B$的下界，同时也是下确界。同样地，最大元一定是$B$的上界，同时也是上确界。但是下界(上界)不一定是最小元(最大元)，因为不一定是$B$中元素。
上界、下界、上确界、下确界都可能不存在，上确界(下确界)存在即唯一。
最大元一定是极大元，最小元一定是极小元。

调度问题的定义

alt text

调度问题的解决

若只有一台机器，且截止时间没有限制,则可以用拓扑排序解决问题。
拓扑排序:将偏序集扩张为对应全序集(不可比的元素随机可比)，忽略自反性，因此可能有多个结果。
用图论来说，有向边的起点一定比终点出现早，同时我们在图论中一般规定字典序最小，也是这个原因。

一些例题

例2.1.3
设$A,B,C,D$为任意集合，判断下列陈述是否正确，并说明理由。
(1) 若$A \times B = A \times C,$则 $B = C$.
思路：这种题一定先考虑空集，当$A = \emptyset$时举出反例。

(2) $A - (B \times C) = (A - B) \times (A - C)$
思路:还是考虑空集，当$A=B=C$时举出反例。

例2.3.5
设$A=\{a,b,d,e,f\},R=\{\langle a,b \rangle,\langle b,a \rangle,\langle d,e \rangle,\langle e,f \rangle,\langle f,d \rangle \}.$求最小的自然数$m$和$n$，使得$m < n$且$R^{m} = R^{n}$
思路:这种题目就是进行划分然后找$LCM$，得出$m=0.n=6$

一些容易错的题目

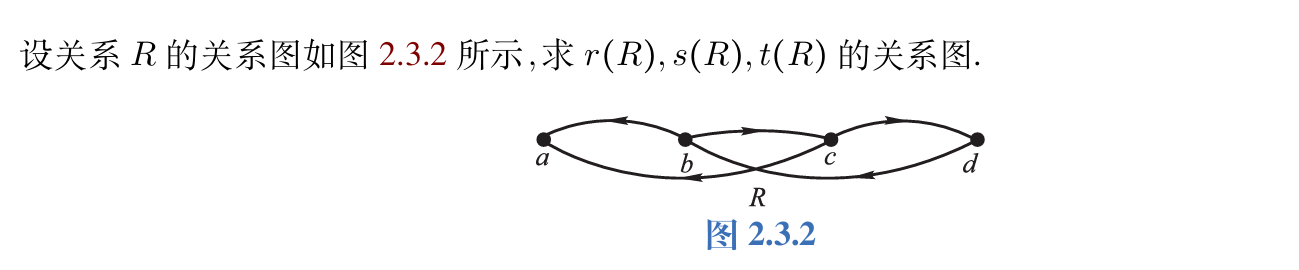
1. alt text

2.设$R_1,R_2$是$A$上的关系，求证:

\[t(R_1) \cup t(R_2) \subseteq t(R_1 \cup R_2) \]

思路:运用以下结论:$R_1 \subseteq R_2 \Rightarrow t(R_1) \subseteq t(R_2)$
解:$R_1 \subseteq R_1 \cup R_2,R_2 \subseteq R_1 \cup R_2$
于是有$t(R_1) \subseteq t(R_1 \cup R_2), t(R_2) \subseteq t(R_1 \cup R_2)$
于是有$t(R_1) \cup t(R_2) \subseteq t(R_1 \cup R_2)$

3.设$R_1$和$R_2$都是传递的，试举出反例证明$R_1 \circ R_2$不是传递的
解:考虑$A=\{1,2,3\},R_1=\{\langle 1,1 \rangle , \langle 2,3 \rangle \},R_2=\{\langle 1,2 \rangle, \langle 3,3 \rangle \},R_1 \circ R_2 = \{\langle 2,3 \rangle, \langle 1,2 \rangle \}$

4.设$R$是集合$A$上的等价关系，$|A|=n,|R|=r,|A / R|=m,$求证:$mr \geq n^2$
思路:运用一些课本知识
解:设$A / R =\{A_1,A_2,\ldots A_m\},|A_i|=n_i$
下证:$$ \cup (A_i \times A_i) = R $$

\[\begin{align*} & \forall \langle x,y \rangle \in \cup (A_i \times A_i)\\ \Leftrightarrow & \langle x,y \rangle \in A_i \times A_i \\ \Leftrightarrow & x,y \in A_i \\ \Leftrightarrow & \cup (A_i \times A_i) = R \\ \end{align*}\]

(因为对于一个商集(划分),$R$就是一个等价关系，有以下定义)
alt text
然后$r=\sum\limits_{i=1}^{m}n_i^2$,又$n=\sum\limits_{i=1}^{m}n_i$
因此由均值不等式(ACGN)得到$r=\sum\limits_{i=1}^{m}n_i^2 \geq \frac{(\sum\limits_{i=1}^{m}n_i)^2}{m}=\frac{n^2}{m},$即$mr \geq n^2$

5.对于任意集合$A,B,C,$若$A \times B \subseteq A \times C,$是否一定有$B \subseteq C$成立？
思路:这种题要额外考虑空集，若$A = \emptyset,$则不成立

6.设$A=\{\langle \emptyset,\{\emptyset,\{\emptyset \}\} \rangle,\langle \{\emptyset \}, \emptyset \rangle \},$求$A[\emptyset ],A \upharpoonright \emptyset$
思路:这题其实是在考概念，限制和像都是以一个集合作为运算对象，实际考虑其中元素的情况。而空集得到的自然是空集.

7.$R_1=\{\langle a,a \rangle, \langle a,b \rangle, \langle b,d \rangle \},$求$R_1^2$
思路:一个提醒:这种题一定要注意自反的元素，最后得到的元素一个也不能少

8.如果$R_1,R_2$具有传递性,$R_1 \circ R_2$是否还具有传递性？
思路:通过已有知识知道不一定具有传递性，我们只需找出反例.
解:令$R_1=\{\langle 1,2 \rangle,\langle 3,5 \rangle \},R_2=\{\langle 2,3 \rangle, \langle 5,4 \rangle \},$则$R_1 \circ R_2=\{\langle 1,3 \rangle, \langle 3,4 \rangle \},$可知$R_1 \circ R_2$不具有传递性

9.设$R_1,R_2$是非空集合$A$上的关系，且$R_1 \subseteq R_2$，求证:$t(R_1) \subseteq t(R_2)$
思路:证明传递性的题目通常使用归纳法
解:由已知知识，有$t(R_1)=R_1 \cup R_1^2 \cup R_1^3 \ldots,t(R_2)=R_2 \cup R_2^2 \cup R_2^3 \ldots$
我们先证明$\forall n \in N,R_1^n \subseteq R_2^n$
$n=1$时是显然的
假设$n$时满足$R_1^n \subseteq R_2^n$,$\forall \langle x,y \rangle \in R_1^{n+1},$存在$\langle x,z \rangle \in R_1^n,\langle z,y \rangle \in R_1,$,于是$\langle x,z \rangle \in R_2^n,\langle z,y \rangle \in R_2,$即$\langle x,y \rangle \in R_2^{n+1}$，因此有$R_1^{n+1} \subseteq R_2^{n+1}$
结论得证.
因此有$t(R_1) \subseteq t(R_2)$

10.$R$是非空集合$A$上的关系.
(1) 若$R$是自反的，则$s(R)$与$t(R)$也是自反的.
解:由于$R$是自反的，因此有$I_A \subseteq R,$又由于$s(R)=R \cup R^{-1},t(R)=R \cup R^2 \cup R^3 \ldots,$因此有$I_A \subseteq s(R),I_A \subseteq t(R),$即$s(R)$与$t(R)$也是自反的.

(2) 若$R$是传递的，则$r(R)$也是传递的.
解:由于$R$是传递的，因此有$R \circ R \subseteq R$,而

\[\begin{align*} & r(R) \circ r(R) \\ = & (R \cup I_A) \circ (R \cup I_A) \\ = & (R \circ R) \cup (R \circ I_A) \cup (R \circ I_A) \cup (I_A \circ I_A) \\ = & (R \circ R) \cup (R \circ I_A) \cup I_A \\ = & (R \circ R) \cup R \cup I_A \\ \subseteq & R \cup I_A = r(R) \\ \end{align*}\]

证毕.

11.对于给定的$A$和$R$，判断$R$是否为$A$上的等价关系.
$A=P(S),C \subseteq S,\forall X,Y \in A, XRY \Leftrightarrow X \oplus Y \subseteq C$
证明:自反性和对称性是显然的
下面证明传递性,$\forall X,Y,Z \in A,$有$X \oplus Y \subseteq C,Y \oplus Z \subseteq C$
由于

\[\begin{align*} & X \oplus Z \\ = & X \oplus Y \oplus Y \oplus Z \\ = & (X \oplus Y) \oplus (Y \oplus Z) \\ \subseteq & C \\ \end{align*}\]

传递性证毕.

12.对任意非空的集合$A,A$的非空子集族$P(A) - \{\emptyset \}$是否构成$A$的划分?
思路:这题要分类讨论
解:若$|A|=1$，则构成划分；反之则不构成

13.设$R$为$A$上的自反和传递关系，证明$R \cap R^{-1}$是$A$上的等价关系
证明:由于$R$有自反性，因此$I_A \subseteq R, \Rightarrow I_A \subseteq R^{-1},I_A \subseteq R \cap R^{-1} ,$即$R \cap R^{-1}$有自反性.
对称性:$\forall \langle x,y \rangle \in R \cap R^{-1},$由于$\langle x,y \rangle \in R, \Rightarrow \langle y,x \rangle \in R^{-1}$,由于$\langle x,y \in R^{-1}, \Rightarrow \langle y,x \rangle \in R,$,因此$\langle x,y \rangle \in R \cap R^{-1}$，即$R \cap \R^{-1}$有对称性.
传递性:

\[\begin{align*} & \forall \langle x,z \rangle,\langle z,y \rangle \in R \cap R^{-1} \\ \Rightarrow & \langle x,z \rangle \in R \wedge \langle z,y \rangle \in R \wedge \langle x,z \rangle \in R^{-1} \wedge \langle z,y \rangle \in R^{-1} \\ \Rightarrow & \langle x,z \rangle \in R \wedge \langle z,y \rangle \in R \wedge \langle z,x \rangle \in R \wedge \langle y,z \rangle \in R \\ \Rightarrow & \langle x,y \rangle \in R \wedge \langle y,x \rangle \in R \\ \Rightarrow & \langle x,y \rangle \in R \cap R^{-1} \\ \end{align*}\]

传递性证毕.

14.设$R$是$A$上的自反关系，证明:$R$是$A$上等价关系的充要条件是:若$\langle a,b \rangle \in R$且$\langle a,c \rangle \in R,$则有$\langle b,c \rangle \in R$
证明:必要性是显然的.
下面证明充分性.
对称性:$\forall \langle a,b \rangle \in R, \langle a,c \rangle \in R, \Rightarrow \langle b,c \rangle \in R$
$\Leftrightarrow \forall \langle a,c \rangle \in R, \langle a,b \rangle \in R, \langle c,b \rangle \in R$
对称性证毕.
传递性:$\forall \langle x,y \rangle \in R,\langle y,z \rangle \in R, \Rightarrow \langle x,z \rangle \in R$
$\Leftrightarrow \langle y,x \rangle \in R,\langle y,z \rangle \in R, \langle x,z \rangle \in R$
传递性证毕.

15.指出下面命题证明时的错误.
命题:设$R$是集合$A$上的对称、传递关系，则$R$是自反的.
证明:设$x \in A$,根据对称性由$\langle x,y \rangle \in R$得到$\langle y,x \rangle \in R,$再使用传递性得到$\langle x,x \rangle \in R.$从而证明了$R$的自反性.
思路:$I_A$中的所有元素不一定都在$R$中.

下学期，也请各位继续关注：
《System beats!》
《大二病也要学离散！》
《数算の旅》
《某信息学的概率统计》
还有——

《我的算法竞赛不可能这么可爱》

本期到此结束！

alt text

posted @ 2025-08-09 09:38 elainafan 阅读(12) 评论(0) 收藏举报

刷新页面返回顶部

elainafan

【大二病也要学离散！】第二章 二元关系

2.1 有序对与笛卡尔积

有序对的概念

笛卡尔积的概念

笛卡尔积的性质

2.2 二元关系

二元关系的定义与性质

特殊的二元关系

表示二元关系的常见方法

2.3 关系的运算

相关概念

二元关系的运算规律

\(R\)的次幂的定义

\(R\)次幂的性质

2.4 关系的性质

关系的性质

性质成立的充要条件

集合运算与性质的关系

性质在不同表示法下的性质

集合运算的相关性质

2.5 关系的闭包

闭包的三个条件

闭包的计算

关系矩阵与关系图求闭包:

计算机求传递闭包

闭包的主要性质:

2.6 等价关系与划分

等价关系的定义

等价类的定义

等价类的性质

商集的概念

划分的定义

划分与等价关系

2.7 偏序关系

偏序关系的相关概念

哈斯图的画法

极小元、极大元、上界、下界、上确界、下确界的定义

关于这些概念的阐述

调度问题的定义

调度问题的解决

一些例题

一些容易错的题目

《我的算法竞赛不可能这么可爱》

公告

【大二病也要学离散！】第二章二元关系