【leetcode刷题】动态规划 Part 2 网格图DP

好几天没写博客了

今天来总结一下灵神题单的第二部分：网格图DP
怎么说呢，还是有点难度的，而且很全面
对于DP基础的巩固大有裨益
下面看题:

1824:最少侧跳次数

给你一个长度为 n + 1 的数组 obstacles ，其中 obstacles[i] （取值范围从 0 到 3）表示在点 i 处的 obstacles[i] 跑道上有一个障碍。如果 obstacles[i] == 0 ，那么点 i 处没有障碍。任何一个点的三条跑道中 最多有一个 障碍。

• 比方说，如果 obstacles[2] == 1 ，那么说明在点 2 处跑道 1 有障碍。

这只青蛙从点 i 跳到点 i + 1 且跑道不变的前提是点 i + 1 的同一跑道上没有障碍。为了躲避障碍，这只青蛙也可以在 同一个 点处 侧跳 到 另外一条 跑道（这两条跑道可以不相邻），但前提是跳过去的跑道该点处没有障碍。

• 比方说，这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。

这只青蛙从点 0 处跑道 2 出发，并想到达点 n 处的 任一跑道 ，请你返回 最少侧跳次数 。

注意：点 0 处和点 n 处的任一跑道都不会有障碍。

示例 1：

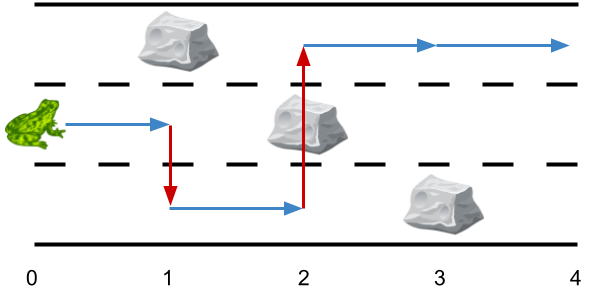
输入：obstacles = [0,1,2,3,0]
输出：2
解释：最优方案如上图箭头所示。总共有 2 次侧跳（红色箭头）。
注意，这只青蛙只有当侧跳时才可以跳过障碍（如上图点 2 处所示）。

示例 2：

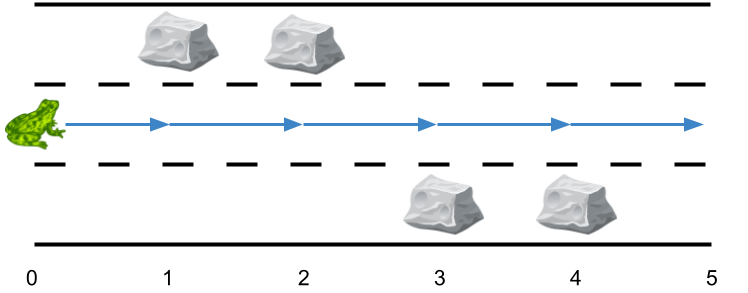
输入：obstacles = [0,1,1,3,3,0]
输出：0
解释：跑道 2 没有任何障碍，所以不需要任何侧跳。

示例 3：

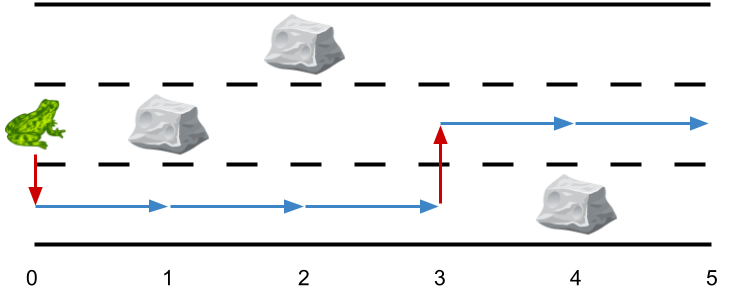
输入：obstacles = [0,2,1,0,3,0]
输出：2
解释：最优方案如上图所示。总共有 2 次侧跳。

提示：

• obstacles.length == n + 1
• 1 <= n <= 5 * 105
• 0 <= obstacles[i] <= 3
• obstacles[0] == obstacles[n] == 0

Solution

想了一会，不是什么难题
把三个状态设出来，然后直接转移就可以

class Solution {
public:
    int minSideJumps(vector<int>& obstacles) {
        int n=obstacles.size();
        n--;
        const int INF=1e9;
        vector<vector<int>>dp(n+5,vector<int>(4,INF));
        dp[0][2]=0;dp[0][1]=dp[0][3]=1;
        for(int i=1;i<=n;i++){
            if(obstacles[i]==0){
                dp[i][1]=min(dp[i][1],min(dp[i-1][1],min(dp[i-1][2]+1,dp[i-1][3]+1)));
                dp[i][2]=min(dp[i][2],min(dp[i-1][2],min(dp[i-1][1]+1,dp[i-1][3]+1)));
                dp[i][3]=min(dp[i][3],min(dp[i-1][3],min(dp[i-1][1]+1,dp[i-1][2]+1)));
            }
            else{
                if(obstacles[i]==1){
                    dp[i][2]=min(dp[i][2],min(dp[i-1][3]+1,dp[i-1][2]));
                    dp[i][3]=min(dp[i][3],min(dp[i-1][2]+1,dp[i-1][3]));
                }
                else if(obstacles[i]==2){
                    dp[i][1]=min(dp[i][1],min(dp[i-1][1],dp[i-1][3]+1));
                    dp[i][3]=min(dp[i][3],min(dp[i-1][1]+1,dp[i-1][3]));
                }
                else{
                    dp[i][1]=min(dp[i][1],min(dp[i-1][1],dp[i-1][2]+1));
                    dp[i][2]=min(dp[i][2],min(dp[i-1][1]+1,dp[i-1][2]));
                }
            }
        }
        return min(dp[n][1],min(dp[n][2],dp[n][3]));
    }
};

174：地下城游戏

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只 向右 或 向下 移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

注意：任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

示例 1：

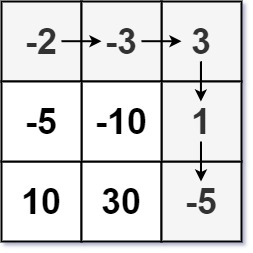
输入：dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出：7
解释：如果骑士遵循最佳路径：右 -> 右 -> 下 -> 下 ，则骑士的初始健康点数至少为 7 。

示例 2：

输入：dungeon = [[0]]
输出：1

提示：

• m == dungeon.length
• n == dungeon[i].length
• 1 <= m, n <= 200
• -1000 <= dungeon[i][j] <= 1000

Solution

这道题就是我之前讲的刷表法
什么是刷表法，与之相对的填表法又是什么？
我们可以看到，填表法，就是对于一个状态，永远用已知状态来更新
而刷表法就是，对于用已知状态多次更新未来的状态
可能会觉得，这有什么差别，其实差别在于它的主动性
比如这道题，如果从起点更新到终点，因为无法预知这一点的最大被扣血量跟当前血量两者的高低究竟对最终答案有何帮助，我们得从终点开始往起点刷表。
已知终点的最小可生存血量，然后按照如下文代码所示的转移方程来做
（其实这种题本来应该是二分+搜索，不知道为啥跑到DP来）

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int m=dungeon.size();
        int n=dungeon[0].size();
        vector<vector<int>>dp(m+5,vector<int>(n+5,0));
        if(dungeon[m-1][n-1]>0) dp[m-1][n-1]=0;
        else dp[m-1][n-1]=dungeon[m-1][n-1];
        for(int i=m-1;i>=0;i--){
            for(int j=n-1;j>=0;j--){
                if(i==m-1&&j==n-1) continue;
                int ax=i+1,ay=j;
                int bx=i,by=j+1;
                if(ax>=m||ay>=n){
                    dp[i][j]=min(dp[bx][by]+dungeon[i][j],0);
                }
                else if(bx>=m||by>=n){
                    dp[i][j]=min(dp[ax][ay]+dungeon[i][j],0);
                }
                else{
                    dp[i][j]=min(max(dp[ax][ay],dp[bx][by])+dungeon[i][j],0);
                }
            }
        }
        return dp[0][0]>=0?1:-dp[0][0]+1;
    }
};

329:矩阵中的最长递增路径

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

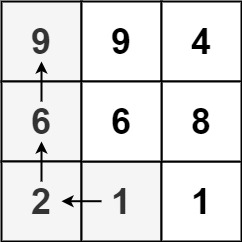
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

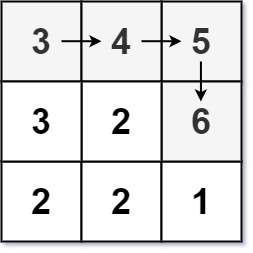
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= \(2^{31}\) - 1

Solution

滑雪老题，不解释

class Solution {
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
       int m=matrix.size();
        int n=matrix[0].size();
        vector<vector<int>>dp(m+5,vector<int>(n+5,1));
        struct node{
            int x,y;
            int num;
            bool operator<(const node &other){
                return num<other.num;
            }
        }ma[m*n+5];
        int cnt=0;
        int dx[5]={0,1,-1,0,0},dy[5]={0,0,0,1,-1};
        for(int i=0;i<=m-1;i++){
            for(int j=0;j<=n-1;j++){
                ma[++cnt].x=i;ma[cnt].y=j;ma[cnt].num=matrix[i][j];
            }
        }
        sort(ma+1,ma+1+m*n);
        for(int i=1;i<=m*n;i++){
            int x=ma[i].x,y=ma[i].y;
            for(int j=1;j<=4;j++){
                int ax=x+dx[j],ay=y+dy[j];
                if(ax<0||ay<0||ax>=m||ay>=n) continue;
                if(matrix[ax][ay]>ma[i].num) dp[ax][ay]=max(dp[ax][ay],dp[x][y]+1);  
            }
        }
        int res=0;
        for(int i=0;i<=m-1;i++){
            for(int j=0;j<=n-1;j++){
                res=max(res,dp[i][j]);
            }
        }
        return res;
    }
};

2267：检查是否有合法括号字符串路径

一个括号字符串是一个 非空 且只包含 '(' 和 ')' 的字符串。如果下面 任意 条件为 真 ，那么这个括号字符串就是 合法的 。

• 字符串是 () 。
• 字符串可以表示为 AB（A 连接 B），A 和 B 都是合法括号序列。
• 字符串可以表示为 (A) ，其中 A 是合法括号序列。

给你一个 m x n 的括号网格图矩阵 grid 。网格图中一个 合法括号路径 是满足以下所有条件的一条路径：

• 路径开始于左上角格子 (0, 0) 。
• 路径结束于右下角格子 (m - 1, n - 1) 。
• 路径每次只会向 下 或者向 右 移动。
• 路径经过的格子组成的括号字符串是 合法 的。

如果网格图中存在一条 合法括号路径 ，请返回 true ，否则返回 false 。

示例 1：

输入：grid = [ ["(","(","("],[")","(",")"],["(","(",")"],["(","(",")"] ]
输出：true
解释：上图展示了两条路径，它们都是合法括号字符串路径。
第一条路径得到的合法字符串是 "()(())" 。
第二条路径得到的合法字符串是 "((()))" 。
注意可能有其他的合法括号字符串路径。

示例 2：

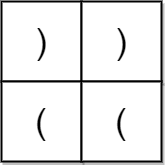
输入：grid = [ [")",")"],["(","("] ]
输出：false
解释：两条可行路径分别得到 "))(" 和 ")((" 。由于它们都不是合法括号字符串，我们返回 false 。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• grid[i][j] 要么是 '(' ，要么是 ')' 。

Solution

我们可以将左括号看成1，右括号看成-1，这样只需要找是否有一条能到达终点（并且到的值为0），同时在路径任意一点值都不为负数的路径。
直接设成三维DP,第三维表示当前的值就可以

class Solution {
public:
    bool hasValidPath(vector<vector<char>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        if((m+n)%2==0) return false;
        vector<vector<int>>ma(m+5,vector<int>(n+5,0));
        for(int i=0;i<=m-1;i++){
            for(int j=0;j<=n-1;j++){
                if(grid[i][j]=='(') ma[i][j]=1;
                else ma[i][j]=-1;
            }
        }
        vector<vector<vector<bool>>>dp(m+5,vector<vector<bool>>(n+5,vector<bool>(205,false)));
        if(ma[0][0]==1) dp[0][0][1]=true;
        for(int i=0;i<=m-1;i++){
            for(int j=0;j<=n-1;j++){
                if(i==0&&j==0) continue;
                int ax=i-1,ay=j;
                int bx=i,by=j-1;
                for(int k=0;k<=m+n;k++){
                    if(k+ma[i][j]<0||k+ma[i][j]>m+n) continue;
                    if(ax>=0&&ay>=0) dp[i][j][k+ma[i][j]]=dp[i][j][k+ma[i][j]]|dp[ax][ay][k];
                    if(bx>=0&&by>=0) dp[i][j][k+ma[i][j]]=dp[i][j][k+ma[i][j]]|dp[bx][by][k]; 
                }
            }
        }
        return dp[m-1][n-1][0];
    }
};

1937：扣分后的最大得分

你的得分方式为：每一行 中选取一个格子，选中坐标为 (r, c) 的格子会给你的总得分 增加 points[r][c] 。

然而，相邻行之间被选中的格子如果隔得太远，你会失去一些得分。对于相邻行 r 和 r + 1 （其中 0 <= r < m - 1），选中坐标为 (r, c1) 和 (r + 1, c2) 的格子，你的总得分 减少 abs(c1 - c2) 。

请你返回你能得到的 最大 得分。

abs(x) 定义为：

• 如果 x >= 0 ，那么值为 x 。
• 如果 x < 0 ，那么值为 -x 。

示例 1：

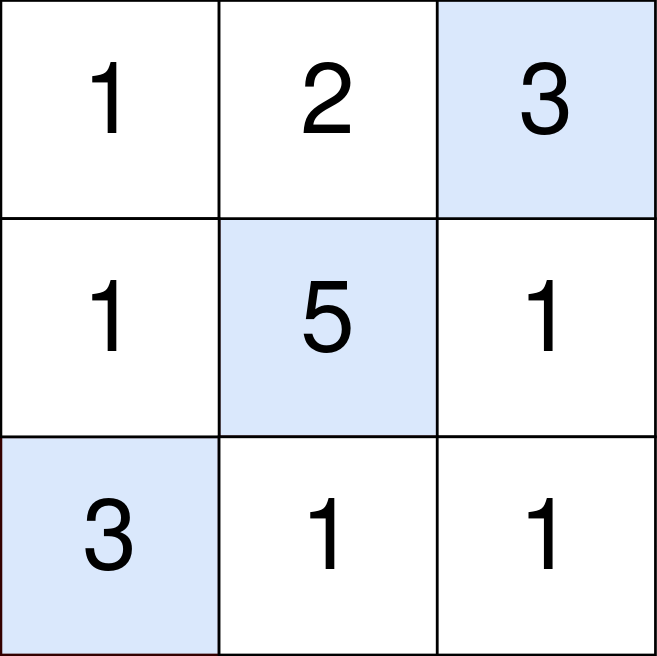
输入：points = [ [1,2,3],[1,5,1],[3,1,1] ]
输出：9
解释：
蓝色格子是最优方案选中的格子，坐标分别为 (0, 2)，(1, 1) 和 (2, 0) 。
你的总得分增加 3 + 5 + 3 = 11 。
但是你的总得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。
你的最终得分为 11 - 2 = 9 。

示例 2：

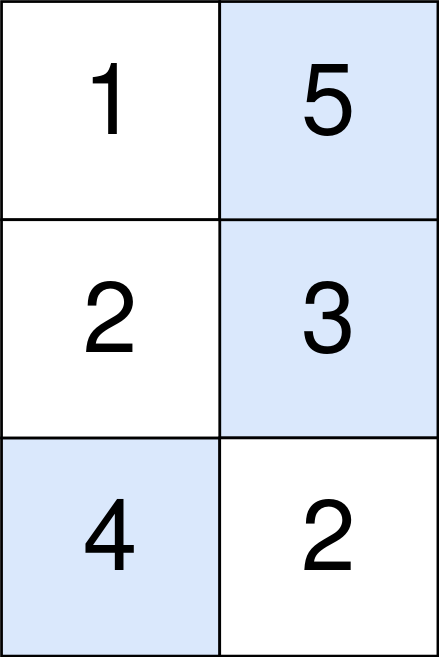
输入：points = [ [1,5],[2,3],[4,2] ]
输出：11
解释：
蓝色格子是最优方案选中的格子，坐标分别为 (0, 1)，(1, 1) 和 (2, 0) 。
你的总得分增加 5 + 3 + 4 = 12 。
但是你的总得分需要扣除 abs(1 - 1) + abs(1 - 0) = 1 。
你的最终得分为 12 - 1 = 11 。

提示：

• m == points.length
• n == points[r].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 0 <= points[r][c] <= 105

Solition

如果直接更新，这道题会因时间复杂度过大而超时
我们需要优化
目前看来，动态规划的优化，前缀和绝对是一个需要考虑的方面
我们写出转移方程

\[dp[i][j]=points[i][j]+max(dp[i-1][k])-|k-j| \]

好了，这个绝对值能不能拆呢？
我们把上式化简为

\[f[i][j] = \begin{cases} \text{points}[i][j] - j + \max\limits_{k \leq j} \left( f[i-1][k] + k \right), & k \leq j \\ \text{points}[i][j] + j + \max\limits_{k > j} \left( f[i-1][k] - k \right), & k > j \end{cases} \]

于是，在每层转移之前，先正序倒序前缀处理出最大值，就能达成目的了，降了一维时间。

class Solution {
public:
    long long maxPoints(vector<vector<int>>& points) {
        int m=points.size();
        int n=points[0].size();
        const int INF=1e9;
        vector<vector<long long>>dp(m+5,vector<long long>(n+5,-INF));
        for(int i=0;i<=n-1;i++){
            dp[0][i]=points[0][i];
        }
        vector<vector<long long>>ma_1(m+5,vector<long long>(n+5,-INF));
        vector<vector<long long>>ma_2(m+5,vector<long long>(n+5,-INF));
        for(int i=1;i<=m-1;i++){
            ma_1[i-1][0]=dp[i-1][0];
            for(int j=1;j<=n-1;j++){
                ma_1[i-1][j]=max(ma_1[i-1][j-1],dp[i-1][j]+j);
            }
            ma_2[i-1][n-1]=dp[i-1][n-1]-(n-1);
            for(int j=n-2;j>=0;j--){
                ma_2[i-1][j]=max(ma_2[i-1][j+1],dp[i-1][j]-j);
            }
            for(int j=0;j<=n-1;j++){
                dp[i][j]=max(dp[i][j],max(ma_1[i-1][j]-j,ma_2[i-1][j]+j)+points[i][j]);
            }
        }
        long long res=-INF;
        for(int i=0;i<=n-1;i++) res=max(res,dp[m-1][i]);
        return res;
    }
};

3363：最多可收集的水果数目

给你一个大小为 n x n 的二维整数数组 fruits ，其中 fruits[i][j] 表示房间 (i, j) 中的水果数目。有三个小朋友 一开始 分别从角落房间 (0, 0) ，(0, n - 1) 和 (n - 1, 0) 出发。

每一位小朋友都会 恰好 移动 n - 1 次，并到达房间 (n - 1, n - 1) ：

• 从 (0, 0) 出发的小朋友每次移动从房间 (i, j) 出发，可以到达 (i + 1, j + 1) ，(i + 1, j) 和 (i, j + 1) 房间之一（如果存在）。
• 从 (0, n - 1) 出发的小朋友每次移动从房间 (i, j) 出发，可以到达房间 (i + 1, j - 1) ，(i + 1, j) 和 (i + 1, j + 1) 房间之一（如果存在）。
• 从 (n - 1, 0) 出发的小朋友每次移动从房间 (i, j) 出发，可以到达房间 (i - 1, j + 1) ，(i, j + 1) 和 (i + 1, j + 1) 房间之一（如果存在）。

当一个小朋友到达一个房间时，会把这个房间里所有的水果都收集起来。如果有两个或者更多小朋友进入同一个房间，只有一个小朋友能收集这个房间的水果。当小朋友离开一个房间时，这个房间里不会再有水果。

请你返回三个小朋友总共 最多 可以收集多少个水果。

示例 1：

输入：fruits = [ [1,2,3,4],[5,6,8,7],[9,10,11,12],[13,14,15,16] ]

输出：100

解释：

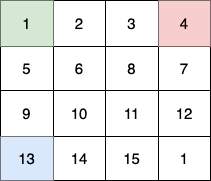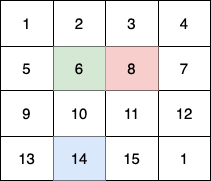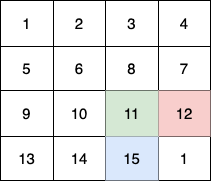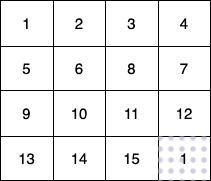
这个例子中：

• 第 1 个小朋友（绿色）的移动路径为 (0,0) -> (1,1) -> (2,2) -> (3, 3) 。
• 第 2 个小朋友（红色）的移动路径为 (0,3) -> (1,2) -> (2,3) -> (3, 3) 。
• 第 3 个小朋友（蓝色）的移动路径为 (3,0) -> (3,1) -> (3,2) -> (3, 3) 。

他们总共能收集 1 + 6 + 11 + 1 + 4 + 8 + 12 + 13 + 14 + 15 = 100 个水果。

示例 2：

输入：fruits = [ [1,1],[1,1] ]

输出：4

解释：

这个例子中：

• 第 1 个小朋友移动路径为 (0,0) -> (1,1) 。
• 第 2 个小朋友移动路径为 (0,1) -> (1,1) 。
• 第 3 个小朋友移动路径为 (1,0) -> (1,1) 。

他们总共能收集 1 + 1 + 1 + 1 = 4 个水果。

提示：

• 2 <= n == fruits.length == fruits[i].length <= 1000
• 0 <= fruits[i][j] <= 1000

Solution

丁真题
第一个点：第一个小朋友永远走对角线，很容易看出来
第二个点：第二和第三个小朋友的路线是互不干涉的，所以直接同时处理就可以了

class Solution {
public:
    int maxCollectedFruits(vector<vector<int>>& fruits) {
        int ans=0;
        int n=fruits.size();
        for(int i=0;i<=n-1;i++){
            ans+=fruits[i][i];
            fruits[i][i]=0;
        }
        vector<vector<int>>dp(n+5,vector<int>(n+5,0));
        vector<vector<int>>fdp(n+5,vector<int>(n+5,0));
        dp[n-1][0]=fruits[n-1][0];fdp[0][n-1]=fruits[0][n-1];
        for(int i=1;i<=n-1;i++){
            for(int j=n/2;j<=n-1;j++){
                if(j<n-1-i) continue;
                int ax=j-1,bx=j,cx=j+1;
                if(ax>=n-i){
                    dp[j][i]=max(dp[j][i],dp[ax][i-1]+fruits[j][i]);
                }
                if(bx>=n-i){
                    dp[j][i]=max(dp[j][i],dp[bx][i-1]+fruits[j][i]);
                }
                if(cx>=n-i){
                    dp[j][i]=max(dp[j][i],dp[cx][i-1]+fruits[j][i]);
                }
            }
        }
        for(int i=1;i<=n-1;i++){
            for(int j=n/2;j<=n-1;j++){
                if(j<n-1-i) continue;
                int ax=j-1,bx=j,cx=j+1;
                if(ax>=n-i){
                    fdp[i][j]=max(fdp[i][j],fdp[i-1][ax]+fruits[i][j]);
                }
                if(bx>=n-i){
                    fdp[i][j]=max(fdp[i][j],fdp[i-1][bx]+fruits[i][j]);
                }
                if(cx>=n-i){
                    fdp[i][j]=max(fdp[i][j],fdp[i-1][cx]+fruits[i][j]);
                }
            }
        }
        return dp[n-1][n-1]+fdp[n-1][n-1]+ans;
    }
};

1463：摘樱桃

你有两个机器人帮你收集樱桃，机器人 1 从左上角格子 (0,0) 出发，机器人 2 从右上角格子 (0, cols-1) 出发。

请你按照如下规则，返回两个机器人能收集的最多樱桃数目：

• 从格子 (i,j) 出发，机器人可以移动到格子 (i+1, j-1)，(i+1, j) 或者 (i+1, j+1) 。
• 当一个机器人经过某个格子时，它会把该格子内所有的樱桃都摘走，然后这个位置会变成空格子，即没有樱桃的格子。
• 当两个机器人同时到达同一个格子时，它们中只有一个可以摘到樱桃。
• 两个机器人在任意时刻都不能移动到 grid 外面。
• 两个机器人最后都要到达 grid 最底下一行。

示例 1：

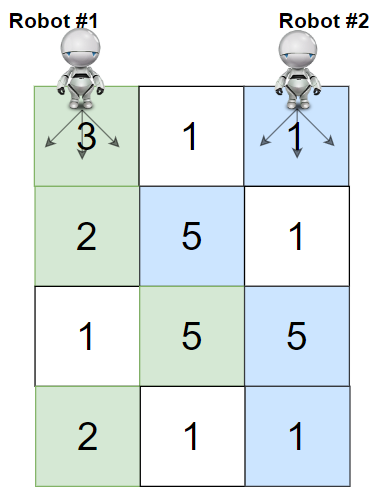
输入：grid = [ [3,1,1],[2,5,1],[1,5,5],[2,1,1] ]
输出：24
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12 。
机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12 。
樱桃总数为： 12 + 12 = 24 。

示例 2：

输入：grid = [ [1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6] ]
输出：28
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17 。
机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11 。
樱桃总数为： 17 + 11 = 28 。

示例 3：

输入：grid = [ [1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3] ]
输出：22

示例 4：

输入：grid = [ [1,1],[1,1] ]
输出：4

提示：

• rows == grid.length
• cols == grid[i].length
• 2 <= rows, cols <= 70
• 0 <= grid[i][j] <= 100

Solution

由于两个机器人是一直在同一行的，所以我们只需要一个三维数组
然后跟传纸条有点像，直接更新就行

class Solution {
public:
    int cherryPickup(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        const int INF=1e9+7;
        vector<vector<vector<int>>>dp(m+5,vector<vector<int>>(n+5,vector<int>(n+5,-INF)));
        int dx[10]={0,1,1,1,-1,-1,-1,0,0,0};
        int dy[10]={0,-1,0,1,-1,0,1,-1,0,1};
        dp[0][0][n-1]=grid[0][0]+grid[0][n-1];
        for(int i=1;i<=m-1;i++){
            for(int j=0;j<=n-1;j++){
                for(int k=0;k<=n-1;k++){
                    for(int v=1;v<=9;v++){
                        int ax=j+dx[v],ay=k+dy[v];
                        if(ax<0||ax>=n||ay<0||ay>=n) continue;
                        if(dp[i-1][ax][ay]<0) continue; 
                        if(j==k) dp[i][j][k]=max(dp[i][j][k],dp[i-1][ax][ay]+grid[i][j]);
                        else dp[i][j][k]=max(dp[i][j][k],dp[i-1][ax][ay]+grid[i][j]+grid[i][k]); 
                    }
                }
            }
        }
        int res=-INF;
        for(int i=0;i<=n-1;i++){
            for(int j=0;j<=n-1;j++){
                res=max(dp[m-1][i][j],res);
            }
        }
        return res;
    }
};

3453：最长V形线段的长度

V 形对角线段 定义如下：

• 线段从 1 开始。
• 后续元素按照以下无限序列的模式排列：2, 0, 2, 0, ...。
• 该线段：
  • 起始于某个对角方向（左上到右下、右下到左上、右上到左下或左下到右上）。
  • 沿着相同的对角方向继续，保持 序列模式 。
  • 在保持 序列模式 的前提下，最多允许 一次顺时针 90 度转向 另一个对角方向。

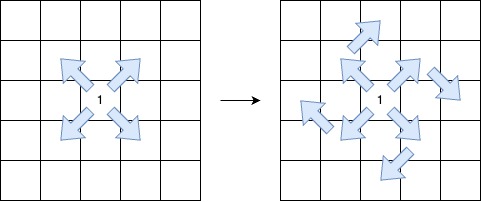
返回最长的 V 形对角线段 的 长度 。如果不存在有效的线段，则返回 0。

示例 1：

输入： grid = [ [2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2] ]

输出： 5

解释：

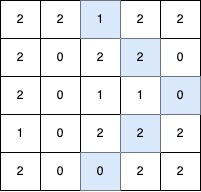
最长的 V 形对角线段长度为 5，路径如下：(0,2) → (1,3) → (2,4)，在 (2,4) 处进行 顺时针 90 度转向 ，继续路径为 (3,3) → (4,2)。

示例 2：

输入： grid = [ [2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2] ]

输出： 4

解释：

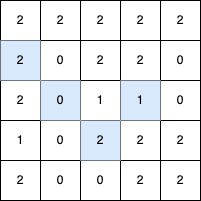
最长的 V 形对角线段长度为 4，路径如下：(2,3) → (3,2)，在 (3,2) 处进行 顺时针 90 度转向 ，继续路径为 (2,1) → (1,0)。

示例 3：

输入： grid = [ [1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0] ]

输出： 5

解释：

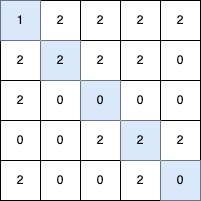
最长的 V 形对角线段长度为 5，路径如下：(0,0) → (1,1) → (2,2) → (3,3) → (4,4)。

示例 4：

输入： grid = [ [1] ]

输出： 1

解释：

最长的 V 形对角线段长度为 1，路径如下：(0,0)。

提示：

• n == grid.length
• m == grid[i].length
• 1 <= n, m <= 500
• grid[i][j] 的值为 0、1 或 2。

Solution

这道题其实不好做，我也是看题解才知道的
首先有四个方向，不妨定右上为0，一直到左上为3
先枚举每个0或者2在每个方向上的最长长度
注意顺序：如果1、2方向需要从上到下，反之从上到下
然后再找每个1 对这个1的四个方向的2 分别算出已经过的长度跟转向后可以走的长度之和，逐一取最大值

class Solution {
public:
    int lenOfVDiagonal(vector<vector<int>>& grid) {
        int n=grid.size();
        int m=grid[0].size();
        int dp[n+5][m+5][4];
        int ddx[4]={-1,1,1,-1},ddy[4]={1,1,-1,-1};
        for(int i=0;i<=n-1;i++){
            for(int j=0;j<=m-1;j++){
                if(grid[i][j]==1) continue;
                int ax=i+ddx[0],ay=j+ddy[0];
                int bx=i+ddx[3],by=j+ddy[3];
                if(ax<0||ay<0||ax>=n||ay>=m) dp[i][j][0]=1;
                else if(grid[i][j]+grid[ax][ay]!=2) dp[i][j][0]=1;
                else dp[i][j][0]=dp[ax][ay][0]+1;
                if(bx<0||by<0||bx>=n||by>=m) dp[i][j][3]=1;
                else if(grid[i][j]+grid[bx][by]!=2) dp[i][j][3]=1;
                else dp[i][j][3]=dp[bx][by][3]+1;
            }
        }
        for(int i=n-1;i>=0;i--){
            for(int j=m-1;j>=0;j--){
                if(grid[i][j]==1) continue;
                int cx=i+ddx[1],cy=j+ddy[1];
                int dx=i+ddx[2],dy=j+ddy[2];
                if(cx<0||cy<0||cx>=n||cy>=m) dp[i][j][1]=1;
                else if(grid[i][j]+grid[cx][cy]!=2) dp[i][j][1]=1; 
                else dp[i][j][1]=dp[cx][cy][1]+1;
                if(dx<0||dy<0||dx>=n||dy>=m) dp[i][j][2]=1;
                else if(grid[i][j]+grid[dx][dy]!=2) dp[i][j][2]=1;
                else dp[i][j][2]=dp[dx][dy][2]+1;
            }
        }
        int res=0;
        for(int i=0;i<=n-1;i++){
            for(int j=0;j<=m-1;j++){
                if(grid[i][j]!=1) continue;
                for(int k=0;k<=3;k++){
                    int ax=i+ddx[k],ay=j+ddy[k];
                    int l=1;
                    res=max(res,1);
                    int temp=2;
                    while(ax>=0&&ay>=0&&ax<=n-1&&ay<=m-1&&grid[ax][ay]==temp){
                        l+=1;
                        res=max(res,l+dp[ax][ay][(k+1)%4]-1);
                        ax+=ddx[k],ay+=ddy[k];
                        temp=2-temp;
                    }
                }
            }
        }
        return res;
    }
};

状态确实不好设计

怎么看个动漫还能复习法语的（笑）