【算法刷题】动态规划 Day4
还是接着刷DP
今天的题目有两题是自己想出来的,一题是想了很久看题解的
虽然想出来的都是黄题就是了
P2758 编辑距离
题目描述
设 \(A\) 和 \(B\) 是两个字符串。我们要用最少的字符操作次数,将字符串 \(A\) 转换为字符串 \(B\)。这里所说的字符操作共有三种:
- 删除一个字符;
- 插入一个字符;
- 将一个字符改为另一个字符。
\(A, B\) 均只包含小写字母。
输入格式
第一行为字符串 \(A\);第二行为字符串 \(B\);字符串 \(A, B\) 的长度均小于 \(2000\)。
输出格式
只有一个正整数,为最少字符操作次数。
输入输出样例 #1
输入 #1
sfdqxbw
gfdgw
输出 #1
4
说明/提示
对于 \(100 \%\) 的数据,\(1 \le |A|, |B| \le 2000\)。
解法&&个人感想
对于这种多序列的题目(至少洛谷官方是这么分类的),我们通常需要将\(dp\)数组化成至少二维的,通过两边的遍历来转移,不需要担心无后效性的问题(如果实在担心可以自己验证)
那么,我们就开始自己推了
对了,我们在没过的时候通常还需要考虑初始化条件(如果确定转移方程没有错的话),比如这道题我就是漏考虑了初始化情况,导致一开始只有89pts
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 2005
using namespace std;
int dp[maxn][maxn];
string a,b;
const int INF=1e9;
int main(){
cin>>a>>b;
int la=a.length(),lb=b.length();
for(int i=0;i<=la;i++){
for(int j=0;j<=lb;j++){
dp[i][j]=INF;
}
}
dp[0][0]=0;
for(int i=1;i<=la;i++) dp[i][0]=i;
for(int i=1;i<=lb;i++) dp[0][i]=i;
for(int i=1;i<=la;i++){
for(int j=1;j<=lb;j++){
if(a[i-1]==b[j-1]) dp[i][j]=min(dp[i][j],dp[i-1][j-1]);
else{
dp[i][j]=min(dp[i][j],dp[i-1][j-1]+1);
dp[i][j]=min(dp[i][j],dp[i][j-1]+1);
dp[i][j]=min(dp[i][j],dp[i-1][j]+1);
}
}
}
cout<<dp[la][lb]<<endl;
system("pause");
return 0;
}
P1435 [IOI 2000] 回文字串
题目背景
IOI2000 第一题
题目描述
回文词是一种对称的字符串。任意给定一个字符串,通过插入若干字符,都可以变成回文词。此题的任务是,求出将给定字符串变成回文词所需要插入的最少字符数。
比如 \(\verb!Ab3bd!\) 插入 \(2\) 个字符后可以变成回文词 \(\verb!dAb3bAd!\) 或 \(\verb!Adb3bdA!\),但是插入少于 \(2\) 个的字符无法变成回文词。
注意:此问题区分大小写。
输入格式
输入共一行,一个字符串。
输出格式
有且只有一个整数,即最少插入字符数。
输入输出样例 #1
输入 #1
Ab3bd
输出 #1
2
说明/提示
数据范围及约定
记字符串长度为 \(l\)。
对于全部数据,\(0<l\le 1000\)。
解法&&个人感想
那么,这题就是把单序列和多序列联系在一起的十分巧妙的题目
说一下我的解题历程吧,一开始我是考虑\(dp[i][j]\)是\([i,j]\)中需要插入的字符数,但是我发现转移方程是错误的,于是我想了挺久
举了一些例子,突然想到,既然回文子串的定义是从左往右看相等,那我把原字符串反转,取它的最长公共子序列,再减去不就好了!然后就做完了
有一种题解给出的做法:对于\([i,j]\),若\(s[i]==s[j]\)则说明串的两头相等,不需要再插入
如果\(s[i]!=s[j]\),说明串的两头不同,需要插入一个来保持回文性质
这个也挺妙,就是做的时候没想到
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 1005
using namespace std;
string a;
int dp[maxn][maxn];
char c[maxn];
char fc[maxn];
const int INF=1e9;
int main(){
cin>>a;
int l=a.length();
for(int i=1;i<=l;i++){
c[i]=a[i-1];
}
for(int i=1;i<=l;i++){
fc[i]=c[l+1-i];
}
for(int i=1;i<=l;i++){
for(int j=1;j<=l;j++){
if(c[i]==fc[j]) dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);
dp[i][j]=max(dp[i][j],max(dp[i-1][j],dp[i][j-1]));
}
}
cout<<l-dp[l][l]<<endl;
system("pause");
return 0;
}
P1004 [NOIP 2000 提高组] 方格取数
题目背景
NOIP 2000 提高组 T4
题目描述
设有 \(N \times N\) 的方格图 \((N \le 9)\),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 \(0\)。如下图所示(见样例):
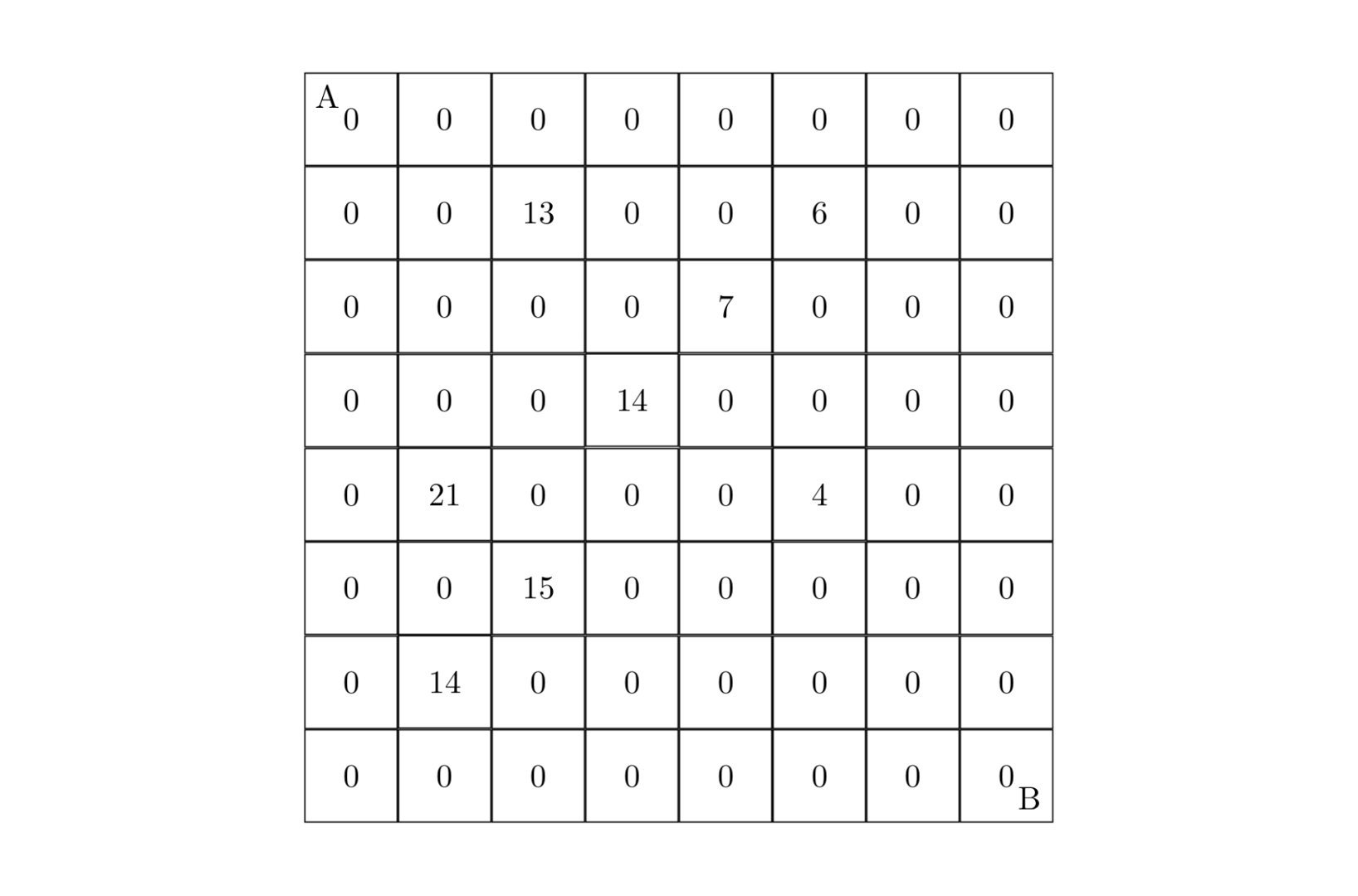
某人从图的左上角的 \(A\) 点出发,可以向下行走,也可以向右走,直到到达右下角的 \(B\) 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 \(0\))。
此人从 \(A\) 点到 \(B\) 点共走两次,试找出 \(2\) 条这样的路径,使得取得的数之和为最大。
输入格式
输入的第一行为一个整数 \(N\)(表示 \(N \times N\) 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 \(0\) 表示输入结束。
输出格式
只需输出一个整数,表示 \(2\) 条路径上取得的最大的和。
输入输出样例 #1
输入 #1
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出 #1
67
说明/提示
数据范围:\(1\le N\le 9\)。
解法&&个人感想
这道题是今天想不出来的题,锅还是出在数组定义
这里要重申一次,我们按照给定的数据返回,考虑数组的维数
目前,我见过的最多也就4维
这道题,刚好4维绰绰有余
那么,我一开始想的三维\(dp[i][j][k]\)表示\([i,j]\)被到达\(k\)次时的最大值
事实证明,这样转移方程不好写
所以,我看了题解之后,发现应该这样考虑这道题
把两条路径不要当做前后脚,而要当做两个人同时开始走
这样,我们就可以考虑两个人同时到达的数组\(dp[i][j][k][v]\)表示一个人到达\([i,j]\),另一个人到达\([k,v]\)的最大值
如果要优化,那么容易看出\(i+j=k+v\),所以可以优化成三维的
剩下的就不难
所以,数据范围小的时候,要大胆一点
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 15
using namespace std;
ll dp[maxn][maxn][maxn][maxn];
ll ma[maxn][maxn];
ll n;
ll x,y,op;
int main(){
cin>>n;
while(cin>>x>>y>>op){
if(x==0&&y==0&&op==0) break;
ma[x][y]=op;
}
dp[1][1][1][1]=ma[1][1];
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
for(int v=1;v<=n;v++){
dp[i][j][k][v]=max(max(dp[i-1][j][k][v-1],dp[i-1][j][k-1][v]),max(dp[i][j-1][k-1][v],dp[i][j-1][k][v-1]))+ma[i][j]+ma[k][v];
if(i==k&&j==v) dp[i][j][k][v]-=ma[i][j];
}
}
}
}
cout<<dp[n][n][n][n]<<endl;
system("pause");
return 0;
}
后半学期,也请各位继续关注:
《我的青春线代物语果然有问题》
《高数女主养成计划》
《程设の旅》
《青春猪头少年不会梦到多智能体吃豆人》
《某Linux的开源软件》
《Charlotte太空探索》
还有——
《我的算法竞赛不可能这么可爱》
本期到此结束!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号