【算法刷题】动态规划 Day1
最近打算把DP的题目再刷刷,这块算是最不熟的一块了
首先,我们先插播一下经过这一轮刷题,我对背包问题的理解
对于01背包,为什么我们用滚动数组进行优化的时候,需要倒序?而完全背包却是正序?
答:因为动态规划(\(Dynamic\) \(Programming\))对更新的要求是:要求更新时引用(不是cpp的引用)的值必须在之前被更新过,而在01背包中,第i个状态的更新是依赖于i-1状态的,如果滚动时采用正序,就会出现重复更新的情况(可以自己写一下转移方程),而在完全背包中,第i个状态的更新是依赖于第i个状态本身的,因此采用正向
完全背包,我们在参考代码的时候,发现滚动数组优化,j和k的顺序(即决策和状态)可以调换,目前不清楚是怎么一回事,不过,此时的状态需要倒序
然后我发现,当采用二维数组的时候,大多数时候都考虑正序而非倒序
混合背包,就直接把三种代码合在一起写
分组背包是我们比较不常见的,我们可以直接看下面的一道例题,即《金明的预算方案》
P2196 [NOIP 1996 提高组] 挖地雷
题目描述
在一个地图上有 \(N\ (N \le 20)\) 个地窖,每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后每次可以移动到一个编号比当前节点大且联通的节点去挖地雷,当无满足条件的节点时挖地雷工作结束。设计一个挖地雷的方案,使某人能挖到最多的地雷。
输入格式
有若干行。
第 \(1\) 行只有一个数字,表示地窖的个数 \(N\)。
第 \(2\) 行有 \(N\) 个数,分别表示每个地窖中的地雷个数。
第 \(3\) 行至第 \(N+1\) 行表示地窖之间的连接情况:
第 \(3\) 行有 \(n-1\) 个数(\(0\) 或 \(1\)),表示第一个地窖至第 \(2\) 个、第 \(3\) 个 \(\dots\) 第 \(n\) 个地窖有否路径连接。如第 \(3\) 行为 \(11000\cdots 0\),则表示第 \(1\) 个地窖至第 \(2\) 个地窖有路径,至第 \(3\) 个地窖有路径,至第 \(4\) 个地窖、第 \(5\) 个 \(\dots\) 第 \(n\) 个地窖没有路径。
第 \(4\) 行有 \(n-2\) 个数,表示第二个地窖至第 \(3\) 个、第 \(4\) 个 \(\dots\) 第 \(n\) 个地窖有否路径连接。
……
第 \(n+1\) 行有 \(1\) 个数,表示第 \(n-1\) 个地窖至第 \(n\) 个地窖有否路径连接。(为 \(0\) 表示没有路径,为 \(1\) 表示有路径)。
输出格式
第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个空格分隔,不得有多余的空格。
第二行只有一个数,表示能挖到的最多地雷数。
输入输出样例 #1
输入 #1
5
10 8 4 7 6
1 1 1 0
0 0 0
1 1
1
输出 #1
1 3 4 5
27
说明/提示
【样例解释】
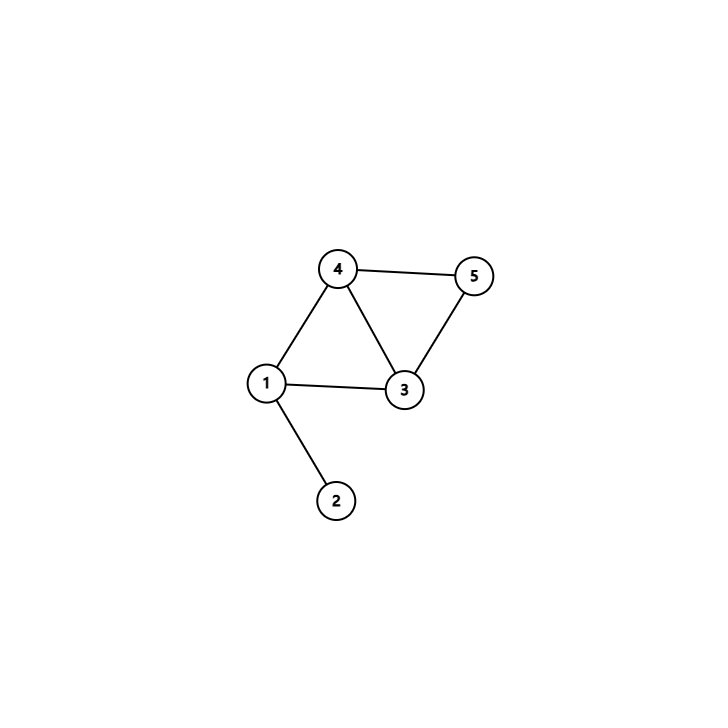
最优路径为 \(1 \to 3 \to 4 \to 5\),结果为 \(27\)。
【题目来源】
NOIP 1996 提高组第三题。
解法&&个人感想
我感觉转移方程其实应该都能推出来,但是比较关键的在于这个回溯的过程
一开始是想着用搜索,但是显而易见,这个栈的深度太大以至于没有办法实现
所以,我们直接采用这个方法:记录被更新的点的前驱,然后在输出路径的时候直接导入每个点的前驱就可以了
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 25
using namespace std;
int ma[maxn];
int lt[maxn][maxn];
int n;
int dp[maxn];
int ans=0;
int maxx=0;
int pre[maxn];
stack<int>s;
void output(int x){
s.push(x);
if(pre[x]==0){
while(!s.empty()){
int t=s.top();s.pop();
cout<<t<<' ';
}
cout<<endl;
return ;
}
else output(pre[x]);
return ;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>ma[i];
}
for(int i=1;i<=n-1;i++){
for(int j=i+1;j<=n;j++){
cin>>lt[i][j];
}
}
for(int i=1;i<=n;i++){
dp[i]=ma[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=i-1;j++){
if(lt[j][i]){
if(dp[i]<dp[j]+ma[i]){
dp[i]=dp[j]+ma[i];
pre[i]=j;
}
}
}
}
for(int i=1;i<=n;i++){
if(dp[i]>ans){
ans=dp[i];
maxx=i;
}
}
output(maxx);
cout<<ans<<endl;
system("pause");
return 0;
}
P1434 [SHOI2002] 滑雪
题目描述
Michael 喜欢滑雪。这并不奇怪,因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子:
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度会减小。在上面的例子中,一条可行的滑坡为 \(24-17-16-1\)(从 \(24\) 开始,在 \(1\) 结束)。当然 \(25\)-\(24\)-\(23\)-\(\ldots\)-\(3\)-\(2\)-\(1\) 更长。事实上,这是最长的一条。
输入格式
输入的第一行为表示区域的二维数组的行数 \(R\) 和列数 \(C\)。下面是 \(R\) 行,每行有 \(C\) 个数,代表高度(两个数字之间用 \(1\) 个空格间隔)。
输出格式
输出区域中最长滑坡的长度。
输入输出样例 #1
输入 #1
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
输出 #1
25
说明/提示
对于 \(100\%\) 的数据,\(1\leq R,C\leq 100\)。
解法&&个人感想
这里我就想着,我们如果要从某个点开始进行dp,由于dp的无后效性,我们应该选哪个点开始呢?
从上题看,我还真有将每个点排序,然后连边的想法,但是这个很快被打破了
为啥?因为可能有高度相等的节点
此时,我们就思考,有没有更好的方式?
那就是,记录每个点的高度,用结构体做题
转移的时候再判断每个点是否能被更新,这样也是把原来的路径链式化的一种套路
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 110
using namespace std;
struct node{
int x,y,h;
bool operator<(const node &other){
return h>other.h;
}
}ma[maxn*maxn];
int dp[maxn*maxn];
int n,m;
int ans=1;
bool check(int x,int y){
int ax=ma[x].x,ay=ma[x].y;
int bx=ma[y].x,by=ma[y].y;
if(ax==bx&&abs(ay-by)==1) return true;
if(abs(ax-bx)==1&&ay==by) return true;
return false;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>ma[(i-1)*m+j].h;
ma[(i-1)*m+j].x=i;
ma[(i-1)*m+j].y=j;
}
}
for(int i=1;i<=n*m;i++) dp[i]=1;
sort(ma+1,ma+1+n*m);
for(int i=n*m;i>=1;i--){
for(int j=i-1;j>=1;j--){
if(ma[i].h!=ma[j].h&&check(i,j)) dp[j]=max(dp[i]+1,dp[j]);
}
}
for(int i=1;i<=n*m;i++) ans=max(dp[i],ans);
cout<<ans<<endl;
system("pause");
return 0;
}
P4017 最大食物链计数
题目背景
你知道食物链吗?Delia 生物考试的时候,数食物链条数的题目全都错了,因为她总是重复数了几条或漏掉了几条。于是她来就来求助你,然而你也不会啊!写一个程序来帮帮她吧。
题目描述
给你一个食物网,你要求出这个食物网中最大食物链的数量。
(这里的“最大食物链”,指的是生物学意义上的食物链,即最左端是不会捕食其他生物的生产者,最右端是不会被其他生物捕食的消费者。)
Delia 非常急,所以你只有 \(1\) 秒的时间。
由于这个结果可能过大,你只需要输出总数模上 \(80112002\) 的结果。
输入格式
第一行,两个正整数 \(n、m\),表示生物种类 \(n\) 和吃与被吃的关系数 \(m\)。
接下来 \(m\) 行,每行两个正整数,表示被吃的生物A和吃A的生物B。
输出格式
一行一个整数,为最大食物链数量模上 \(80112002\) 的结果。
输入输出样例 #1
输入 #1
5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4
输出 #1
5
说明/提示
各测试点满足以下约定:
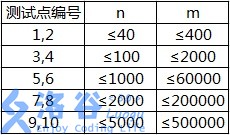
【补充说明】
数据中不会出现环,满足生物学的要求。(感谢 @AKEE )
解法&&个人感想
我们很容易看出这是一个DAG,在前面的讨论中,我们讲到DAG中作DP的方式是什么?
没错,是拓扑排序!
然后就完了,注意一下%的地方
注意:可能有多个入度为0的点和多个出度为0的点
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 5005
#define maxm 500005
using namespace std;
int n,m,tot;
int x,y;
int head[2*maxm],ver[2*maxm],nex[2*maxm];
int from[2*maxm];
int deg[maxn],vis[maxn],fdeg[maxn];
int dp[maxn];
int ans=0;
const int INF=80112002;
void add(int x,int y){
ver[++tot]=y;
from[tot]=x;
nex[tot]=head[x];
head[x]=tot;
deg[y]++;
fdeg[x]++;
return ;
}
void topsort(){
queue<int>q;
for(int i=1;i<=n;i++){
if(!deg[i]){
q.push(i);
dp[i]=1;
}
}
while(!q.empty()){
int x=q.front();q.pop();
for(int i=head[x];i;i=nex[i]){
int f=from[i];
int y=ver[i];
deg[y]--;
dp[y]+=dp[f]%INF;
dp[y]%=INF;
if(!deg[y]){
q.push(y);
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>x>>y;
add(x,y);
}
topsort();
for(int i=1;i<=n;i++){
if(!fdeg[i]) ans+=dp[i]%INF;
}
cout<<ans%INF<<endl;
system("pause");
return 0;
}
P1802 5 倍经验日
题目背景
现在乐斗有活动了!每打一个人可以获得 5 倍经验!absi2011 却无奈的看着那一些比他等级高的好友,想着能否把他们干掉。干掉能拿不少经验的。
题目描述
现在 absi2011 拿出了 \(x\) 个迷你装药物(嗑药打人可耻…),准备开始与那些人打了。
由于迷你装药物每个只能用一次,所以 absi2011 要谨慎的使用这些药。悲剧的是,用药量没达到最少打败该人所需的属性药药量,则打这个人必输。例如他用 \(2\) 个药去打别人,别人却表明 \(3\) 个药才能打过,那么相当于你输了并且这两个属性药浪费了。
现在有 \(n\) 个好友,给定失败时可获得的经验、胜利时可获得的经验,打败他至少需要的药量。
要求求出最大经验 \(s\),输出 \(5s\)。
输入格式
第一行两个数,\(n\) 和 \(x\)。
后面 \(n\) 行每行三个数,分别表示失败时获得的经验 \(\mathit{lose}_i\),胜利时获得的经验 \(\mathit{win}_i\) 和打过要至少使用的药数量 \(\mathit{use}_i\)。
输出格式
一个整数,最多获得的经验的五倍。
输入输出样例 #1
输入 #1
6 8
21 52 1
21 70 5
21 48 2
14 38 3
14 36 1
14 36 2
输出 #1
1060
说明/提示
【Hint】
五倍经验活动的时候,absi2011 总是吃体力药水而不是这种属性药。
【数据范围】
- 对于 \(10\%\) 的数据,保证 \(x=0\)。
- 对于 \(30\%\) 的数据,保证 \(0\le n\le 10\),\(0\le x\le 20\)。
- 对于 \(60\%\) 的数据,保证 \(0\le n,x\le 100\), \(10<lose_i,win_i\le 100\),\(0\le use_i\le 5\)。
- 对于 \(100\%\) 的数据,保证 \(0\le n,x\le 10^3\),\(0<lose_i\le win_i\le 10^6\),\(0\le use_i\le 10^3\)。
【题目来源】
fight.pet.qq.com
absi2011 授权题目
解法&&个人感想
这道题,其实也是01背包的变式,问题在于,我们要如何将打不过的状态进行更新
这里有一个tip:就是当当前状态打不过的时候,也要加上打不过的经验值,所以在状态转移的时候要分类讨论
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 1005
using namespace std;
ll n,x;
ll a[maxn],b[maxn],v[maxn];
ll dp[maxn];
int main(){
cin>>n>>x;
for(int i=1;i<=n;i++){
cin>>a[i]>>b[i]>>v[i];
}
for(int i=1;i<=n;i++){
for(int j=x;j>=v[i];j--){
dp[j]=max(dp[j-v[i]]+b[i],dp[j]+a[i]);
}
for(int j=v[i]-1;j>=0;j--){
dp[j]+=a[i];
}
}
cout<<5*dp[x]<<endl;
system("pause");
return 0;
}
P1164 小A点菜
题目背景
uim 神犇拿到了 uoi 的 ra(镭牌)后,立刻拉着基友小 A 到了一家……餐馆,很低端的那种。
uim 指着墙上的价目表(太低级了没有菜单),说:“随便点”。
题目描述
不过 uim 由于买了一些书,口袋里只剩 \(M\) 元 \((M \le 10000)\)。
餐馆虽低端,但是菜品种类不少,有 \(N\) 种 \((N \le 100)\),第 \(i\) 种卖 \(a_i\) 元 \((a_i \le 1000)\)。由于是很低端的餐馆,所以每种菜只有一份。
小 A 奉行“不把钱吃光不罢休”的原则,所以他点单一定刚好把 uim 身上所有钱花完。他想知道有多少种点菜方法。
由于小 A 肚子太饿,所以最多只能等待 \(1\) 秒。
输入格式
第一行是两个数字,表示 \(N\) 和 \(M\)。
第二行起 \(N\) 个正数 \(a_i\)(可以有相同的数字,每个数字均在 \(1000\) 以内)。
输出格式
一个正整数,表示点菜方案数,保证答案的范围在 int 之内。
输入输出样例 #1
输入 #1
4 4
1 1 2 2
输出 #1
3
说明/提示
2020.8.29,增添一组 hack 数据 by @yummy
解法&&个人感想
这道题的转移方程我就不提了,主要是在于这个赋初值的方式
为什么\(dp[0]=1\)?我想的是,当我们更新的时候,\(dp[j]+=dp[j-w[i]]\),当\(j=w[i]\)的时候,我们会发现,此时,应该代表的是,在第\(i\)道菜什么都不拿的决策,这也是一种决策,所以应该赋值为1
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 10005
#define maxm 10005
using namespace std;
int m,n;
int ma[maxn];
int dp[maxm];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>ma[i];
}
dp[0]=1;
for(int i=1;i<=n;i++){
for(int j=m;j>=ma[i];j--){
dp[j]+=dp[j-ma[i]];
}
}
cout<<dp[m]<<endl;
system("pause");
return 0;
}
P1077 [NOIP 2012 普及组] 摆花
题目描述
小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 \(m\) 盆。通过调查顾客的喜好,小明列出了顾客最喜欢的 \(n\) 种花,从 \(1\) 到 \(n\) 标号。为了在门口展出更多种花,规定第 \(i\) 种花不能超过 \(a_i\) 盆,摆花时同一种花放在一起,且不同种类的花需按标号的从小到大的顺序依次摆列。
试编程计算,一共有多少种不同的摆花方案。
输入格式
第一行包含两个正整数 \(n\) 和 \(m\),中间用一个空格隔开。
第二行有 \(n\) 个整数,每两个整数之间用一个空格隔开,依次表示 \(a_1,a_2, \cdots ,a_n\)。
输出格式
一个整数,表示有多少种方案。注意:因为方案数可能很多,请输出方案数对 \(10^6+7\) 取模的结果。
输入输出样例 #1
输入 #1
2 4
3 2
输出 #1
2
说明/提示
【数据范围】
对于 \(20\%\) 数据,有 \(0<n \le 8,0<m \le 8,0 \le a_i \le 8\)。
对于 \(50\%\) 数据,有 \(0<n \le 20,0<m \le 20,0 \le a_i \le 20\)。
对于 \(100\%\) 数据,有 \(0<n \le 100,0<m \le 100,0 \le a_i \le 100\)。
NOIP 2012 普及组 第三题
解法&&个人感想
我本来以为这道题是多重背包,可以使用二进制优化
但是,样例让我意识到了,二进制优化,当物品数量为2的次幂的时候,会很麻烦
于是,我还是使用了二重数组
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 105
#define maxm 205
using namespace std;
int n,m;
int ma[maxn];
int dp[maxn][maxm];
const int INF=1e6+7;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>ma[i];
}
dp[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=0;j<=ma[i];j++){
for(int k=j;k<=m;k++){
dp[i][k]+=dp[i-1][k-j]%INF;
dp[i][k]%=INF;
}
}
}
cout<<dp[n][m]%INF<<endl;
system("pause");
return 0;
}
(还像我之前说的一样,多重背包好像j和k可以互换,现在不知道为啥)
这是另一种解法,来源:洛谷题解区
#include<bits/stdc++.h>
using namespace std;
const int maxn=105, mod = 1000007;
int n, m, a[maxn], f[maxn];
int main()
{
cin>>n>>m;
for(int i=1; i<=n; i++) cin>>a[i];
f[0] = 1;
for(int i=1; i<=n; i++)
for(int j=m; j>=0; j--) //注意,是01背包
for(int k=1; k<=min(a[i], j); k++)
f[j] = (f[j] + f[j-k])%mod;
cout<<f[m]<<endl;
return 0;
}
P1064 [NOIP 2006 提高组] 金明的预算方案
题目描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 \(n\) 元钱就行”。今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
| 主件 | 附件 |
|---|---|
| 电脑 | 打印机,扫描仪 |
| 书柜 | 图书 |
| 书桌 | 台灯,文具 |
| 工作椅 | 无 |
如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有 \(0\) 个、\(1\) 个或 \(2\) 个附件。每个附件对应一个主件,附件不再有从属于自己的附件。金明想买的东西很多,肯定会超过妈妈限定的 \(n\) 元。于是,他把每件物品规定了一个重要度,分为 \(5\) 等:用整数 \(1 \sim 5\) 表示,第 \(5\) 等最重要。他还从因特网上查到了每件物品的价格(都是 \(10\) 元的整数倍)。他希望在不超过 \(n\) 元的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 \(j\) 件物品的价格为 \(v_j\),重要度为 \(w_j\),共选中了 \(k\) 件物品,编号依次为 \(j_1,j_2,\dots,j_k\),则所求的总和为:
请你帮助金明设计一个满足要求的购物单。
输入格式
第一行有两个整数,分别表示总钱数 \(n\) 和希望购买的物品个数 \(m\)。
第 \(2\) 到第 \((m + 1)\) 行,每行三个整数,第 \((i + 1)\) 行的整数 \(v_i\),\(p_i\),\(q_i\) 分别表示第 \(i\) 件物品的价格、重要度以及它对应的的主件。如果 \(q_i=0\),表示该物品本身是主件。
输出格式
输出一行一个整数表示答案。
输入输出样例 #1
输入 #1
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
输出 #1
2200
说明/提示
数据规模与约定
对于全部的测试点,保证 \(1 \leq n \leq 3.2 \times 10^4\),\(1 \leq m \leq 60\),\(0 \leq v_i \leq 10^4\),\(1 \leq p_i \leq 5\),\(0 \leq q_i \leq m\),答案不超过 \(2 \times 10^5\)。
NOIP 2006 提高组 第二题
解法&&个人感想
这道题,因为给定了我们分组的个数,可以视为分组背包
如果不限的话,就是树上背包了
我们直接看吧
就是个模板
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxm 100005
#define maxn 1005
using namespace std;
struct node{
int tot;
int pd;
int t[5];
int v[5];
}temp[maxm];
node ma[maxm];
int n,m,cnt;
int x,y,op;
int v[maxm];
int w[maxm];
int dp[maxm];
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>x>>y>>op;
if(op){
if(temp[op].pd==0){
if(temp[op].tot==0){
temp[op].tot=2;
}
else{
temp[op].tot++;
}
temp[op].t[temp[op].tot]=x*y;
temp[op].v[temp[op].tot]=x;
}
else{
temp[op].tot++;
temp[op].t[temp[op].tot]=x*y;
temp[op].v[temp[op].tot]=x;
}
}
else{
if(temp[i].tot==0) temp[i].tot++;
temp[i].pd=1;
temp[i].t[1]=x*y;
temp[i].v[1]=x;
}
}
for(int i=1;i<=m;i++){
if(temp[i].tot==0) continue;
cnt++;
if(temp[i].tot==1){
ma[cnt].tot=1;
ma[cnt].t[1]=temp[i].t[1];
ma[cnt].v[1]=temp[i].v[1];
}
else if(temp[i].tot==2){
ma[cnt].tot=2;
ma[cnt].t[1]=temp[i].t[1];
ma[cnt].t[2]=temp[i].t[1]+temp[i].t[2];
ma[cnt].v[1]=temp[i].v[1];
ma[cnt].v[2]=temp[i].v[2]+temp[i].v[1];
}
else if(temp[i].tot==3){
ma[cnt].tot=4;
ma[cnt].t[1]=temp[i].t[1];
ma[cnt].t[2]=temp[i].t[1]+temp[i].t[2];
ma[cnt].t[3]=temp[i].t[1]+temp[i].t[3];
ma[cnt].t[4]=temp[i].t[1]+temp[i].t[2]+temp[i].t[3];
ma[cnt].v[1]=temp[i].v[1];
ma[cnt].v[2]=temp[i].v[1]+temp[i].v[2];
ma[cnt].v[3]=temp[i].v[1]+temp[i].v[3];
ma[cnt].v[4]=temp[i].v[1]+temp[i].v[2]+temp[i].v[3];
}
}
for(int i=1;i<=cnt;i++){
for(int j=n;j>=0;j--){
for(int k=1;k<=ma[i].tot;k++){
if(j>=ma[i].v[k]) dp[j]=max(dp[j],dp[j-ma[i].v[k]]+ma[i].t[k]);
}
}
}
cout<<dp[n]<<endl;
system("pause");
return 0;
}
P3842 [TJOI2007] 线段
题目描述
在一个 \(n \times n\) 的平面上,在每一行中有一条线段,第 \(i\) 行的线段的左端点是 \((i, L_{i})\),右端点是 \((i, R_{i})\)。
你从 \((1,1)\) 点出发,要求沿途走过所有的线段,最终到达 \((n,n)\) 点,且所走的路程长度要尽量短。
更具体一些说,你在任何时候只能选择向下走一步(行数增加 \(1\))、向左走一步(列数减少 \(1\))或是向右走一步(列数增加 \(1\))。当然,由于你不能向上行走,因此在从任何一行向下走到另一行的时候,你必须保证已经走完本行的那条线段。
输入格式
第一行有一个整数 \(n\)。
以下 \(n\) 行,在第 \(i\) 行(总第 \((i+1)\) 行)的两个整数表示 \(L_i\) 和 \(R_i\)。
输出格式
仅包含一个整数,你选择的最短路程的长度。
输入输出样例 #1
输入 #1
6
2 6
3 4
1 3
1 2
3 6
4 5
输出 #1
24
说明/提示
我们选择的路线是
(1, 1) (1, 6)
(2, 6) (2, 3)
(3, 3) (3, 1)
(4, 1) (4, 2)
(5, 2) (5, 6)
(6, 6) (6, 4) (6, 6)
不难计算得到,路程的总长度是 \(24\)。
对于 \(100\%\) 的数据,\(1\le n \le 2 \times 10^4\),\(1 \le L_i \le R_i \le n\)。
解法&&个人感想
这道题,我在做的时候已经考虑到DP数组的设法了
然后就开始笨笨地列举出六种情况,归纳出转移方程
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 200005
using namespace std;
int l[maxn],r[maxn];
int n;
int dp[maxn][2]; //0表示在左边,1表示在右边
int len[maxn];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>l[i]>>r[i];
len[i]=r[i]-l[i];
}
dp[1][0]=r[1]-1;
dp[1][1]=r[1]-1;
if(r[1]<=l[2]){
dp[2][0]=dp[1][1]+abs(r[2]-r[1])+len[2];
dp[2][1]=dp[1][1]+abs(r[2]-l[1]);
}
else if(r[1]>l[2]&&r[1]<r[2]){
dp[2][0]=dp[1][1]+abs(r[2]-r[1])+len[2];
dp[2][1]=dp[1][1]+abs(l[2]-r[1])+len[2];
}
else if(r[1]>=r[2]){
dp[2][0]=dp[1][1]+abs(l[2]-r[1]);
dp[2][1]=dp[1][1]+abs(l[2]-r[1])+len[2];
}
for(int i=3;i<=n;i++){
if(l[i-1]<=l[i]){
dp[i][1]=dp[i-1][0]+abs(r[i]-l[i-1]);
}
else{
dp[i][1]=dp[i-1][0]+abs(l[i]-l[i-1])+len[i];
}
if(l[i-1]<=r[i]){
dp[i][0]=dp[i-1][0]+abs(r[i]-l[i-1])+len[i];
}
else{
dp[i][0]=dp[i-1][0]+abs(l[i]-l[i-1]);
}
if(r[i-1]<=r[i]){
dp[i][0]=min(dp[i][0],dp[i-1][1]+abs(r[i]-r[i-1])+len[i]);
}
else{
dp[i][0]=min(dp[i][0],dp[i-1][1]+abs(l[i]-r[i-1]));
}
if(r[i-1]>=l[i]){
dp[i][1]=min(dp[i][1],dp[i-1][1]+abs(l[i]-r[i-1])+len[i]);
}
else{
dp[i][1]=min(dp[i][1],dp[i-1][1]+abs(r[i]-r[i-1]));
}
}
cout<<min(dp[n][0]+abs(n-l[n]),dp[n][1]+abs(n-r[n]))+n-1<<endl;
system("pause");
return 0;
}
然而答案的解法更简单
我们注意到,如果要覆盖一条线段,那么到一个端点,一定是从另一个端点过来的
所以,只需要计算上一层的两个端点到另一个端点的距离,加上这一层的长度就可以
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 200005
using namespace std;
int l[maxn],r[maxn];
int dp[maxn][2];
int len[maxn];
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>l[i]>>r[i];
len[i]=r[i]-l[i];
}
dp[1][0]=r[1]-1+len[1];
dp[1][1]=r[1]-1;
for(int i=2;i<=n;i++){
dp[i][0]=min(dp[i-1][0]+abs(r[i]-l[i-1])+len[i],dp[i-1][1]+abs(r[i]-r[i-1])+len[i]);
dp[i][1]=min(dp[i-1][0]+abs(l[i]-l[i-1])+len[i],dp[i-1][1]+abs(l[i]-r[i-1])+len[i]);
}
cout<<min(dp[n][0]+n-l[n],dp[n][1]+n-r[n])+n-1<<endl;
system("pause");
return 0;
}
后半学期,也请各位继续关注:
《我的青春线代物语果然有问题》
《高数女主养成计划》
《程设の旅》
《青春猪头少年不会梦到多智能体吃豆人》
《某Linux的开源软件》
《Charlotte太空探索》
还有——
《我的算法竞赛不可能这么可爱》
本期到此结束!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号