【新算法学习】线段树,从入坑到入坟
今天,我们来学习线段树
某种意义上这确实算是数据结构里非常优美(甚至可以说是最优美?)的数据结构了
简约的分形美,比树状数组直观很多,处理范围也比较广
具体原理我就不讲了,你只需要知道
这棵树是一棵除了叶节点其他层都是完全二叉树的树
所以,我们在开数组的时候要注意,需要开\(4 \times n\)大的数组
然后,我们介绍一下几种基本操作
1.建树
struct SegmentTree{
ll l,r;
ll sum;
};
SegmentTree tree[4*maxn];
void build(ll n,ll l,ll r){
tree[n].l=l;tree[n].r=r;
if(l==r){
tree[n].sum=ma[l];
return ;
}
int mid=(l+r)/2;
build(n*2,l,mid);
build(n*2+1,mid+1,r);
tree[n].sum=tree[n*2].sum+tree[n*2+1].sum;
return ;
}
就是说,我们在建树的时候,需要递归往下建树(对一个节点,建立它的左子树和右子树)
然后,最后要实现一个pull操作,也就是从底层递推回根节点的时候,需要恢复逐层父节点的状态
然后,因为我们把根节点作为整个线段树的入口,所以,最后就直接\(build(1,1,n)\)就可以了
2.单点修改
这个其实不难,我们只需要逐层递归,找到我们需要修改的点,然后将它修改完即可
注意:在返回根节点的过程中仍需要进行一个pull操作,确保路径上的全部节点都受到修改了
void change(ll n,ll x,ll k){
if(tree[n].l==tree[n].r){
tree[n].sum+=k;
return ;
}
int mid=(tree[n].l+tree[n].r)/2;
if(x<=mid) change(n*2,x,k);
else change(n*2+1,x,k);
tree[n].sum=tree[n*2].sum+tree[n*2+1].sum;
}
每次,在主函数中调用\(change(1,x,k)\),其中\(x\)是被修改的节点,\(k\)是修改的值
我们还是那句话,把根节点作为整个线段树的入口,从而将整个线段树进行更新
3.区间查询
这个可能会有点难以理解,我先讲一下流程
\(1.\),若\(tree[x].l \le l\)且\(tree[x].r \le r\)时,此时我们可以将整个\(tree[x].sum\)纳入查询操作中
\(2.\),若\(l \le mid\),则\(sum\)会对其左子树进行查询
\(3.\),若\(mid < r\),则\(sum\)会对右子树进行查询
为什么?我们参考了《算法竞赛进阶指南》里的解释:
\(1.l \le tree[x].l \le tree[x].r \le r\),即完全覆盖了当前节点,因此直接返回(意思是,我们把所求区间化成多个线段树中的小区间求和)
\(2. tree[x].l \le l \le tree[x].r \le r\),只有\(l\)位于节点之内
\((1). l>mid\),只会遍历右子树
$(2). l \le mid $,此时会递归两棵子树,但是,右子树完全覆盖,因此直接返回
\(3. l \le tree[x].l \le r \le tree[x].r\),即只有\(r\)位于节点之内,与上述情况类似。
\(4. tree[x].l \le l \le r \le tree[x].r\),即\(l\)和\(r\)都位于节点之内
$(1). $ \(l,r\)都位于\(mid\)的同一侧,此时只会递归一棵子树
$(2). $ \(l,r\)分别位于\(mid\)的两侧,此时递归左右两棵子树
综上,我们可以合并出上述法则
然后,我们把代码放出来:
ll query(ll n,ll l,ll r){
if(l<=tree[n].l&&tree[n].r<=r) return tree[n].sum;
int mid=(tree[n].l+tree[n].r)/2;
ll ans=0;
if(l<=mid) ans+=query(n*2,l,r);
if(r>mid) ans+=query(n*2+1,l,r);
return ans;
}
注意,这里的\(l\)和\(r\)跟在上述函数中不一样,是不会变的
在主函数中的调用入口为\(query(1,l,r)\)
还是那句话,根节点是我们的引入点,这点毋庸置疑
下面我们从一道例题看这个问题:
P3374 【模板】树状数组 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 \(x\)
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 \(n,m\),分别表示该数列数字的个数和操作的总个数。
第二行包含 \(n\) 个用空格分隔的整数,其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。
接下来 \(m\) 行每行包含 \(3\) 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 \(x\) 个数加上 \(k\) -
2 x y含义:输出区间 \([x,y]\) 内每个数的和
输出格式
输出包含若干行整数,即为所有操作 \(2\) 的结果。
输入输出样例 #1
输入 #1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
输出 #1
14
16
说明/提示
【数据范围】
对于 \(30\%\) 的数据,\(1 \le n \le 8\),\(1\le m \le 10\);
对于 \(70\%\) 的数据,\(1\le n,m \le 10^4\);
对于 \(100\%\) 的数据,\(1\le n,m \le 5\times 10^5\)。
数据保证对于任意时刻,\(a\) 的任意子区间(包括长度为 \(1\) 和 \(n\) 的子区间)和均在 \([-2^{31}, 2^{31})\) 范围内。
样例说明:
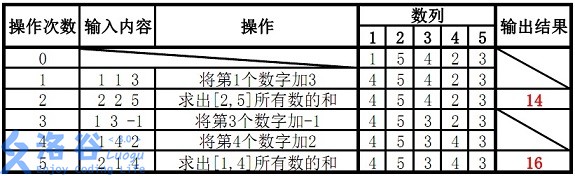
故输出结果14、16
解法&&个人感想
没错,还是这题
事实上线段树在思维难度上某种意义来说比树状数组更简单
因为比较直观
但是码量可能就比较多了
我们直接看代码吧,毕竟就是上面几种操作合在一起
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 500005
using namespace std;
struct SegmentTree{
ll l,r;
ll sum;
};
SegmentTree tree[4*maxn];
ll n,m,op,x,y,k;
ll ma[maxn];
void build(ll n,ll l,ll r){
tree[n].l=l;tree[n].r=r;
if(l==r){
tree[n].sum=ma[l];
return ;
}
int mid=(l+r)/2;
build(n*2,l,mid);
build(n*2+1,mid+1,r);
tree[n].sum=tree[n*2].sum+tree[n*2+1].sum;
return ;
}
void change(ll n,ll x,ll k){
if(tree[n].l==tree[n].r){
tree[n].sum+=k;
return ;
}
int mid=(tree[n].l+tree[n].r)/2;
if(x<=mid) change(n*2,x,k);
else change(n*2+1,x,k);
tree[n].sum=tree[n*2].sum+tree[n*2+1].sum;
}
ll query(ll n,ll l,ll r){
if(l<=tree[n].l&&tree[n].r<=r) return tree[n].sum;
int mid=(tree[n].l+tree[n].r)/2;
ll ans=0;
if(l<=mid) ans+=query(n*2,l,r);
if(r>mid) ans+=query(n*2+1,l,r);
return ans;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>ma[i];
}
build(1,1,n);
for(int i=1;i<=m;i++){
cin>>op;
if(op==1){
cin>>x>>k;
change(1,x,k);
ma[x]+=k;
}
else{
cin>>x>>y;
ll ans=query(1,x,y);
cout<<ans<<endl;
}
}
system("pause");
return 0;
}
4.区间修改
我们这里需要介绍一个叫延迟标记(又称懒标记,Lazymark)的东西
为什么要有这个东西?我参考了一下《算法竞赛进阶指南》里的解释:
大概的意思是:如果某个节点被区间\([l,r]\)完全覆盖,那么以该节点为根的整棵子树中的所有节点存储的信息都会发生变化,若逐一进行更新,将使得一次区间修改指令的时间复杂度增加到\(O(N)\),这是我们不能接受的。
那么,这个的原理是什么呢?
我们在执行修改指令时,如果对子树逐一进行修改操作,如果最终查询时却发现根本没有用到它作为候选答案,那么这就是徒劳的。
为了优化这种情况,我们引入了延迟标记,在执行修改指令时,可以在\(l \le p_l \le p_r \le r\)的情况下立即返回,在回溯之前向节点\(p\)增加一个标记,标识“该节点曾经被修改,但其子节点尚未被更新”。
于是,我们有了一个\(pushdown\)的操作
void pushdown(ll x){
if(tree[x].add){
tree[x*2].add+=tree[x].add;
tree[x*2+1].add+=tree[x].add;
tree[x*2].sum+=(tree[x*2].r-tree[x*2].l+1)*tree[x].add;
tree[x*2+1].sum+=(tree[x*2+1].r-tree[x*2+1].l+1)*tree[x].add;
tree[x].add=0;
}
return ;
}
然后,我们的区间修改函数,跟区间查询函数有点像
void change(ll x,ll l,ll r,ll k){
if(l<=tree[x].l&&tree[x].r<=r){
tree[x].sum+=k*(tree[x].r-tree[x].l+1);
tree[x].add+=k;
return ;
}
int mid=(tree[x].l+tree[x].r)/2;
pushdown(x);
if(l<=mid) change(x*2,l,r,k);
if(r>mid) change(x*2+1,l,r,k);
tree[x].sum=tree[x*2].sum+tree[x*2+1].sum;
return ;
}
这里我们还是以一道题为例
P3373 【模板】线段树 2
题目描述
如题,已知一个数列,你需要进行下面三种操作:
- 将某区间每一个数乘上 \(x\);
- 将某区间每一个数加上 \(x\);
- 求出某区间每一个数的和。
输入格式
第一行包含三个整数 \(n,q,m\),分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 \(n\) 个用空格分隔的整数,其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。
接下来 \(q\) 行每行包含若干个整数,表示一个操作,具体如下:
操作 \(1\): 格式:1 x y k 含义:将区间 \([x,y]\) 内每个数乘上 \(k\)
操作 \(2\): 格式:2 x y k 含义:将区间 \([x,y]\) 内每个数加上 \(k\)
操作 \(3\): 格式:3 x y 含义:输出区间 \([x,y]\) 内每个数的和对 \(m\) 取模所得的结果
输出格式
输出包含若干行整数,即为所有操作 \(3\) 的结果。
输入输出样例 #1
输入 #1
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
输出 #1
17
2
说明/提示
【数据范围】
对于 \(30\%\) 的数据:\(n \le 8\),\(q \le 10\)。
对于 \(70\%\) 的数据:$n \le 10^3 \(,\)q \le 10^4$。
对于 \(100\%\) 的数据:\(1 \le n \le 10^5\),\(1 \le q \le 10^5\)。
除样例外,\(m = 571373\)。
(数据已经过加强 _)
样例说明:
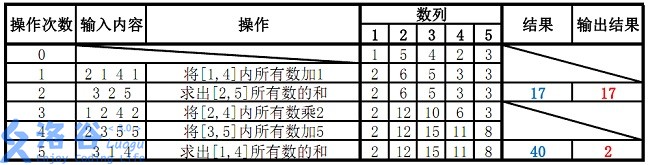
故输出应为 \(17\)、\(2\)(\(40 \bmod 38 = 2\))。
解法&&个人感想
我直接把线段树2放上来,要说明的是,我们怎么在多个连续值的传递下做出正确的传递操作
思路:按照正常的乘法和加法思路来,如果一个数可能同时拥有加和乘两个标记,那么,我们肯定优先处理的还是乘法标记,同时,加法标记也要乘上这个乘法标记的值
然后,思路就比较明朗了
注意:无论是哪里都要模一个m,乘法标记也要
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 100005
using namespace std;
struct SegmentTree{
ll l,r;
ll mul,add;
ll sum;
}tree[4*maxn];
ll n,q,m;
ll op,x,y,k;
ll ma[maxn];
void build(ll x,ll l,ll r){
tree[x].l=l;tree[x].r=r;
if(tree[x].l==tree[x].r){
tree[x].sum=ma[l]%m;
return ;
}
ll mid=(tree[x].l+tree[x].r)/2;
build(x*2,l,mid);
build(x*2+1,mid+1,r);
tree[x].sum=(tree[x*2].sum%m+tree[x*2+1].sum%m)%m;
return ;
}
void pushdown(ll x){
tree[x*2].add=((tree[x*2].add*tree[x].mul)%m+tree[x].add)%m;
tree[x*2+1].add=((tree[x*2+1].add*tree[x].mul)%m+tree[x].add)%m;
tree[x*2].mul=tree[x*2].mul*tree[x].mul%m;
tree[x*2+1].mul=tree[x*2+1].mul*tree[x].mul%m;
tree[x*2].sum=((tree[x*2].sum*tree[x].mul)%m+(tree[x].add*(tree[x*2].r-tree[x*2].l+1))%m)%m;
tree[x*2+1].sum=((tree[x*2+1].sum*tree[x].mul)%m+(tree[x].add*(tree[x*2+1].r-tree[x*2+1].l+1))%m)%m;
tree[x].add=0;
tree[x].mul=1;
return ;
}
void change(ll x,ll l,ll r,ll add,ll mul){
if(l<=tree[x].l&&tree[x].r<=r){
tree[x].mul=tree[x].mul*mul%m;
tree[x].add=((tree[x].add*mul)%m+add)%m;
tree[x].sum=(((tree[x].sum%m)*mul)%m+add*(tree[x].r-tree[x].l+1))%m;
return ;
}
ll mid=(tree[x].l+tree[x].r)/2;
pushdown(x);
if(l<=mid) change(x*2,l,r,add,mul);
if(r>mid) change(x*2+1,l,r,add,mul);
tree[x].sum=(tree[x*2].sum%m+tree[x*2+1].sum%m)%m;
return ;
}
ll query(ll x,ll l,ll r){
if(l<=tree[x].l&&tree[x].r<=r) return tree[x].sum%m;
ll mid=(tree[x].l+tree[x].r)/2;
ll ans=0;
pushdown(x);
if(l<=mid) ans+=query(x*2,l,r)%m;
if(r>mid) ans+=query(x*2+1,l,r)%m;
return ans;
}
int main(){
cin>>n>>q>>m;
for(int i=1;i<=4*n;i++) tree[i].mul=1;
for(int i=1;i<=n;i++){
cin>>ma[i];
ma[i]%=m;
}
build(1,1,n);
for(int i=1;i<=q;i++){
cin>>op;
if(op==1){
cin>>x>>y>>k;
change(1,x,y,0,k);
}
else if(op==2){
cin>>x>>y>>k;
change(1,x,y,k,1);
}
else{
cin>>x>>y;
ll ans=query(1,x,y)%m;
cout<<ans<<endl;
}
}
system("pause");
return 0;
}
后续还会更新,介绍延迟标记、区间修改等等操作
后半学期,也请各位继续关注:
《我的青春线代物语果然有问题》
《高数女主养成计划》
《程设の旅》
《青春猪头少年不会梦到多智能体吃豆人》
《某Linux的开源软件》
《Charlotte太空探索》
还有——
《我的算法竞赛不可能这么可爱》
本期到此结束!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号