【新算法学习】数据结构の树状数组
好久没有学新算法了!
五一刚好有空 虽然cf那边也要补题,但是不学新算法终究思路拓不开吧
今天复习了一下几年前学的树状数组
我们从一道题开始:
P3374 【模板】树状数组 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 \(x\)
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 \(n,m\),分别表示该数列数字的个数和操作的总个数。
第二行包含 \(n\) 个用空格分隔的整数,其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。
接下来 \(m\) 行每行包含 \(3\) 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 \(x\) 个数加上 \(k\) -
2 x y含义:输出区间 \([x,y]\) 内每个数的和
输出格式
输出包含若干行整数,即为所有操作 \(2\) 的结果。
输入输出样例 #1
输入 #1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
输出 #1
14
16
说明/提示
【数据范围】
对于 \(30\%\) 的数据,\(1 \le n \le 8\),\(1\le m \le 10\);
对于 \(70\%\) 的数据,\(1\le n,m \le 10^4\);
对于 \(100\%\) 的数据,\(1\le n,m \le 5\times 10^5\)。
数据保证对于任意时刻,\(a\) 的任意子区间(包括长度为 \(1\) 和 \(n\) 的子区间)和均在 \([-2^{31}, 2^{31})\) 范围内。
样例说明:
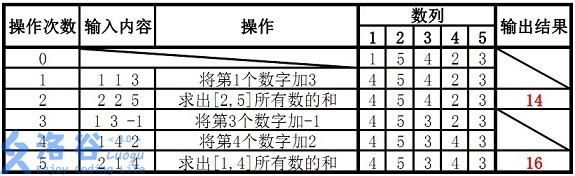
故输出结果14、16
Solution
在开始介绍树状数组之前,我们要介绍一下一种操作:\(lowbit\)
意思是,如果对于正整数\(x\),取它的二进制分解:
\(x=2^{i_1}+2^{i_2}+\ldots+2^{i_n}(0 \le i_1 < i_2 \ldots <i_n)\)
那么,\(lowbit(x)=2^{i_1}\)
说得挺简单,但是在程序中我们怎么实现它呢?
有的人说,这个简单,就是\(x\&(-x)\)
好了,为什么是\(x\&(-x)\)?
我们先介绍补码的概念,在C++中,众所周知,第一位是表示符号的位置,而补码确实在十进制中可以代表\(x\)的相反数,但它在二进制中则是对\(x\)的每位取反,然后再加一
打个比方 我们举5的例子
\((5)_{10}=(0\ldots101)_{2}\)
则\({(-5)_{10}=(1\ldots011)_{2}}\)
此时\(5 \& (-5)=1\)
也就是说\(lowbit(x)=x \& (-x)\)
然后,我们可以通过二进制分解对某个x分块
即\(1\Longrightarrow2^{i_1},2^{i_1}+1\Longrightarrow2^{i_2}\ldots\)
分成x的二进制分解中1的个数块
这样就形成了树的结构,\(tree[x]\)表示区间下标在\([x-lowbit(x)+1,x]\)中元素的和
现在,我要宣布,树状数组可以实现的功能主要有两个:定点添加和区间查找
对于区间查找,有一个类似前缀和的功能,毕竟只需将上述分段中每段的和加起来,就能求得\([1,x]\)中的和,然后取前缀和相减即可
代码如下:
int query(int x){
int ans=0;
while(x){
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}
定点添加,由于它的树状结构,只需要将其的祖先节点(包括它自己),同时加上x的值就可以,因为刚好这样就能够遍历后面的全部节点(分段求和阶段),这个自己证一下是不难的
代码如下:
void update(int x,int k){
while(x<=n){
tree[x]+=k;
x+=lowbit(x);
}
return ;
}
然后我们把代码拼起来就可以了:
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 500005
#define maxm 500005
using namespace std;
int tree[maxn];
int n,m;
int op,x,y,d;
int query(int x){
int ans=0;
while(x){
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}
void update(int x,int k){
while(x<=n){
tree[x]+=k;
x+=lowbit(x);
}
return ;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
cin>>d;
update(i,d);
}
for(int i=1;i<=m;i++){
cin>>op>>x>>y;
if(op==1){
update(x,y);
}
else{
cout<<query(y)-query(x-1)<<endl;
}
}
system("pause");
return 0;
}
然后看第二道
P3368 【模板】树状数组 2
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某区间每一个数加上 \(x\);
-
求出某一个数的值。
输入格式
第一行包含两个整数 \(N\)、\(M\),分别表示该数列数字的个数和操作的总个数。
第二行包含 \(N\) 个用空格分隔的整数,其中第 \(i\) 个数字表示数列第 $i $ 项的初始值。
接下来 \(M\) 行每行包含 \(2\) 或 \(4\)个整数,表示一个操作,具体如下:
操作 \(1\): 格式:1 x y k 含义:将区间 \([x,y]\) 内每个数加上 \(k\);
操作 \(2\): 格式:2 x 含义:输出第 \(x\) 个数的值。
输出格式
输出包含若干行整数,即为所有操作 \(2\) 的结果。
输入输出样例 #1
输入 #1
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4
输出 #1
6
10
说明/提示
样例 1 解释:
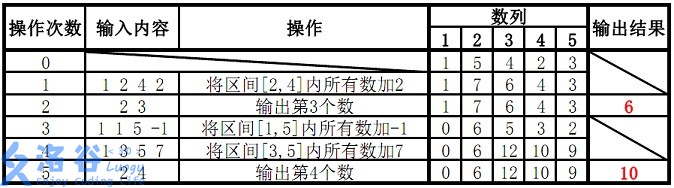
故输出结果为 6、10。
数据规模与约定
对于 \(30\%\) 的数据:\(N\le8\),\(M\le10\);
对于 \(70\%\) 的数据:\(N\le 10000\),\(M\le10000\);
对于 \(100\%\) 的数据:\(1 \leq N, M\le 500000\),\(1 \leq x, y \leq n\),保证任意时刻序列中任意元素的绝对值都不大于 \(2^{30}\)。
Solution
这里有用到差分的思想
既然我们能够实现定点添加和阶段求和,那么,为什么我们不能实现阶段添加和定点求和呢?
这两者在差分的意义上更像是相辅相成的
我们只需要将update中添加的元素换成\(a[i]-a[i-1]\)
然后update只需处理两个端点处的值,同时再求和的时候就是直接输出\(query(x)\)
下面看代码:
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 500005
#define maxm 500005
int n,m;
ll tree[maxn];
ll ma[maxn];
ll op,x,y,d,k;
using namespace std;
ll query(int x){
ll ans=0;
for(;x;x-=lowbit(x)) ans+=tree[x];
return ans;
}
void update(int x,ll k){
for(;x<=n;x+=lowbit(x)) tree[x]+=k;
return ;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
cin>>ma[i];
update(i,ma[i]-ma[i-1]);
}
for(int i=1;i<=m;i++){
cin>>op;
if(op==1){
cin>>x>>y>>k;
update(x,k);
update(y+1,-k);
}
else{
cin>>x;
cout<<query(x)<<endl;
}
}
system("pause");
return 0;
}
2025.05.07 补充
今天看了一下知乎,发现树状数组还有两种拓展
首先,我们介绍其中一种,区间增加&&区间查询
我们看一下这个题目(虽然是线段树1,但是树状数组也能做)
P3372 【模板】线段树 1
题目描述
如题,已知一个数列 \(\{a_i\}\),你需要进行下面两种操作:
- 将某区间每一个数加上 \(k\)。
- 求出某区间每一个数的和。
输入格式
第一行包含两个整数 \(n, m\),分别表示该数列数字的个数和操作的总个数。
第二行包含 \(n\) 个用空格分隔的整数 \(a_i\),其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。
接下来 \(m\) 行每行包含 \(3\) 或 \(4\) 个整数,表示一个操作,具体如下:
1 x y k:将区间 \([x, y]\) 内每个数加上 \(k\)。2 x y:输出区间 \([x, y]\) 内每个数的和。
输出格式
输出包含若干行整数,即为所有操作 2 的结果。
输入输出样例 #1
输入 #1
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
输出 #1
11
8
20
说明/提示
对于 \(15\%\) 的数据:\(n \le 8\),\(m \le 10\)。
对于 \(35\%\) 的数据:\(n \le {10}^3\),\(m \le {10}^4\)。
对于 \(100\%\) 的数据:\(1 \le n, m \le {10}^5\),\(a_i,k\) 为正数,且任意时刻数列的和不超过 \(2\times 10^{18}\)。
【样例解释】
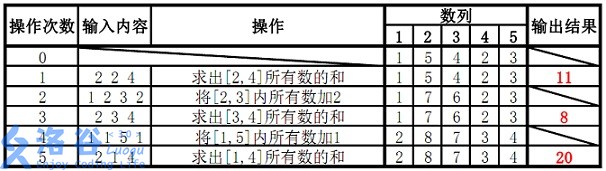
解法&&个人感想
首先,我们从上题的解法得出,区间增加可以用差分的方法得出来
然后,我们用数学公式推导一下区间查询在差分情况下的公式
\(\sum_{i=1}^{n}a[i]=\sum_{i=1}^{n}\sum_{j=1}^{i}b[j]=\sum_{i=1}^{n}(n+1-i)b[i]=(n+1)\sum_{i=1}^{n}b[i]-\sum_{i=1}^{n}i*b[i]\)
于是,我们就能通过维护\(b[i]=a[i]-a[i-1],c[i]=i*b[i]\)两个树状数组,来完成区间查询的工作
那么,区间查找呢?\(b[i]\)的在上题中已经提过,知乎上博主讲的\(c[i]\)的角度比较绕,我从另一个角度讲吧
\(c[i]=i*b[i]=i*(a[i]-a[i-1])\)
那么,还是只需要做两次单点增加,分别是在\(i=x,c[i]+=x*k\)和\(i=y+1,c[i]-=(y+1)*k\)
然后就完成啦,注意:十年OI一场空,不开ll见祖宗
这题的数据范围全开ll也没关系
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 100005
using namespace std;
ll n,m,op,x,y,k;
ll tree[maxn];
ll tree_2[maxn];
ll a[maxn];
ll b[maxn];
ll c[maxn];
ll query(ll x){
ll ans=0;
for(;x;x-=lowbit(x)) ans+=tree[x];
return ans;
}
ll query_2(ll x){
ll ans=0;
for(;x;x-=lowbit(x)) ans+=tree_2[x];
return ans;
}
void update(ll x,ll k){
for(;x<=n;x+=lowbit(x)) tree[x]+=k;
return ;
}
void update_2(ll x,ll k){
for(;x<=n;x+=lowbit(x)) tree_2[x]+=k;
return ;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i]-a[i-1];
c[i]=i*b[i];
update(i,b[i]);
update_2(i,c[i]);
}
for(int i=1;i<=m;i++){
cin>>op;
if(op==1){
cin>>x>>y>>k;
update(x,k);
update(y+1,-k);
update_2(x,x*k);
update_2(y+1,-(y+1)*k);
}
else{
cin>>x>>y;
ll ans_1=(y+1)*query(y)-x*query(x-1);
ll ans_2=query_2(y)-query_2(x-1);
cout<<ans_1-ans_2<<endl;
}
}
system("pause");
return 0;
}
接着,是树状数组在逆序对中的应用
这部分只有一个点不大好理解,我们通过一道例题讲一下
P1908 逆序对
题目描述
猫猫 TOM 和小老鼠 JERRY 最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。
最近,TOM 老猫查阅到一个人类称之为“逆序对”的东西,这东西是这样定义的:对于给定的一段正整数序列,逆序对就是序列中 \(a_i>a_j\) 且 \(i<j\) 的有序对。知道这概念后,他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。注意序列中可能有重复数字。
Update:数据已加强。
输入格式
第一行,一个数 \(n\),表示序列中有 \(n\) 个数。
第二行 \(n\) 个数,表示给定的序列。序列中每个数字不超过 \(10^9\)。
输出格式
输出序列中逆序对的数目。
输入输出样例 #1
输入 #1
6
5 4 2 6 3 1
输出 #1
11
说明/提示
对于 \(25\%\) 的数据,\(n \leq 2500\)。
对于 \(50\%\) 的数据,\(n \leq 4 \times 10^4\)。
对于所有数据,\(1 \leq n \leq 5 \times 10^5\)。
请使用较快的输入输出。
应该不会有人 \(O(n^2)\) 过 50 万吧 —— 2018.8 chen_zhe。
解法&&个人感想
这道题其实也是板子题,说实话
毕竟我们这篇讲的就是板子啊
好了,为什么树状数组可以求逆序对?
因为它对前缀的某个元素有包容性,好了这是我瞎扯的
不过还是可以维护就是了
首先我们明确一下原理,一个逆序对的产生,源自前面的那个数比后面的数大
所以,其实这是一个定性而非定量的研究
那么,我们可以采用离散化
只需要维护一个树状数组\(tree[x]\),其中x元素是原数组\(a[x]\)的输入顺序
代表的数值是这个顺序所代表的原数组的值在原数组中的大小顺序
这样,我们能保证,在update rank[i](i是原数组的输入顺序 rank是大小顺序)被遍历的时候,首先被维护的就是输入顺序
此时,如果在查询query(rank[i])的时候,如果存在比rank[i]大,又比其早输入进的数,那么,这构成一个逆序对
我们看代码:
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 500010
using namespace std;
struct node{
int num,val;
bool operator<(node b){
if(val==b.val) return num<b.num;
return val<b.val;
}
};
node a[maxn];
int tree[maxn],rak[maxn],n;//rank[i]表示第i个数在序列中的排名,如果有比i先加进去的数,排名却在rank[i]后的,说明构成了逆序对
int ans=0;
int query(int x){
int ans=0;
for(;x;x-=lowbit(x)) ans+=tree[x];
return ans;
}
void update(int x,int k){
for(;x<=n;x+=lowbit(x)) tree[x]+=k;
return ;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i].val;
a[i].num=i;
}
sort(a+1,a+1+n);
for(int i=1;i<=n;i++){
rak[a[i].num]=i;
}
for(int i=1;i<=n;i++){
update(rak[i],1);
ans+=i-query(rak[i]);
}
cout<<ans<<endl;
system("pause");
return 0;
}
2025.05.14补充
这次,我们来讲一下用树状数组维护非连续更新值的做法
什么是非连续更新值?就是,这个取值可能某种程度上不受所有值的影响
比如,我们这里讲的就是min和max
下面直接看题:
P2880 [USACO07JAN] Balanced Lineup G
题目描述
For the daily milking, Farmer John's N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. To keep things simple, he will take a contiguous range of cows from the milking lineup to play the game. However, for all the cows to have fun they should not differ too much in height.
Farmer John has made a list of Q (1 ≤ Q ≤ 180,000) potential groups of cows and their heights (1 ≤ height ≤ 1,000,000). For each group, he wants your help to determine the difference in height between the shortest and the tallest cow in the group.
每天,农夫 John 的 \(n(1\le n\le 5\times 10^4)\) 头牛总是按同一序列排队。
有一天, John 决定让一些牛们玩一场飞盘比赛。他准备找一群在队列中位置连续的牛来进行比赛。但是为了避免水平悬殊,牛的身高不应该相差太大。John 准备了 \(q(1\le q\le 1.8\times10^5)\) 个可能的牛的选择和所有牛的身高 \(h_i(1\le h_i\le 10^6,1\le i\le n)\)。他想知道每一组里面最高和最低的牛的身高差。
输入格式
Line 1: Two space-separated integers, N and Q.
Lines 2..N+1: Line i+1 contains a single integer that is the height of cow i
Lines N+2..N+Q+1: Two integers A and B (1 ≤ A ≤ B ≤ N), representing the range of cows from A to B inclusive.
第一行两个数 \(n,q\)。
接下来 \(n\) 行,每行一个数 \(h_i\)。
再接下来 \(q\) 行,每行两个整数 \(a\) 和 \(b\),表示询问第 \(a\) 头牛到第 \(b\) 头牛里的最高和最低的牛的身高差。
输出格式
Lines 1..Q: Each line contains a single integer that is a response to a reply and indicates the difference in height between the tallest and shortest cow in the range.
输出共 \(q\) 行,对于每一组询问,输出每一组中最高和最低的牛的身高差。
输入输出样例 #1
输入 #1
6 3
1
7
3
4
2
5
1 5
4 6
2 2
输出 #1
6
3
0
解法&&个人感想
我们这题,肯定要维护最大和最小两个树状数组的吧
而单点修改其实挺容易想到
问题在于区间查找
经过洛谷某位大佬的指点,我懂得了
我们考虑\(y-lowbit(y)\)与x的关系
如果\(y-lowbit(y)>x\) 那么可以将\([x,y]\)分成两部分,即\([x,y-lowbit(y)]\)和\([y-lowbit(y)+1,y]\),很容易看出后者就是\(tree[y]\)
如果\(y-lowbit(y) \le x\),那么我们考虑将y进行变化,抽出\(a[y]\),将原来的区间变为\([x,y-1]和ma[y]\)两个区间,递归求解
当然,递归的返回条件就是\(x=y\),此时只需要返回当前的初值就行
下面看代码:
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define lowbit(x) (x&(-x))
#define maxn 100005
using namespace std;
int n;
int matree[maxn];
int mitree[maxn];
int ma[maxn];
int x;
int q;
int a,b;
void update(int x,int k){
for(;x<=n;x+=lowbit(x)){
matree[x]=max(matree[x],k);
mitree[x]=min(mitree[x],k);
}
}
int minquery(int x,int y){
if(y==x) return ma[x];
if(y-lowbit(y)>x) return min(mitree[y],minquery(x,y-lowbit(y)));
else return min(ma[y],minquery(x,y-1));
}
int maxquery(int x,int y){
if(x==y) return ma[x];
if(y-lowbit(y)>x) return max(matree[y],maxquery(x,y-lowbit(y)));
else return max(ma[y],maxquery(x,y-1));
}
int main(){
memset(mitree,0x3f,sizeof(mitree));
cin>>n>>q;
for(int i=1;i<=n;i++){
cin>>ma[i];
update(i,ma[i]);
}
for(int i=1;i<=q;i++){
cin>>a>>b;
int ans_1=minquery(a,b);
int ans_2=maxquery(a,b);
cout<<ans_2-ans_1<<endl;
}
system("pause");
return 0;
}
后半学期,也请各位继续关注:
《我的青春线代物语果然有问题》
《高数女主养成计划》
《程设の旅》
《青春猪头少年不会梦到多智能体吃豆人》
《某Linux的开源软件》
还有——
《我的算法竞赛不可能这么可爱》
本期到此结束!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号