【洛谷P1991 P2872 P1265】几道生成树的抖机灵题目
早上并行操作的时候加训了几道
三道题 两黄一绿 想到了就不是难题
先看第一道:
P1991 无线通讯网
题目描述
国防部计划用无线网络连接若干个边防哨所。2 种不同的通讯技术用来搭建无线网络;
每个边防哨所都要配备无线电收发器;有一些哨所还可以增配卫星电话。
任意两个配备了一条卫星电话线路的哨所(两边都有卫星电话)均可以通话,无论他们相距多远。而只通过无线电收发器通话的哨所之间的距离不能超过 \(D\),这是受收发器的功率限制。收发器的功率越高,通话距离 \(D\) 会更远,但同时价格也会更贵。
收发器需要统一购买和安装,所以全部哨所只能选择安装一种型号的收发器。换句话说,每一对哨所之间的通话距离都是同一个 \(D\)。你的任务是确定收发器必须的最小通话距离 \(D\),使得每一对哨所之间至少有一条通话路径(直接的或者间接的)。
输入格式
第一行,\(2\) 个整数 \(S\) 和 \(P\),\(S\) 表示可安装的卫星电话的哨所数,\(P\) 表示边防哨所的数量。
接下里 \(P\) 行,每行两个整数 \(x,y\) 描述一个哨所的平面坐标 \((x, y)\),以 km 为单位。
输出格式
第一行,\(1\) 个实数 \(D\),表示无线电收发器的最小传输距离,精确到小数点后两位。
输入输出样例 #1
输入 #1
2 4
0 100
0 300
0 600
150 750
输出 #1
212.13
说明/提示
数据范围及约定
- 对于 \(20\%\) 的数据:\(P = 2,S = 1\);
- 对于另外 \(20\%\) 的数据:\(P = 4,S = 2\);
- 对于 \(100\%\) 的数据保证:\(1 ≤ S ≤ 100\),\(S < P ≤ 500\),\(0 ≤ x,y ≤ 10000\)。
解法&&个人感想
题目可能有点难理解 但是大概意思说 所有卫星电话无视距离可以直接通话
所以 最终状态是题目中有S个联通块
而后面的“每一对哨所之间至少有一条通话路径” 明显是最小生成树了吧?
这里肯定用Kruscal的
下面看代码:
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define maxm 500001
#define maxn 505
using namespace std;
struct Edge{
int from,to;
float w;
};
Edge edge[maxm];
int s,p;
int x[maxn],y[maxn];
int fa[maxn];
int cnt,tot;
double ans=0;
bool cmp(Edge x,Edge y){
return x.w<y.w;
}
int get(int x){
if(fa[x]==x) return x;
return fa[x]=get(fa[x]);
}
void merge(int x,int y){
fa[x]=y;
}
int main(){
scanf("%d%d",&s,&p);
for(int i=1;i<=p;i++){
scanf("%d%d",&x[i],&y[i]);
}
for(int i=1;i<=p;i++) fa[i]=i;
for(int i=1;i<=p;i++){
for(int j=i+1;j<=p;j++){
edge[++cnt].from=i;
edge[cnt].to=j;
edge[cnt].w=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));
}
}
sort(edge+1,edge+1+cnt,cmp);
for(int i=1;i<=cnt;i++){
int x=get(edge[i].from),y=get(edge[i].to);
if(x==y) continue;
merge(x,y);
ans=edge[i].w;
tot++;
if(tot==p-s){
break;
}
}
printf("%.2lf",ans);
system("pause");
return 0;
}
下面看第二题:
P2872 [USACO07DEC] Building Roads S
题目描述
Farmer John had just acquired several new farms! He wants to connect the farms with roads so that he can travel from any farm to any other farm via a sequence of roads; roads already connect some of the farms.
Each of the N (1 ≤ N ≤ 1,000) farms (conveniently numbered 1..N) is represented by a position (Xi, Yi) on the plane (0 ≤ Xi ≤ 1,000,000; 0 ≤ Yi ≤ 1,000,000). Given the preexisting M roads (1 ≤ M ≤ 1,000) as pairs of connected farms, help Farmer John determine the smallest length of additional roads he must build to connect all his farms.
给定 \(n\) 个点的坐标,第 \(i\) 个点的坐标为 \((x_i,y_i)\),这 \(n\) 个点编号为 \(1\) 到 \(n\)。给定 \(m\) 条边,第 \(i\) 条边连接第 \(u_i\) 个点和第 \(v_i\) 个点。现在要求你添加一些边,并且能使得任意一点都可以连通其他所有点。求添加的边的总长度的最小值。
输入格式
* Line 1: Two space-separated integers: N and M
* Lines 2..N+1: Two space-separated integers: Xi and Yi
* Lines N+2..N+M+2: Two space-separated integers: i and j, indicating that there is already a road connecting the farm i and farm j.
第一行两个整数 \(n,m\) 代表点数与边数。
接下来 \(n\) 行每行两个整数 \(x_i,y_i\) 代表第 \(i\) 个点的坐标。
接下来 \(m\) 行每行两个整数 \(u_i,v_i\) 代表第 \(i\) 条边连接第 \(u_i\) 个点和第 \(v_i\) 个点。
输出格式
* Line 1: Smallest length of additional roads required to connect all farms, printed without rounding to two decimal places. Be sure to calculate distances as 64-bit floating point numbers.
一行一个实数代表添加的边的最小长度,要求保留两位小数,为了避免误差, 请用 \(64\) 位实型变量进行计算。
输入输出样例 #1
输入 #1
4 1
1 1
3 1
2 3
4 3
1 4
输出 #1
4.00
说明/提示
数据规模与约定
对于 \(100\%\) 的整数,\(1 \le n,m \le 1000\),\(1 \le x_i,y_i \le 10^6\),\(1 \le u_i,v_i \le n\)。
说明
Translated by 一只书虫仔。
解法&&个人感想
这道题的关键在于“已经修好的路”要怎么处理
我一开始的想法是在Edge结构体里加一个判断变量
但是,这样边权不会改变 如果存在很多更小的边的话,就会导致那些边被优先选择
这样是不行的
所以 我们要将已经赋值的边 赋值为0
保证其被优先选择
下面看代码:
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define maxn 5005
#define maxm 500005
using namespace std;
int n,m;
int x[maxn],y[maxn];
struct Edge{
int from,to,pd;
double w;
};
Edge edge[maxm];
int fa[maxn];
int cnt=0;
int u,v;
double ans=0;
int k=0;
bool cmp(Edge x,Edge y){
return x.w<y.w;
}
int get(int x){
if(fa[x]==x) return x;
return fa[x]=get(fa[x]);
}
void merge(int x,int y){
fa[x]=y;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d%d",&x[i],&y[i]);
}
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
edge[++cnt].from=i;
edge[cnt].to=j;
edge[cnt].w=sqrt((ll)(x[i]-x[j])*(ll)(x[i]-x[j])+(ll)(y[i]-y[j])*(ll)(y[i]-y[j]));
}
}
for(int i=1;i<=m;i++){
scanf("%d%d",&u,&v);
int mi=min(u,v),ma=max(u,v);
for(int j=1;j<=cnt;j++){
if(mi==edge[j].from&&ma==edge[j].to){
edge[j].w=0;
break;
}
}
}
sort(edge+1,edge+1+cnt,cmp);
for(int i=1;i<=cnt;i++){
int x=get(edge[i].from),y=get(edge[i].to);
if(x==y) continue;
merge(x,y);
ans+=edge[i].w;
}
printf("%.2lf",ans);
system("pause");
return 0;
}
下面看第三道题:
P1265 公路修建
题目描述
某国有 \(n\) 个城市,它们互相之间没有公路相通,因此交通十分不便。为解决这一“行路难”的问题,政府决定修建公路。修建公路的任务由各城市共同完成。
修建工程分若干轮完成。在每一轮中,每个城市选择一个与它最近的城市,申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。
政府审批的规则如下:
- 如果两个或以上城市申请修建同一条公路,则让它们共同修建;
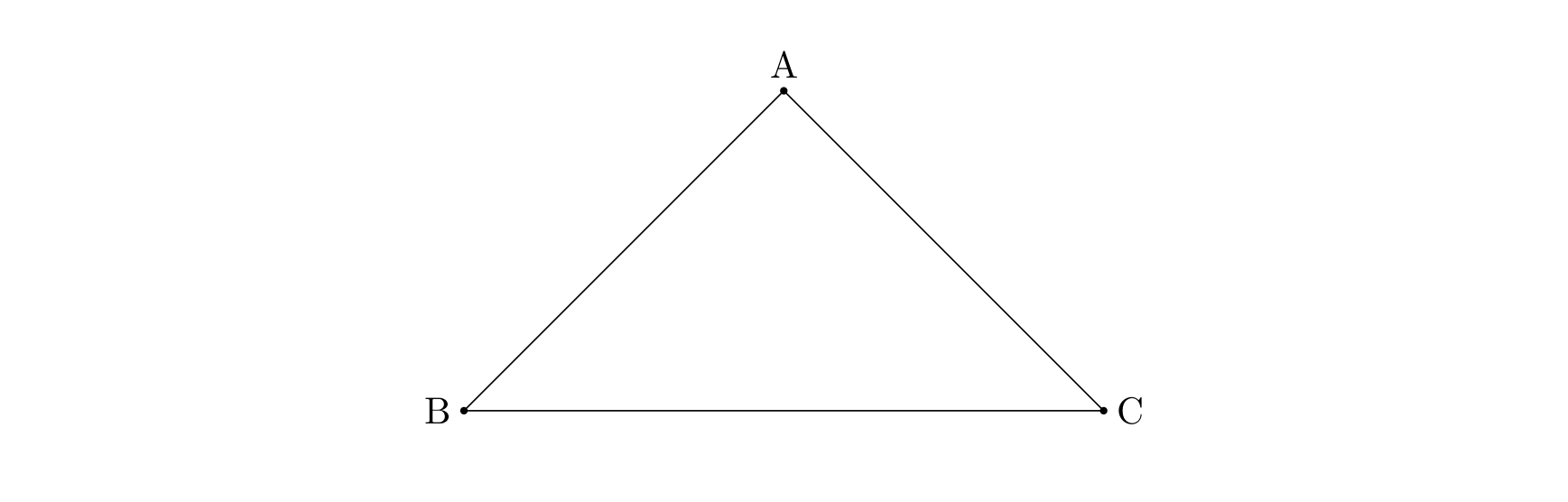
- 如果三个或以上的城市申请修建的公路成环。如下图,A 申请修建公路 AB,B 申请修建公路 BC,C 申请修建公路 CA。则政府将否决其中最短的一条公路的修建申请;
- 其他情况的申请一律同意。
一轮修建结束后,可能会有若干城市可以通过公路直接或间接相连。这些可以互相连通的城市即组成“城市联盟”。在下一轮修建中,每个“城市联盟”将被看作一个城市,发挥一个城市的作用。
当所有城市被组合成一个“城市联盟”时,修建工程也就完成了。
你的任务是根据城市的分布和前面讲到的规则,计算出将要修建的公路总长度。
输入格式
第一行一个整数 \(n\),表示城市的数量。(\(n \leq 5000\))
以下 \(n\) 行,每行两个整数 \(x\) 和 \(y\),表示一个城市的坐标。(\(-10^6 \leq x,y \leq 10^6\))
输出格式
一个实数,四舍五入保留两位小数,表示公路总长。(保证有唯一解)
输入输出样例 #1
输入 #1
4
0 0
1 2
-1 2
0 4
输出 #1
6.47
说明/提示
修建的公路如图所示:
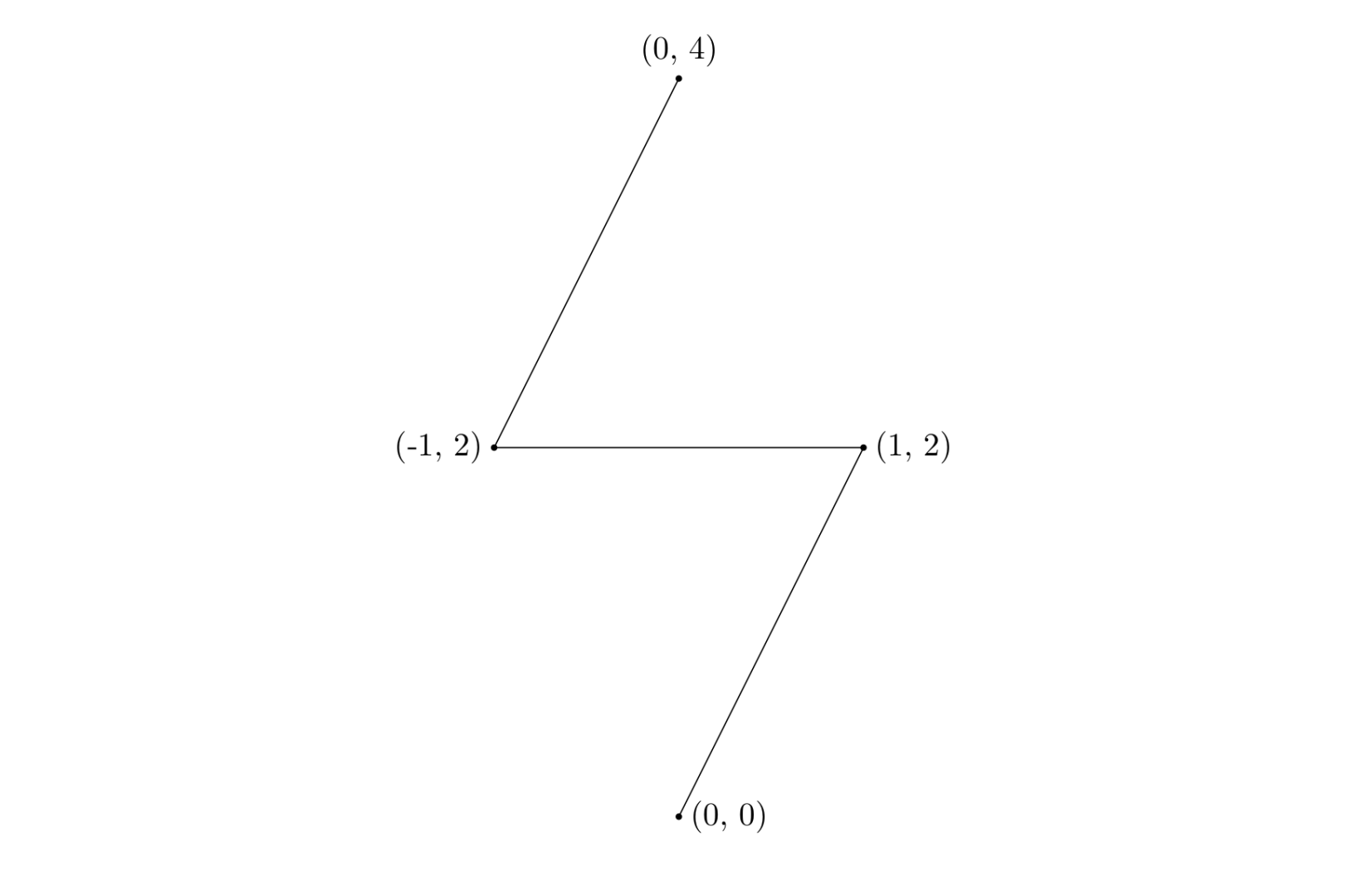
解法&&个人感想
我一开始就觉得这个条件二怪怪的 你删掉一条边 并不影响它们的连通性
然后就按照正常思路做了
后面看题解才发现 我测 这个条件压根不成立 搞屁啊
虽然最后结果是一样的就是了
但是这题有几个需要注意的点:
1.$ 10^6 \(的范围平方会爆int 需要强制转ll
2.这题m比较大 所以不能用heap-prim或者前向星的prim
要用最暴力的O(\) n^2 $)的prim
这很坑
下面看代码:
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define maxn 5005
#define maxm 50000005
using namespace std;
int n,tot;
int x[maxn],y[maxn];
double d[maxn];
int vis[maxn];
double ans=0;
double query(int i,int j){
return sqrt((ll)(x[i]-x[j])*(ll)(x[i]-x[j])+(ll)(y[i]-y[j])*(ll)(y[i]-y[j]));
}
void prim(){
for(int i=0;i<=n;i++) d[i]=1e8*1.0;
d[1]=0.0;
for(int i=1;i<=n;i++){
int x=0;
for(int j=1;j<=n;j++){
if(!vis[j]&&d[j]<d[x]) x=j;
}
vis[x]=1;
for(int y=1;y<=n;y++){
if(!vis[y]&&d[y]>query(x,y)){
d[y]=query(x,y);
}
}
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d",&x[i],&y[i]);
}
prim();
for(int i=1;i<=n;i++) ans+=d[i];
printf("%.2lf",ans);
system("pause");
return 0;
}
放图




 浙公网安备 33010602011771号
浙公网安备 33010602011771号