【洛谷P2419&&洛谷P2047】Cow Contest S&&社交网络[NOI2007]
今天做了两道题
话说为啥这两道题都是Floyd的变式
变式就变式吧 反正有点思考量
先看第一道
P2419 [USACO08JAN] Cow Contest S
题目描述
$ N (1 ≤ N ≤ 100) $ cows, conveniently numbered $ 1 ~ N $ , are participating in a programming contest. As we all know, some cows code better than others. Each cow has a certain constant skill rating that is unique among the competitors.
The contest is conducted in several head-to-head rounds, each between two cows. If cow $ A $ has a greater skill level than cow $ B (1 ≤ A ≤ N; 1 ≤ B ≤ N; A ≠ B) $, then cow $ A $ will always beat cow $ B $ .
Farmer John is trying to rank the cows by skill level. Given a list the results of $ M (1 ≤ M ≤ 4,500) $ two-cow rounds, determine the number of cows whose ranks can be precisely determined from the results. It is guaranteed that the results of the rounds will not be contradictory.
FJ的 \(N\)(\(1 \leq N \leq 100\))头奶牛们最近参加了场程序设计竞赛。在赛场上,奶牛们按 \(1, 2, \cdots, N\) 依次编号。每头奶牛的编程能力不尽相同,并且没有哪两头奶牛的水平不相上下,也就是说,奶牛们的编程能力有明确的排名。 整个比赛被分成了若干轮,每一轮是两头指定编号的奶牛的对决。如果编号为 \(A\) 的奶牛的编程能力强于编号为 \(B\) 的奶牛 (\(1 \leq A, B \leq N\),\(A \neq B\)),那么她们的对决中,编号为 \(A\) 的奶牛总是能胜出。 FJ 想知道奶牛们编程能力的具体排名,于是他找来了奶牛们所有 \(M\)(\(1 \leq M \leq 4,500\))轮比赛的结果,希望你能根据这些信息,推断出尽可能多的奶牛的编程能力排名。比赛结果保证不会自相矛盾。
输入格式
第一行两个用空格隔开的整数 \(N, M\)。
第 \(2\sim M + 1\) 行,每行为两个用空格隔开的整数 \(A, B\) ,描述了参加某一轮比赛的奶牛的编号,以及结果(每行的第一个数的奶牛为胜者)。
输出格式
输出一行一个整数,表示排名可以确定的奶牛的数目。
输入输出样例 #1
输入 #1
5 5
4 3
4 2
3 2
1 2
2 5
输出 #1
2
说明/提示
样例解释:
编号为 \(2\) 的奶牛输给了编号为 \(1, 3, 4\) 的奶牛,也就是说她的水平比这 \(3\) 头奶牛都差。而编号为 \(5\) 的奶牛又输在了她的手下,也就是说,她的水平比编号为 \(5\) 的奶牛强一些。于是,编号为 \(2\) 的奶牛的排名必然为第 \(4\),编号为 \(5\) 的奶牛的水平必然最差。其他 \(3\) 头奶牛的排名仍无法确定。
解法&&个人感想
这题画图就知道 满足条件的Cow 一定能够直接或者间接到达其他所有的cow
然后 Floyd 判断连通性 也就是传递闭包 这个应该都会吧?
直接看代码:
#include<bits/stdc++.h>
#define maxn 105
#define maxm 4005
#define ll long long
using namespace std;
int n,m;
int x,y,z;
bool ma[maxn][maxn];
int ans=0;
int l=0,r=n-1;
int res[maxn];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
ma[i][j]=false;
}
}
for(int i=1;i<=n;i++) ma[i][i]=true;
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
ma[y][x]=true;
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
ma[i][j]=ma[i][j]|(ma[i][k]&ma[k][j]);
}
}
}
for(int i=1;i<=n;i++){
int flag=0;
for(int j=1;j<=n;j++){
if(ma[i][j]||ma[j][i]) flag++;
}
if(flag==n) ans++;
}
printf("%d",ans);
system("pause");
return 0;
}
然后是第二道:
P2047 [NOI2007] 社交网络
题目描述
在社交网络 ( Social Network ) 的研究中,我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题:
在一个社交圈子里有 \(n\) 个人,人与人之间有不同程度的关系。我们将这个关系网络对应到一个 \(n\) 个结点的无向图上,两个不同的人若互相认识,则在他们对应的结点之间连接一条无向边,并附上一个正数权值 \(c\) ,\(c\) 越小,表示两个人之间的关系越密切。我们可以用对应结点之间的最短路长度来衡量两个人 \(s\) 和 \(t\) 之间的关系密切程度,注意到最短路径上的其他结点为 \(s\) 和 \(t\) 的联系提供了某种便利,即这些结点对于 \(s\) 和 \(t\) 之间的联系有一定的重要程度。我们可以通过统计经过一个结点 \(v\) 的最短路径的数目来衡量该结点在社交网络中的重要程度。考虑到两个结点 \(A\) 和 \(B\) 之间可能会有多条最短路径。我们修改重要程度的定义如下:令 \(C_{s,t}\) 表示从s到t的不同的最短路的数目,\(C_{s,t}(v)\) 表示经过 \(v\) 从 \(s\) 到 \(t\) 的最短路的数目;则定义:
为结点 \(v\) 在社交网络中的重要程度。为了使 \(I(v)\) 和 \(C_{s,t}(v)\) 有意义,我们规定需要处理的社交网络都是连通的无向图,即任意两个结点之间都有一条有限长度的最短路径。现在给出这样一幅描述社交网络的加权无向图,请你求出每一个结点的重要程度。
输入格式
输入第一行有两个整数 \(n\) 和 \(m\) ,表示社交网络中结点和无向边的数目。
在无向图中,我们将所有结点从 \(1\) 到 \(n\) 进行编号。
接下来 \(m\) 行,每行用三个整数 \(a , b , c\) 描述一条连接结点 \(a\) 和 \(b\) ,权值为 \(c\) 的无向边。
注意任意两个结点之间最多有一条无向边相连,无向图中也不会出现自环(即不存在一条无向边的两个端点是相同的结点)。
输出格式
输出包括 \(n\) 行,每行一个实数,精确到小数点后 \(3\) 位。第 \(i\) 行的实数表示结点 \(i\) 在社交网络中的重要程度。
输入输出样例 #1
输入 #1
4 4
1 2 1
2 3 1
3 4 1
4 1 1
输出 #1
1.000
1.000
1.000
1.000
说明/提示
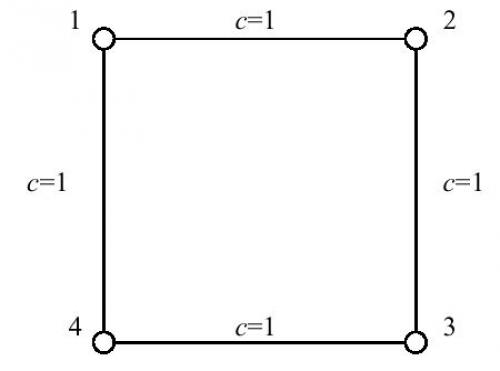
对于1号结点而言,只有2号到4号结点和4号到2号结点的最短路经过1号结点,而2号结点和4号结点之间的最短路又有2条。因而根据定义,1号结点的重要程度计算为1/2+1/2=1。由于图的对称性,其他三个结点的重要程度也都是1。
对于 \(50\%\) 的数据, \(n \le 10 , m \le 45\)。
对于 \(100\%\) 的数据, \(n \le 100 , m \le 4500\) ,任意一条边的权值 \(c\) 是正整数且 \(1 \leqslant c \leqslant 1000\) 。
所有数据中保证给出的无向图连通,且任意两个结点之间的最短路径数目不超过 \(10^{10}\)。
解法&&个人感想
我们之前做过了那道“最短路计数”对吧?其实这题的思路差不多
一看到经过v的s、t间最短路 我就想到用ma[s][t]=ma[s][v]=ma[v][k]以及cnt[s][t]=cnt[s][v]*cnt[v][r]更新
然后就完了
一开始脑子有点神金 cnt[x][y]不知道赋多少初值 后面想想你对每条连的边赋成1不就行了?
还有 警示后人 开float不开double会WA 70pts
下面看代码:
#include<bits/stdc++.h>
#define maxn 105
#define maxm 4505
#define ll long long
using namespace std;
ll ma[maxn][maxn];
ll cnt[maxn][maxn];
double ans[maxn];
int n,m,x,y,z;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
ma[i][j]=1e8;
}
}
for(int i=1;i<=n;i++) ma[i][i]=0;
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
ma[x][y]=z;
ma[y][x]=z;
cnt[x][y]=1;
cnt[y][x]=1;
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(ma[i][j]>ma[i][k]+ma[k][j]){
cnt[i][j]=cnt[i][k]*cnt[k][j];
ma[i][j]=ma[i][k]+ma[k][j];
}
else if(ma[i][j]==ma[i][k]+ma[k][j]){
cnt[i][j]+=cnt[i][k]*cnt[k][j];
}
}
}
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==k||k==j||i==j) continue;
if(ma[i][k]+ma[k][j]==ma[i][j]){
ans[k]+=(1.0*cnt[i][k]*cnt[k][j])/cnt[i][j];
}
}
}
}
for(int i=1;i<=n;i++){
printf("%.3lf\n",ans[i]);
}
system("pause");
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号