【洛谷SP1805】最大矩形面积

今天开始学一点数据结构

（右下角小火箭可以回到页首）
大家应该都能看出来这题应该用的是单调栈
我们先来看看单调栈的模版

P5788 【模板】单调栈

题目背景

模板题，无背景。

2019.12.12 更新数据，放宽时限，现在不再卡常了。

题目描述

给出项数为 \(n\) 的整数数列 \(a_{1 \dots n}\)。

定义函数 \(f(i)\) 代表数列中第 \(i\) 个元素之后第一个大于 \(a_i\) 的元素的下标，即 \(f(i)=\min_{i<j\leq n, a_j > a_i} \{j\}\)。若不存在，则 \(f(i)=0\)。

试求出 \(f(1\dots n)\)。

输入格式

第一行一个正整数 \(n\)。

第二行 \(n\) 个正整数 \(a_{1\dots n}\)。

输出格式

一行 \(n\) 个整数表示 \(f(1), f(2), \dots, f(n)\) 的值。

输入输出样例 #1

输入 #1

5
1 4 2 3 5

输出 #1

2 5 4 5 0

说明/提示

【数据规模与约定】

对于 \(30\%\) 的数据，\(n\leq 100\)；

对于 \(60\%\) 的数据，\(n\leq 5 \times 10^3\) ；

对于 \(100\%\) 的数据，\(1 \le n\leq 3\times 10^6\)，\(1\leq a_i\leq 10^9\)。

解法

看数据范围可以得知 这道题一定要用O(n)的算法
单调栈 顾名思义 就是维护一个具有单调性质的栈
那么当碰到栈顶和准备入栈的元素不满足单调性质时怎么办呢？
答案是不断出栈知道满足单调性
没错 这就是单调栈的基本思路

#include<bits/stdc++.h>
using namespace std;
int n;
int a[3000005],f[3000005];
stack<int>s;
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
    }
    for(int i=n;i>=1;i--){
        while(!s.empty()&&a[i]>=a[s.top()]) s.pop();
        if(s.empty()) f[i]=0;
        else f[i]=s.top();
        s.push(i);
    }
    for(int i=1;i<=n;i++){
        cout<<f[i]<<' ';
    }
    system("pause");
    return 0;
}

　　

然后我们再来看这道矩形面积的题目
为什么这道题能有绿题的难度？自然有它的道理
下面是题面

SP1805 HISTOGRA - Largest Rectangle in a Histogram

题目描述

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

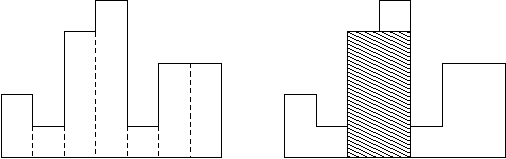Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

输入格式

无

输出格式

无

输入输出样例 #1

输入 #1

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出 #1

8
4000

显而易见本题也是O(n)算法
好的 我们考虑极端情况
是不是当所有元素都单调的时候 我们通过比较一个ans（代表该格子与右侧格子的距离）
就能够完成了呢？
好的 那么考虑不满足单调的情况
如果不满足单调的话 那么此时前面比要入栈元素高的部分就没用了
因此逐一出栈并与ans比较 然后再把这几个合并一下重新入栈（这里比较难想）
就可以啦
不过 有STL就不要手搓栈了哦~

#include<bits/stdc++.h>
#define ll long long
using namespace std;
struct node{
    ll h,w;
};
ll h[100005];
int p;
int n;
ll ans;
int main(){
    while(cin>>n&&n){
        memset(h,0,sizeof(h));
        ans=0;
        for(int i=1;i<=n;i++){
            scanf("%lld",&h[i]);
        }
        h[n+1]=0;
        stack<node>s;
        for(int i=1;i<=n+1;i++){//加一个n+1防止扫描到最后还有矩形
            ll wi=0;
            while(!s.empty()&&h[i]<s.top().h){
                wi+=s.top().w;
                ans=max(ans,wi*s.top().h);
                s.pop();
            }
            s.push(node{h[i],wi+1});
        }
        printf("%lld\n",ans);//ll的时候用printf一定要注意啊
    }
    system("pause");
    return 0;
}

　　

本期完结撒花！