Burnside/Pólya
前几天看OI 中的群论,我才发现我又忘了
唐诗博客↓
Burnside 定理:
Pólya 定理(由上面定理得):
P5233 [JSOI2012] 爱之项链
戒指部分套公式,项链部分用容斥求。枚举有多少个相邻位置冲突。
没写代码
P4128 [SHOI2006] 有色图&双倍经验
私人标题党,害得我点进去看有没有色图。
用 Burnside 定理,但是 \(|G|\) 太大了。我们可以发现对于置换“循环”的大小的集合是一样的话,算出来的方案也是固定的。所以枚举数的分拆(dfs),一个数的分拆,可以想象成把标号分配到几个盒子里,对于 \(x\) 个相同的盒子来说方案就多算了 \(x!\) 次。对于一个盒子内,标号的顺序如果通过右旋变为一样的话就是一个方案,所以说对于一个数的分拆,有 $ \frac{n!}{\prod a!\prod b}$,其中 \(a\) 是对于每一个数,在数的分拆中出现的次数,\(\prod b\) 是数的分拆中拆出来的数的乘积。
先考虑当边的端点都在一个循环内的情况,那边循环的个数为 \(\lfloor \frac{p}{2}\rfloor\)(\(p\) 是这个循环的大小,边 \((0,k)\) 与边 \((1,k+1)\) 在一个边循环内)。
再考虑当边的端点不在一个循环内的情况,那在一个边循环内边的个数相当于边的两个端点不断在循环上跑,最终回到原点要跑的次数,所以是 \([a,b]\)(\(a,b\) 是这两个循环的大小),那产生的边循环数就是 \(\frac{ab}{[a,b]}=(a,b)\) 了。
如图所示(分拆为 \(4,5\) 的情况,循环内部的不同的边循环用不同颜色表示,其他的连线是边的端点不在一个循环内的边循环,而且都在同一个边循环内所以都是红色):
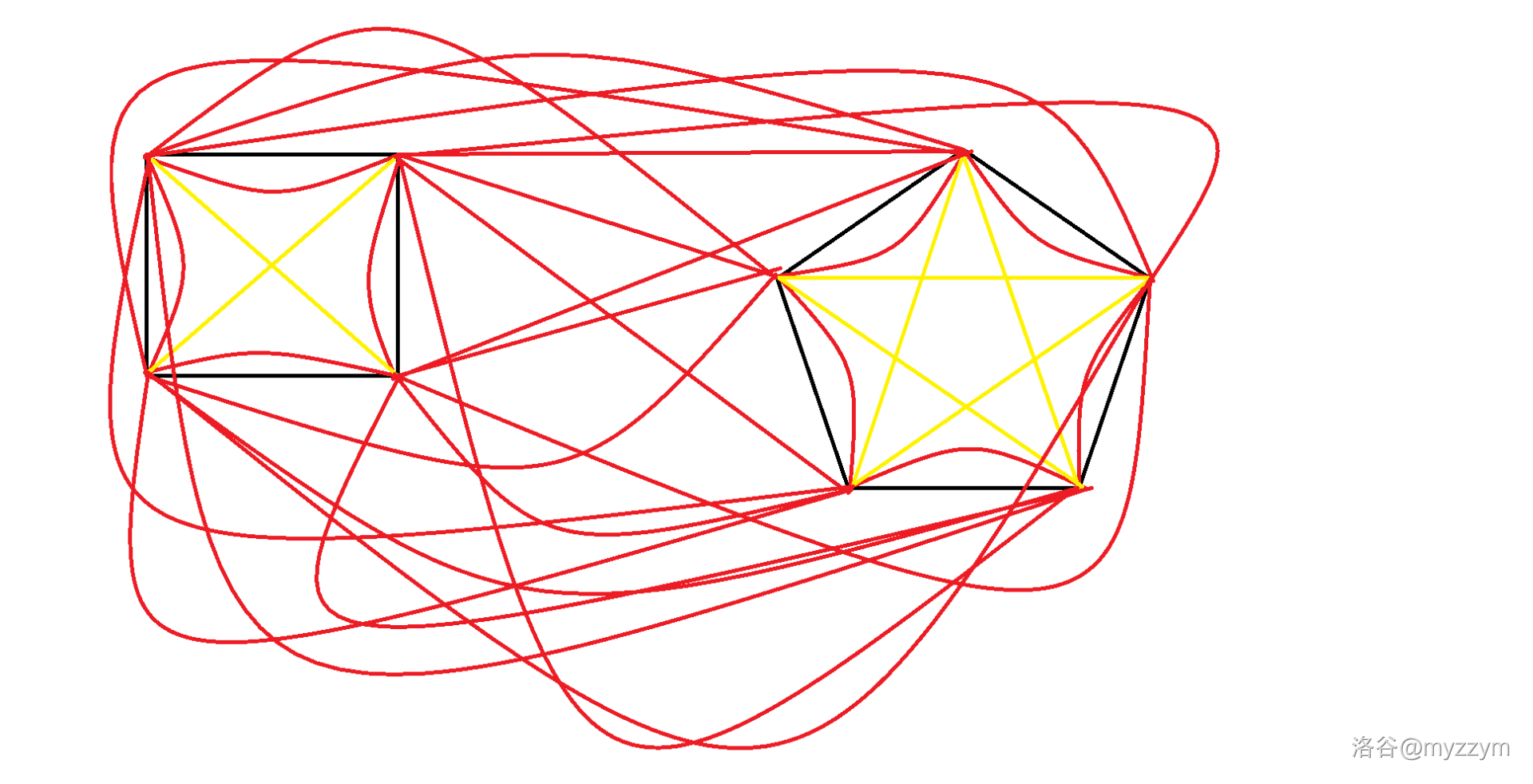
还是太丑了
时间复杂度 \(O(\sum_{p\in n个点的拆分方案集合}|p|^2)\) (gcd预处理,有大蛇去oies上看过这个值大概是三百多万(没看清楚),是不会超时的)
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=100;
int n,m,mod,ans,jc[N],invj[N],inv[N],gd[N][N];
void init(){
jc[0]=jc[1]=invj[0]=invj[1]=inv[0]=inv[1]=1;
for(int i=2;i<=n;i++){
jc[i]=jc[i-1]*i%mod;
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
invj[i]=invj[i-1]*inv[i]%mod;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
gd[i][j]=__gcd(i,j);
}
int Pow(int a,int n){
int ans=1;
while(n){
if(n&1)ans=ans*a%mod;
a=a*a%mod,n>>=1;
}
return ans;
}
vector<int>a;
void dfs(int o,int s){
if(!o){
int sum=1,cnt=0,cnt2=0;
for(int i=0;i<a.size();i++){
sum=sum*inv[a[i]]%mod;
if(i!=0&&a[i]!=a[i-1])sum=sum*invj[cnt2]%mod,cnt2=0;
cnt2++;
cnt+=a[i]/2;
for(int j=0;j<i;j++)
cnt+=gd[a[j]][a[i]];
}
sum=sum*invj[cnt2]%mod;
ans=(ans+sum*Pow(m,cnt))%mod;
return;
}
if(!s)return;
if(o>=s){
a.push_back(s);
dfs(o-s,s);
a.pop_back();
}
dfs(o,s-1);
}
signed main(){
scanf("%lld%lld%lld",&n,&m,&mod);
init();
dfs(n,n);
printf("%lld",ans);
return 0;
}
P4708 画画
可以发现他每次画画都画出来个欧拉回路。
所以题目要求有多少个不同的无标号的图使得每个连通块都是欧拉回路。
转换为每个点度数为偶数。
依旧考虑把边分成端点在不在一个循环内考虑(变量名和上题一样)。当在一个循环内时,当且仅当 \(p\) 为偶数时,都是对角线的边循环染色(说人话就是把这个边循环的边都选择)才会导致这个循环内的所有点度数奇偶变化(自己想一下)。
当不在一个循环内时我们可以算出一个边循环会让每个点连了几条边,a 循环的每个点会连 \(c=[a,b]/a=\frac{b}{(a,b)}\) 条,b 循环的每个点会连 \(d=\frac{a}{(a,b)}\) 条。
分类讨论,当 \(c\) 和 \(d\) 都是偶数的情况:不存在。
当 \(c\) 为奇数,\(d\) 为偶数的情况:选一个这种边循环,能改变 a 的每个点的奇偶性。
当 \(c\) 为偶数,\(d\) 为奇数的情况:同理
当 \(c\) 为奇数,\(d\) 为奇数的情况:选一个这种边循环,能改变 a 和 b 的每个点的奇偶性。
那问题很明显了,我们先把一个循环缩成一个点(可以代表循环内所有点的奇偶性),对于一个点可以选择 x 个边循环使得该点奇偶性变化,称之为可以进行 x 次点操作,还可以选择一些边循环使得两个点奇偶发生变化,我们让这两个点连边,选一条边称之为边操作(可以改变多少次,就连多少条重边)。
设 \(o\) 为一个连通块内所有点可点操作的次数和,\(q\) 为~边~次数和。
我们发现,对于一个连通块内,总点操作次数一定为偶数,因为边操作不会改变连通块内点奇偶性异或和。
我们发现,对每个连通块求出一个生成树,当其他边操作任意做,点操作做偶数次时,这个生成树上的边是否选择是固定的(可以考虑类似于树形dp,叶子节点状态决定边选不选,然后一步一步往上推。因为异或和为 \(0\) 所以保证有解),且不会算漏方案(对于一个合法方案,用分开生成树和非生成树上的边,一样可以求出这个方案)。
在一个连通块内,我们先算点操作的贡献:\(\sum_{i>=0,i<=o,i是偶数}\binom{o}{i}=2^{o-1}\),当 \(o=0\) 时则改为 \(1\)。
再算边操作的贡献:\(2^{q-连通块点数+1}\),就是总边数减去生成树边数。
不要漏掉其他啥也不是的边循环的贡献,再把所有连通块的贡献乘起来,然后一样的就做完了。
把贡献乘在一起后化简一下,其实是和上一题一样,但是每当一个连通块的 \(o>0\) 时,贡献额外除以 \(2\)。
时间复杂度一样,只要用快一点的并查集。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=100,mod=998244353;
int n,ans,jc[N],invj[N],inv[N],gd[N][N],fa[N],gb[N],sm[N];
void init(){
jc[0]=jc[1]=invj[0]=invj[1]=inv[0]=inv[1]=1;
for(int i=2;i<=n;i++){
jc[i]=jc[i-1]*i%mod;
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
invj[i]=invj[i-1]*inv[i]%mod;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
gd[i][j]=__gcd(i,j);
}
int Pow(int a,int n){
int ans=1;
while(n){
if(n&1)ans=ans*a%mod;
a=a*a%mod,n>>=1;
}
return ans;
}
int getfa(int x){return fa[x]==x?x:fa[x]=getfa(fa[x]);}
vector<int>a;
void dfs(int o,int s){
if(!o){
int sum=1,cnt=0,cnt2=0;
for(int i=0;i<a.size();i++){
sum=sum*inv[a[i]]%mod;
fa[i]=i,gb[i]=sm[i]=0;
if(i!=0&&a[i]!=a[i-1])sum=sum*invj[cnt2]%mod,cnt2=0;
cnt2++;
cnt+=a[i]/2;
gb[i]+=a[i]%2==0;
for(int j=0;j<i;j++){
int gc=gd[a[j]][a[i]];
cnt+=gc;
if((a[i]/gc&1)&&(a[j]/gc&1))
fa[getfa(i)]=getfa(j);
else if(a[i]/gc&1)gb[j]++;
else if(a[j]/gc&1)gb[i]++;
}
}
for(int i=0;i<a.size();i++)
sm[getfa(i)]+=gb[i];
for(int i=0;i<a.size();i++)
cnt+=fa[i]==i&&(!sm[i]);
cnt-=a.size();
sum=sum*invj[cnt2]%mod;
ans=(ans+sum*Pow(2,cnt))%mod;
return;
}
if(!s)return;
if(o>=s){
a.push_back(s);
dfs(o-s,s);
a.pop_back();
}
dfs(o,s-1);
}
signed main(){
scanf("%lld",&n);
init();
dfs(n,n);
printf("%lld",ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号