几何就是将现实空间简化成一些简单的元素,那就从认识最基础的元素开始。
元素
从一个点开始,点动成线,线动成面。
元素分为:
- 点
- 线
- 面
线分为:
- 直线
- 曲线
- 切线
- 复合线(多根线组成,相交线、平行线...)
两条线的不同摆放方式,分为:
- 平行
- 相交
线通过旋转的方式,可以生成图形:
- 角(固定一端,移动一端)
- 正方形、长方形(平移)
- 圆形(固定一端,移动一周)
- 复合图形(多个角、正方形、圆形组合而成)
角根据旋转的幅度可以分为:
- 锐角
- 直角
- 钝角
- 平角
从生活经验中抽取出了最简单直观的10条基础,这10条基础无需再解释。
5条公设和5条公理
分为5条最基础的一般性共性,和5条适用于整个平面几何体系的一般性共性:
公理(一般性公理):
-
等同于相同事物的事物会相互等同。
如果a=b,b=c,
那么a=c; -
若等同物加上等同物,则整体会相等。
如果a=b,c=d,
那么a+c=b+d; -
若等同物减去等同物,则其差会相等。
如果a=b,c=d,
那么a-c=b-d; -
相互重合的事物会相互等同。
彼此能重合的物体(图形)是全等的; -
整体大于部分。
公设(也叫几何公理):
-
两点确定一条直线。

-
直线可以无限延长。

-
给定任意线段,可以以其一个端点作为圆心,该线段作为半径作一个圆。
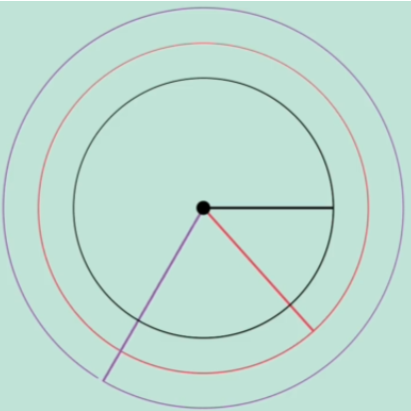
-
所有直角相等。
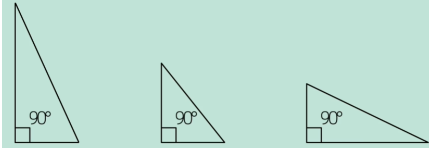
-
若两条直线都与第三条直线相交,并且在同一边的内角之和小于两个直角,则这两条直线在这一边必定相交。
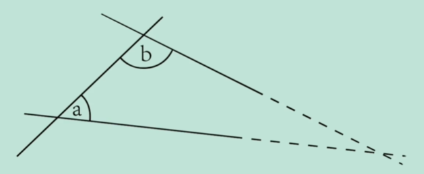
第五公设的解释:
若一条直线与两条直线相交,并且它们在某一侧的内角和小于两个直角(即小于180度),那么这两条直线在各自延长后,在内角和小于两个直角的一侧相交。
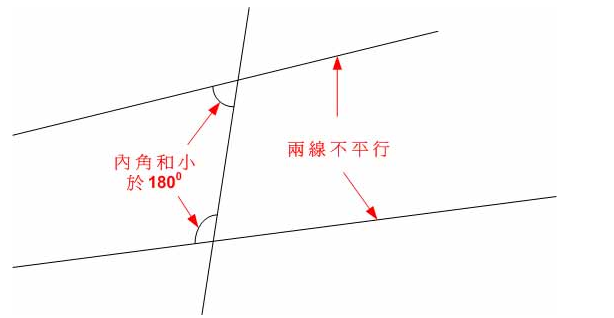
内角就是三线八角中的同旁内角。
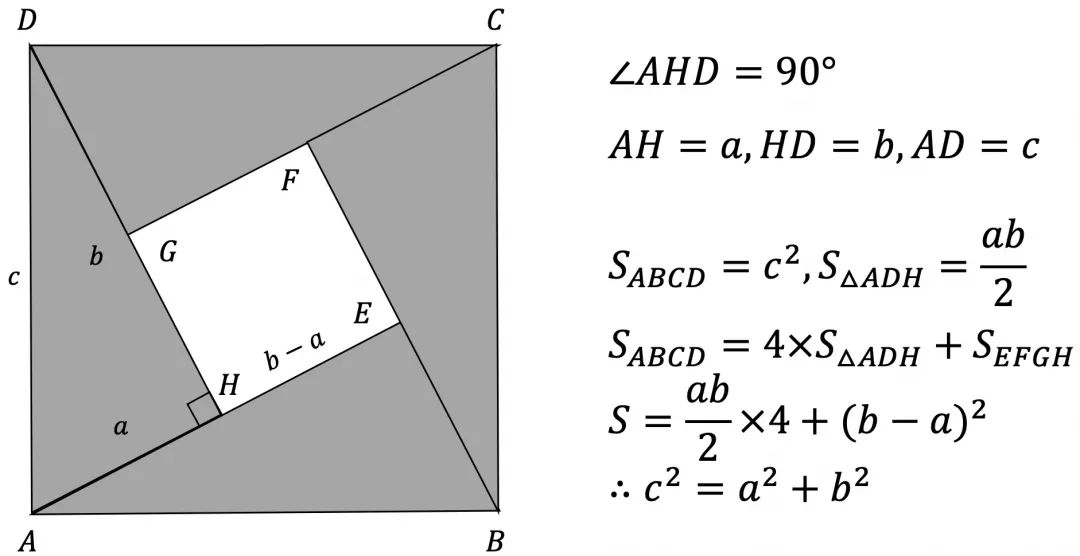
勾股定理的证明
经过一些系列的公理公设和众多定理的推演,我们得出了:$ c^2 = a^2 + b^2 $
标准化处理几何问题——向量
代数运算允许我们使用公式和算法来解决问题,而不依赖于直观的几何图形。这使得问题更容易被计算机处理,也更容易推广到更高维空间。
向量作为几何和代数之间的桥梁,通过坐标表示和运算规则,将几何问题转化为代数问题。
这种转换不仅简化了问题,还扩展了数学的应用范围,在现代工程中已经成为标准工具一般使用。
下面是用向量证明三角形中线命题。
用向量证明几何命题
利用向量几何的回路法来证明三角形的中位线等于底边长度的一半这一命题:
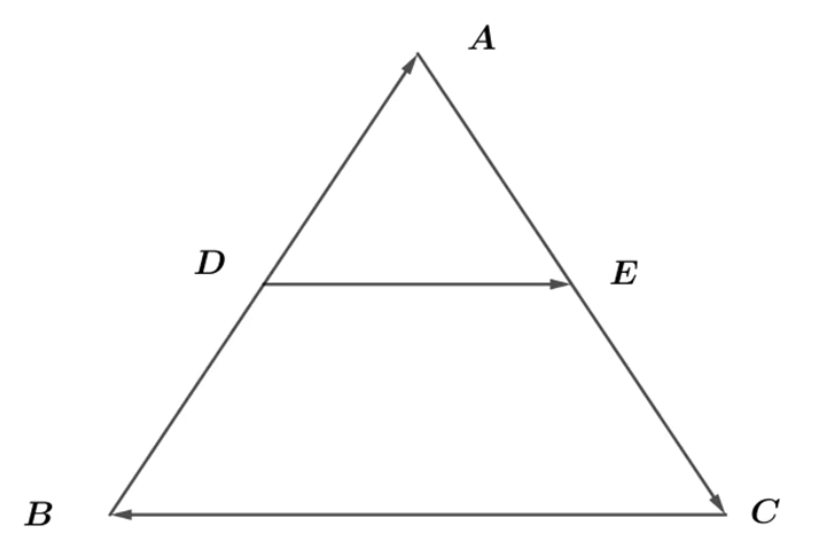
如果采用传统的几何图形画辅助线的方法还挺麻烦,向量法证明就很简单:
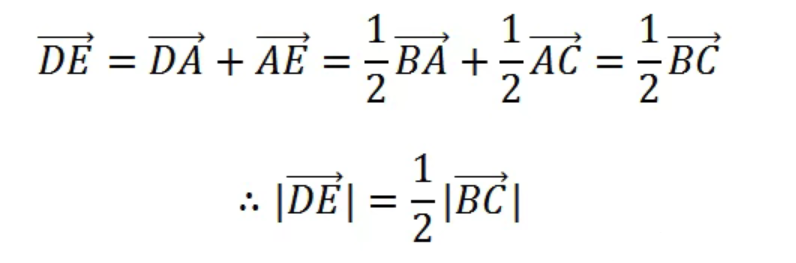
向量和复数的关联
todo

 浙公网安备 33010602011771号
浙公网安备 33010602011771号