二进制与位操作（位运算）

目录

• 一些基础概念
• 用二进制与十进制表示数
• 符号位与溢出
• 位操作
  • 向左移位 (<<)
  • 向右移位 (>>)
  • 位的或 (|)
  • 位的与 (&)
  • 位的异或 (^)
  • 位的取反 (~)
  • 位操作总结
  • 案例——按位与判断奇偶数
  • 案例——按位异或交换两个数字
    • 交换步骤：
  • 案例——集合的操作
    • 1. 并集（Union）
    • 2. 交集（Intersection）
    • 3. 差集（Difference）
    • 4. 对称差集（Symmetric Difference）
    • 5. 子集（Subset）和超集（Superset）
    • 位操作与集合操作的对比
  • 总结：
• Reference

---

都是一些很基础的东西，但总有一种历久弥新的感觉，所以还是想花点时间在做一次笔记。

一些基础概念

• 二进制与十进制的转换；
• 二进制的进位制度；
• 十六进制的进位制度；
• 负数、小数如何用二进制表示；
  • 符号位、溢出
  • 二进制的原码、反码、补码的认识
• 二进制数的运算；
• 二进制如何表示英文字符、符号；
• 二进制数如何表示各种编码的字符；

篇幅有限，这些概念就不展开介绍了，主要是解释下面的位操作，以及位操作的应用场景。

用二进制与十进制表示数

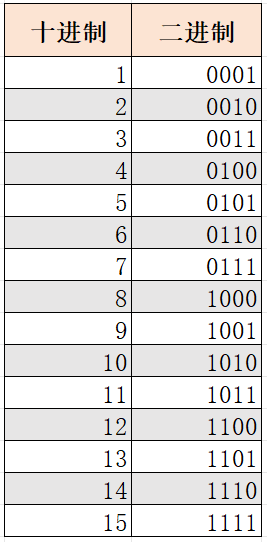
图1

符号位与溢出

符号位：
符号位是用于表示一个数的正负的二进制位。在计算机中，有符号数通常使用最高位作为符号位：

• 如果符号位是 0，表示该数为正数。
• 如果符号位是 1，表示该数为负数。

无符号数指最高位不是符号位，整体都是数字。

溢出：
溢出发生在运算结果超出数据类型所能表示的范围时。

假设我们使用8位有符号数（补码表示），范围是 -128 到 127。

1. 正溢出示例：

   • 计算 (100 + 50)：

     100: 01100100
     50:  00110010
     -------------
     150: 10010110  （二进制 `10010110` 是补码表示的 `-106`）
     

     • 正确结果应该是 150，但超出了8位有符号数的范围，实际结果为 -106。
     • 这是正溢出。

2. 负溢出示例：

   • 计算 (-100 - 50)：

     -100: 10011100
     -50:  11001110
     -------------
     -150: 01101010  （二进制 `01101010` 是补码表示的 `106`）
     

     • 正确结果应该是 -150，但超出了8位有符号数的范围，实际结果为 106。
     • 这是负溢出。

符号位与溢出的关系：
符号位在溢出判断中起着关键作用：

• 当两个正数相加时，如果结果的符号位变为 1，则说明发生了正溢出。
• 当两个负数相加时，如果结果的符号位变为 0，则说明发生了负溢出。

位操作

在计算机，一切操作最终都会转为二进制，然后再进行位运算操作，几乎所有的计算机语言都支持对二进制的位操作。

向左移位 (<<)

定义：将二进制数的所有位向左移动指定的位数，右侧空出的位用 0 填充。
描述：左移操作相当于将数乘以 (2^n)，其中 (n) 是移动的位数。
案例：

• 二进制数 5 的表示是 00000101。
• 左移 1 位后：00001010（即 10）。
• 左移 2 位后：00010100（即 20）。
• 公式：5 << 1 = 10，5 << 2 = 20。

---

向右移位 (>>)

定义：将二进制数的所有位向右移动指定的位数，左侧空出的位用符号位填充（正数补 0，负数补 1）。
描述：右移操作相当于将数除以 (2^n)，其中 (n) 是移动的位数（向下取整）。
案例：

• 二进制数 10 的表示是 00001010。
• 右移 1 位后：00000101（即 5）。
• 右移 2 位后：00000010（即 2）。
• 公式：10 >> 1 = 5，10 >> 2 = 2。

---

位的或 (|)

定义：对两个二进制数的每一位进行逻辑或操作，只要有一个位是 1，结果位就是 1。
描述：用于将某些位设置为 1。
案例：

• 二进制数 5 的表示是 00000101。
• 二进制数 3 的表示是 00000011。
• 按位或操作：00000111（即 7）。
• 公式：5 | 3 = 7。

---

位的与 (&)

定义：对两个二进制数的每一位进行逻辑与操作，只有当两个位都是 1 时，结果位才是 1。
描述：用于提取或保留某些位。
案例：

• 二进制数 5 的表示是 00000101。
• 二进制数 3 的表示是 00000011。
• 按位与操作：00000001（即 1）。
• 公式：5 & 3 = 1。

---

位的异或 (^)

定义：对两个二进制数的每一位进行逻辑异或操作，当两个位不同时，结果位是 1；相同时，结果位是 0。

异或（Exclusive OR，简称 XOR）运算可以通过数学符号“⊕”表示， 具有交换律、结合律、恒等律等性质。

描述：用于翻转某些位或比较两个数的差异。
案例：

• 二进制数 5 的表示是 00000101。
• 二进制数 3 的表示是 00000011。
• 按位异或操作：00000110（即 6）。
• 公式：5 ^ 3 = 6。

---

位的取反 (~)

定义：对一个二进制数的每一位进行逻辑取反操作，0 变为 1，1 变为 0。
描述：用于翻转所有位。
案例：

• 二进制数 5 的表示是 00000101。
• 按位取反操作：11111010（即 -6，在补码表示中）。
• 公式：~5 = -6。

---

位操作总结

• 左移 (<<) 和 右移 (>>) 用于快速乘以或除以 2 的幂。

• 位的或 (|) 用于设置某些位为 1。

• 位的与 (&) 用于提取或保留某些位。

• 位的异或 (^) 用于翻转某些位或比较差异。

• 位的取反 (~) 用于翻转所有位。

这些位操作在底层编程、加密算法、图像处理等领域有广泛应用，需要牢记。

---

案例——按位与判断奇偶数

2个步骤即可：

1. 将数字转换成二进制数；
2. 判断最后一位，为0是偶数，否则为奇数。

案例——按位异或交换两个数字

利用按位异或操作的性质，可以通过以下步骤交换两个变量 A 和 B值，而无需使用临时变量，达到节省资源的目的。

交换步骤：

实例演示：
假设 A = 5，B = 3。

1. 初始值：

   • (A = 5)（二进制：0101）
   • (B = 3)（二进制：0011）

2. 第一步：(A = A \oplus B)

   • (A = 5 \oplus 3)
   • 二进制计算：

     A: 0 1 0 1
     B: 0 0 1 1
     -----------
     A ^ B: 0 1 1 0  （二进制 `0110`，十进制 6）
     

   • 现在 (A = 6)，(B = 3)。
   • A 现在存储了A和B的差异。

3. 第二步：(B = A \oplus B)

   • (B = 6 \oplus 3)
   • 二进制计算：

     A: 0 1 1 0
     B: 0 0 1 1
     -----------
     A ^ B: 0 1 0 1  （二进制 `0101`，十进制 5）
     

   • 现在 (A = 6)，(B = 5)。
   • B 现在恢复为原来的A。

4. 第三步：(A = A \oplus B)

   • (A = 6 \oplus 5)
   • 二进制计算：

     A: 0 1 1 0
     B: 0 1 0 1
     -----------
     A ^ B: 0 0 1 1  （二进制 `0011`，十进制 3）
     

   • 现在 (A = 3)，(B = 5)。
   • A现在恢复为原来的B。

案例——集合的操作

集合操作用于处理一组不重复的元素，常见的集合操作包括并集、交集、差集和对称差集。

1. 并集（Union）

• 符号：| 或 union()
• 规则：包含两个集合中所有元素。
• 示例：

  A = {1, 2, 3}
  B = {3, 4, 5}
  result = A | B  # {1, 2, 3, 4, 5}
  

2. 交集（Intersection）

• 符号：& 或 intersection()
• 规则：仅包含两个集合中共同存在的元素。
• 示例：

  A = {1, 3, 8}
  B = {4, 8}
  result = A & B  # {8}
  

步骤演示：
假设我们给1到8的数字，编个编号 1-8，
如果某个数字在集合中，相应的位置为1，否则为0，
那么A集合 = 10000101，
B集合 = 10001000
result = A & B
result = {8}

3. 差集（Difference）

• 符号：- 或 difference()
• 规则：包含在第一个集合中但不在第二个集合中的元素。
• 示例：

  A = {1, 2, 3}
  B = {3, 4, 5}
  result = A - B  # {1, 2}
  

4. 对称差集（Symmetric Difference）

• 符号：^ 或 symmetric_difference()
• 规则：包含两个集合中非共同存在的元素。
• 示例：

  A = {1, 2, 3}
  B = {3, 4, 5}
  result = A ^ B  # {1, 2, 4, 5}
  

5. 子集（Subset）和超集（Superset）

• 子集符号：<= 或 issubset()
• 超集符号：>= 或 issuperset()
• 规则：判断一个集合是否是另一个集合的子集或超集。
• 示例：

  A = {1, 2}
  B = {1, 2, 3}
  is_subset = A <= B  # True
  is_superset = B >= A  # True
  

---

位操作与集合操作的对比

操作类型	位操作（二进制）	集合操作
与	&	&
或	`	`
异或	^	^
取反	~	无直接对应操作
左移/右移	<< / >>	无直接对应操作

总结：

• 计算机都是通过位操作直接操作二进制位，适合底层编程和性能优化，上述的案例也体现了其高效性；

• 按位操作是最节省资源的；

• 集合类操作适合做数据筛选；

• 位操作和集合操作在符号上有一定的相似性，但应用场景不同。只能说集合是基于位操作的。

Reference

《程序员的数学基础课》